目录
题目:
题目分析:
最后编写代码:
输出结果
题目:
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
感谢大佬的帮助:https://www.cnblogs.com/wangkundentisy/p/9378886.html
题目分析:
这是一题典型的DP问题。
1. 首先分析是否是DP问题,得满足两个条件:1.最优子结构;2.重叠子问题。
第n个骰子的点数实际上是在n-1这堆骰子的基础上进行的投掷。满足最优子结构
求父问题的时候多次用到子问题,想要解决第n个骰子的问题,需要前面的数据。满足重叠子问题
2.确定是DP问题之后,需要确定状态转移方程。
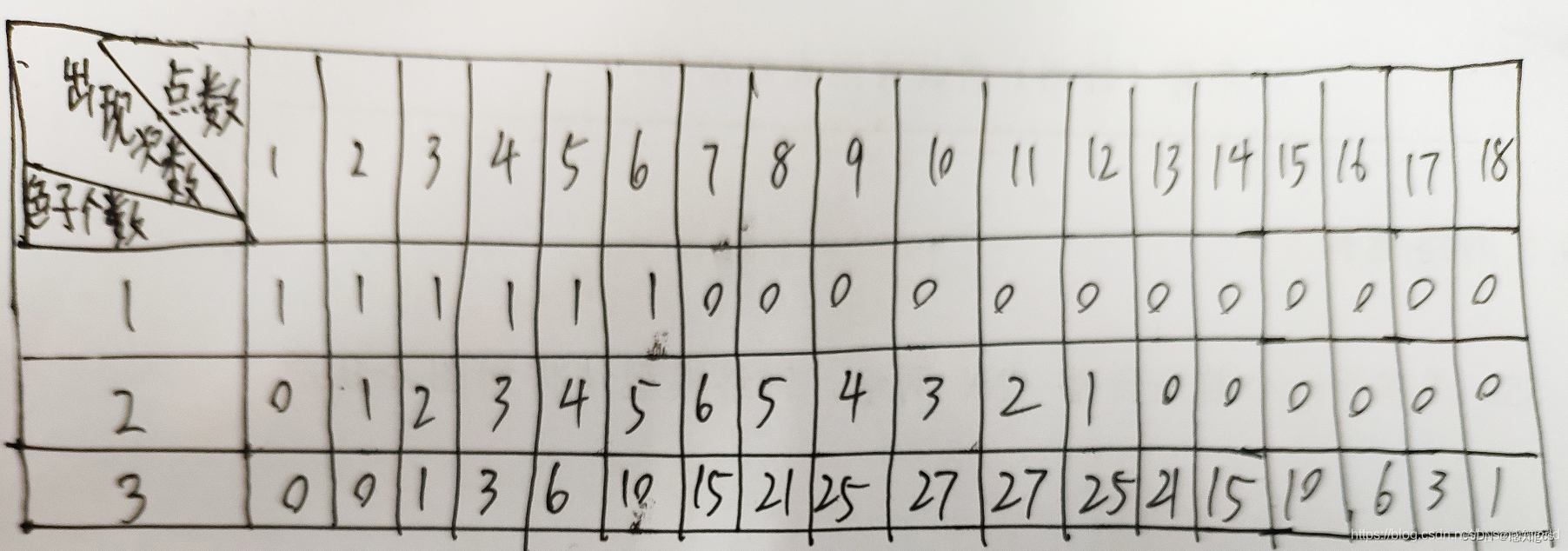
分析一下,第n个骰子的点数之和是与前面n-1那堆骰子的点数之和相关。其实情况还算蛮复杂的,光想是想不出来的,我们根据色子的投掷情况,列了下面表格,根据观察我们发现状态转换方程。我们不妨设f(n,k) = f(n-1,k-1) + f(n-1,k-2) + f(n-1,k-3) + f(n-1,k-4) + f(n-1,k-5) + f(n-1,k-6) ;这里n代表色子个数,k代表点数之和,f(n,k)代表n个色子投掷,点数之和为k的所有投掷次数。仔细想一下,第n个骰子投掷完之后的点数之和是不是等于上一次投掷点数次数之和,因为上一次有六种投法,所以要将这六种的可能次数都加起来。
3.在建立完状态方程之后,考虑将状态方程初始化,第一次投掷,1~6点数各自出现的次数都为1次吧,所以都初始化为1。
最后编写代码:
#include<iostream>
#include<math.h>
#include<vector>
using namespace std;class Solution {
public:vector<double> twoSum(int n) {vector<double> res;vector<vector<int> > dp(n + 1, vector<int>(n * 6 + 1, 0));//初始化for (int i = 1; i <= 6; i++){dp[1][i] = 1;}//填表int sum = 0;for (int i = 2; i <= n; i++){for (int j = i; j <= n * 6; j++){for (int k = 1; k <= 6; k++){if ((j - k) >= 0)//这里防止数组越界,看表就知道,数组会越界的dp[i][j] += dp[i - 1][j - k];elsebreak;}if (i == n){sum += dp[i][j];//直接计算n个色子投掷所有可能出现的次数总和}}}if (n == 1)sum = 6;for (int i = n; i <= n * 6; i++){res.push_back((double)dp[n][i] / sum);//用于计算概率,别忘记强制转换成double}return res;}
};
int main()
{Solution solution;vector<double> result = solution.twoSum(6);for (int j = 0; j <= result.size() - 1; j++){std::cout << result[j] << " ";}std::cout << "" << std::endl;return 0;
}
输出结果