机器学习系列文章
入门必读:机器学习介绍
文章目录
- 机器学习系列文章
- 前言
- 1. 感知机
- 1.1 感知机定义
- 1.2 感知机学习策略
- 2. 代码实现
- 2.1 构建数据
- 2.2 编写函数
- 2.3 迭代
- 3. 总结
前言
大家好,大家好✨,这里是bio🦖。这次为大家带来的是感知机模型。下面跟我一起来了解感知机模型吧!
感知机 (Perceptron) 是二类分类的线性分类模型 ,其输入为实例的特征向量 ,输出为实例的类别 ,分别为 +1 和 -1。1957年,由康奈尔航空实验室(Cornell Aeronautical Laboratory)弗兰克·罗森布拉特 (Frank Rosenblatt)提出。它可以被视为一种最简单形式的前馈神经网络,是一种二元线性分类器。在人工神经网络领域中,感知机也被指为单层的人工神经网络,以区别于较复杂的多层感知机。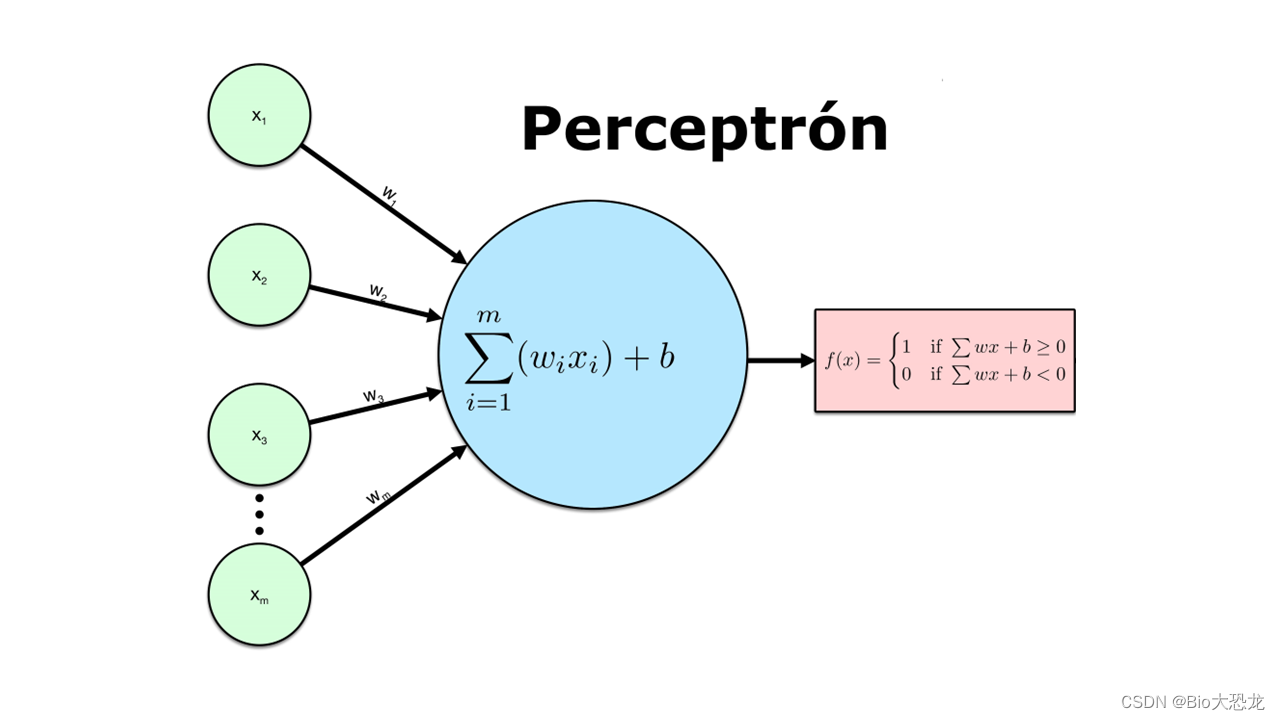
1. 感知机
1.1 感知机定义
感知器使用特征向量来表示二元分类器,把矩阵上的输入 x \mathcal{x} x(实数值向量)映射到输出值 y \mathcal{y} y 上(一个二元的值)。
f ( x ) = { + 1 , i f w ⋅ x + b > 0 − 1 , e l s e f(x) = \begin{cases} +1,\,\, if\,w\cdot x+b>0\\ -1,\,\,else\\ \end{cases} f(x)={+1,ifw⋅x+b>0−1,else
w \mathcal{w} w 是实数的表示权重的向量, w ⋅ x \mathcal{w} \cdot \mathcal{x} w⋅x 是点积。 b \mathcal{b} b 是偏置,一个不依赖于任何输入值的常数。
1.2 感知机学习策略
假设训练数据集是线性可分的 ,如下图所示。感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的直线 L \mathcal{L} L。 为了找出这样的超平而 , 即确定感知机模型参数 w \mathcal{w} w , b \mathcal{b} b ,需要确定一个学习策略 , 即定义损失函数并将损失函数极小化 。
损失函数的一个选择是误分类数据点的数量 。 但是这样的损失函数不是参数 w \mathcal{w} w , b \mathcal{b} b 的连续可导函数,不易优化 。 损失函数的另一个选择是误分类数据点到直线 L \mathcal{L} L 的总距离。感知机所采用的就是后者 。

- 对于错误分类的数据点 ( x i , y i ) (\mathcal{x_i, y_i}) (xi,yi),总有:
− y i ⋅ ( w ⋅ x i + b ) > 0 \mathcal{-y_i\cdot(w\cdot x_i+b) > 0} −yi⋅(w⋅xi+b)>0 - 错误分类点到直线 L \mathcal{L} L 的距离为:
1 ∥ w ∥ ∣ w ⋅ x i + b ∣ \mathcal{\frac{1}{\|w\|} \vert w \cdot x_i +b \vert} ∥w∥1∣w⋅xi+b∣ - 假设直线 L \mathcal{L} L 的误分类点集合为 m \mathcal{m} m , 那么所有误分类点到直线 L \mathcal{L} L 的总距离为:
− 1 ∥ w ∥ ∑ i m y i ⋅ ( w ⋅ x i + b ) \mathcal{-\frac{1}{\|w\|} \sum_{i}^{m}y_i\cdot(w \cdot x_i +b)} −∥w∥1i∑myi⋅(w⋅xi+b) - 不考虑 1 ∥ w ∥ \mathcal{\frac{1}{\|w\|}} ∥w∥1,感知机的损失函数为:
K ( w , b ) = − ∑ i m y i ⋅ ( w ⋅ x i + b ) \mathcal{K(w, b)= - \sum_{i}^{m}y_i\cdot(w \cdot x_i +b)} K(w,b)=−i∑myi⋅(w⋅xi+b)
显然,损失函数 K \mathcal{K} K 是非负的。如果没有误分类点,损失函数值是 0 。而且,误分类点越少,误分类点离超平面越近,损失函数值就越小 。
而感知机的优化算法采用的是随机梯度下降算法 (Stochastic Gradient Descent)(后续更新),用误分类数据驱动损失函数 K \mathcal{K} K 不断减小。本文将采取二维数据,来展示感知机的工作过程。
2. 代码实现
2.1 构建数据
首先创建二维数据,并用线性回归模型拟合出直线 L \mathcal{L} L。代码如下:
import numpy as np
from sklearn.datasets import make_classification
from sklearn import linear_model
import matplotlib.pyplot as plt
import random# two-dimention data
td_data = make_classification(n_samples=20, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=24)td_data = list(td_data)
td_data[1] = np.array([1 if i == 0 else -1 for i in td_data[1]])
td_data = tuple(td_data)# visualized data
fig, ax = plt.subplots()
scatter = ax.scatter(td_data[0][:, 0], td_data[0][:, 1], c=td_data[1], alpha=0.6, cmap="cool")
legend_1 = ax.legend(*scatter.legend_elements(), title="Classes", loc="upper left")
ax.add_artist(legend_1)
ax.set_xlabel("Feature_1")
ax.set_ylabel("Feature_2")# add minimal residual sum of squares line as gold standard
reg = linear_model.LinearRegression()# reshape for model fitting
reg.fit(td_data[0][:, 0].reshape(-1, 1), td_data[0][:, 1].reshape(-1, 1))
print(f"the intercept is {reg.intercept_[0]} and the coefficient is {reg.coef_[0][0]}")
formula = f"f(x)={round(reg.coef_[0][0], 2)}*x1-x2{round(reg.intercept_[0], 2)}"# create a x axis for plotting
create_x_axis = np.linspace(min(td_data[0][:, 0]), max(td_data[0][:, 0]), 100).reshape(-1, 1)
predicted_value = reg.predict(create_x_axis)ax.plot(create_x_axis, predicted_value, c="gold", alpha=0.8, label=formula)
handles, labels = ax.get_legend_handles_labels()
legend_2 = ax.legend(handles, labels, loc="lower right")plt.show()
根据代码输出的结果可知,由线性回归模型拟合出的直线 L = 0.53 x 1 + x 2 − 0.6 \mathcal{L = 0.53x_1+x_2-0.6} L=0.53x1+x2−0.6。

2.2 编写函数
接下来编写可复用的函数,减少代码编写量。partial_derivative_w 函数用于对变量 w \mathcal{w} w 求偏导,partial_derivative_b 函数用于对变量 b \mathcal{b} b 求偏导,decision_funtion 函数用于决策是否继续进行迭代,plot_function 函数绘制迭代结果图。
# take the partial derivative of w and b
def partial_derivative_w(data_point, label_point):# feature_1 * feature_2 * yresult_w_1 = data_point[0] * label_pointresult_w_2 = data_point[1] * label_pointreturn [result_w_1, result_w_2]def partial_derivative_b(label_point):# labelresult_b = label_pointreturn result_b# decision function. w and b will be change if exist data point make
def decision_funtion(weight_1, weigh_2, intercept):# if y*(w*x+b) < 0, the data point is wrongly classified.result = td_data[1] * ((td_data[0][:, 0] * weight_1) + (td_data[0][:, 1] * weight_2) + intercept)if len(result[np.where(result < 0)]) != 0:print(result)wrong_dp_index = np.where(result == result[np.where(result < 0)][0])[0][0]wrong_dp = td_data[0][wrong_dp_index]wrong_lb = td_data[1][wrong_dp_index]return [True, wrong_dp, wrong_lb]else:print("interation end")return [False, None, None]def plot_function(weight_1, weight_2, intercept):fig, ax = plt.subplots()scatter = ax.scatter(td_data[0][:, 0], td_data[0][:, 1], c=td_data[1], alpha=0.6)ax.legend(*scatter.legend_elements(), title="Classes")ax.set_xlabel("Feature_1")ax.set_ylabel("Feature_2")b = intercept/weight_2hyperplane = [(-(weight_1/weight_2) * i) - b for i in create_x_axis]ax.plot(create_x_axis, hyperplane, c='green', alpha=0.5)plt.show()
2.3 迭代
设置特征一的初始权重为 0,特征二的初始权重为 0,初始截距为 0,学习率为 0.1,迭代次数为1000次,随机从数据中选择一个数据点作为分类错误数据点后开始迭代。
# initiate weight, intercept and learning rate
weight_1 = 0
weight_2 = 0
intercept = 0
learn_rate = 0.1# iteration times
iteration_times = 1000# random value in two dimention data
random_index = random.randint(0, 19)
feature_point = td_data[0][random_index]
label_point = td_data[1][random_index]
# it is not correctly classified for any data point resulting in loss function equte 0.for iteration in range(iteration_times):# w1 = w0 + (learn_rate * y * x)new_weight_1 = weight_1 + (learn_rate * partial_derivative_w(feature_point, label_point)[0])new_weight_2 = weight_2 + (learn_rate * partial_derivative_w(feature_point, label_point)[1])# b1 = b0 + learn_rate * ynew_intercept = intercept + (learn_rate * partial_derivative_b(label_point))# decisiondecision_condition, wrong_dp, wrong_lp = decision_funtion(new_weight_1, new_weight_2, new_intercept)if decision_condition:weight_1 = new_weight_1weight_2 = new_weight_2intercept = new_intercept# wrong data pointfeature_point = wrong_dplabel_point = wrong_lpprint(f"The {iteration + 1} iteration\tweight_1={weight_1}\tweight_2={weight_2}\tintercept={intercept}\n")plot_function(weight_1, weight_2, intercept)else:print(f"The {iteration + 1} iteration\tweight_1={new_weight_1}\tweight_2={new_weight_2}\tintercept={new_intercept}\n")plot_function(new_weight_1, new_weight_2, new_intercept)break
迭代结果如下表所示,在迭代到第八次的时候,感知机模型成功将所有数据点正确分类。
| 迭代次数 | 效果图片 |
|---|---|
| 1 | 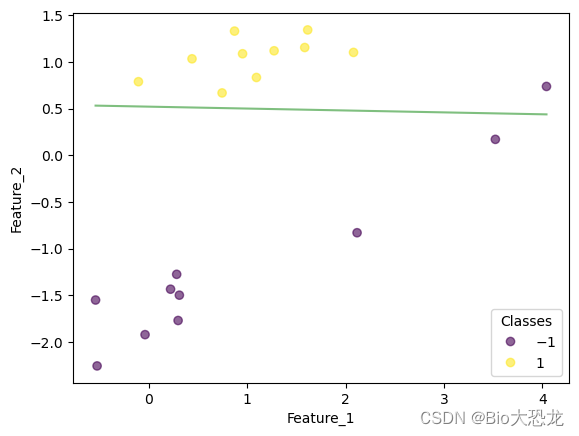 |
| 2 | 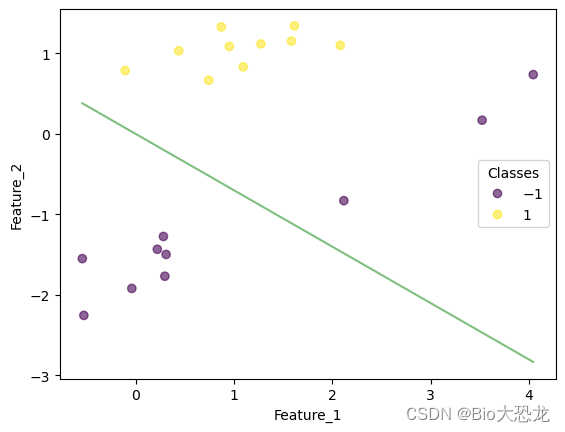 |
| 3 | 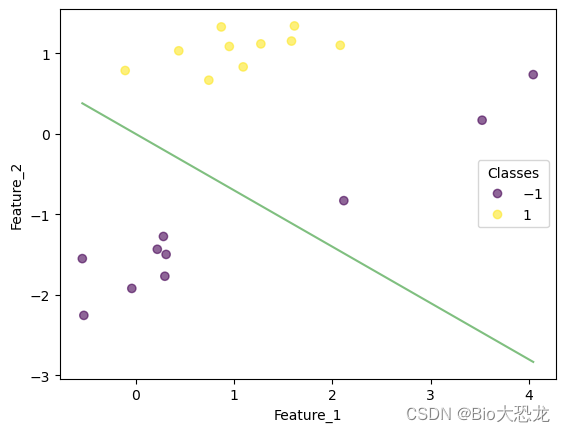 |
| 4 | 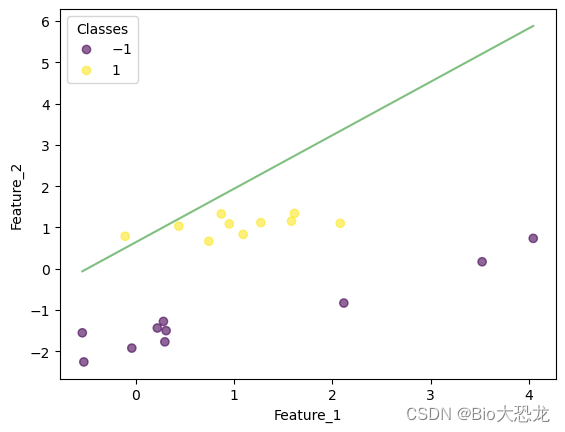 |
| 5 | 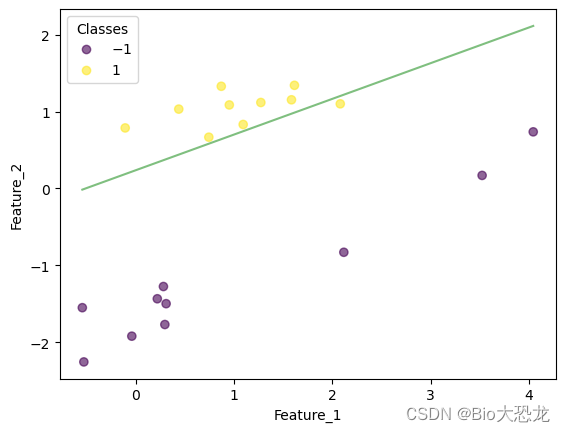 |
| 6 | 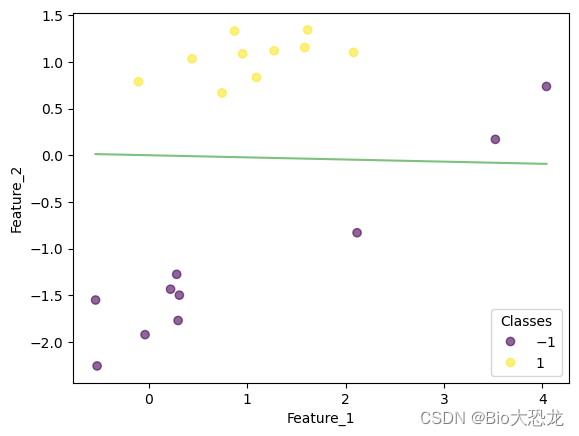 |
| 7 | 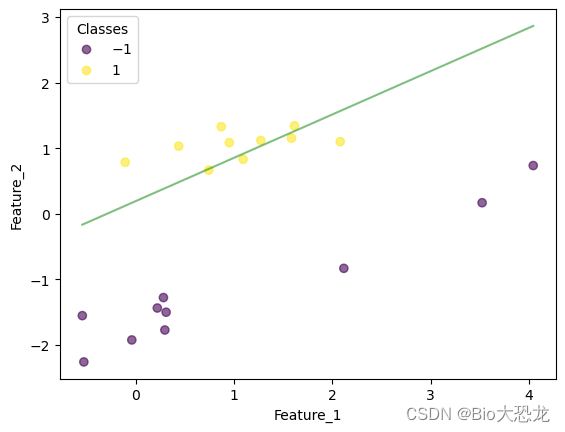 |
| 8 | 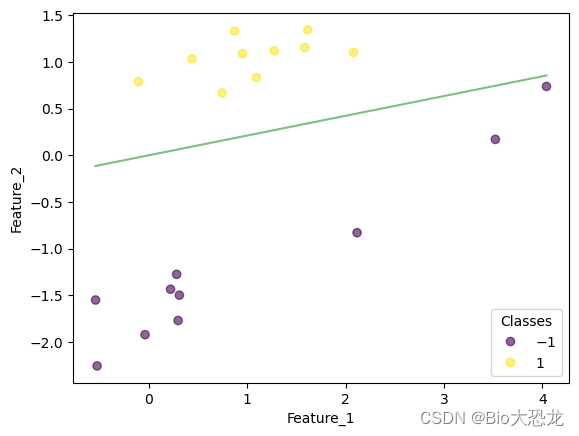 |
3. 总结
以上就是本次更新的全部内容。关于本次内容有一下缺点:
- 用于迭代的错误分类数据点没有被绘制出来。
- 由于跳过了大部分数学知识,内容衔接没有做好。
- 迭代数据点完全随机,复现过程可能不同。
后续将会更新:
- 感知机模型的数学解释
- 随机梯度算法的解释
- 可视化迭代过程的错误分类数据点(可能)
喜欢本次内容的小伙伴麻烦👍点赞+👍关注。