目录
- 一. 软间隔模型
- 1. 松弛因子的解释
- 小节
- 2. SVM软间隔模型总结
线性可分SVM中,若想找到分类的超平面,数据必须是线性可分的;但在实际情况中,线性数据集存在少量的异常点,导致SVM无法对数据集线性划分
也就是说:正常数据本身是线性可分的,但是由于存在异常点数据,导致数据集不能够线性可分
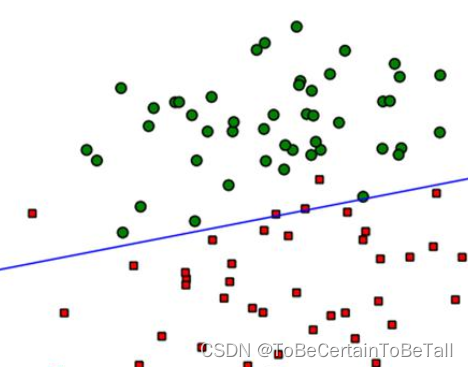
一. 软间隔模型
为了解决上述问题,我们引入软间隔的概念:
1. 松弛因子的解释
- 硬间隔: 线性划分SVM中的硬间隔是距离度量;在线性划分SVM中,要求函数距离一定是大于等于1的,最大化硬间隔条件为: { m i n 1 2 ∥ w → ∥ 2 s . t : y ( i ) ( ω T ⋅ x ( i ) + b ) ≥ 1 , i = 1 , 2 , . . . , m \left\{\begin{matrix}min\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2} \\s.t: y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1,i=1,2,...,m \end{matrix}\right. {min21 w 2s.t:y(i)(ωT⋅x(i)+b)≥1,i=1,2,...,m
- 软间隔:SVM对于训练集中的每个样本都引入一个松弛因子(ξ),使得函数距离加上松弛因子后的值是大于等于1; y ( i ) ( ω T ⋅ x ( i ) + b ) ≥ 1 − ξ ; i = 1 , 2 , . . . , m , ξ ≥ 0 y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1-\xi ;i=1,2,...,m,\xi\ge 0 y(i)(ωT⋅x(i)+b)≥1−ξ;i=1,2,...,m,ξ≥0
松弛因子(ξ)表示:相对于硬间隔,对样本到超平面距离的要求放松了
当 ξ = 0 ξ=0 ξ=0 , 相当于硬间隔
当 0 < ξ < 1 0<ξ<1 0<ξ<1 , 相当于样本点位于“街”内
当 ξ > 1 ξ>1 ξ>1 , 相当于样本点位于“街”对面
当 ξ > 2 ξ>2 ξ>2 , 相当于样本点位于“街”对面外侧注意: ξ ξ ξ只能对少量的样本起作用
ξ ξ ξ越大,表示样本点离超平面越近,
ξ > 1 ξ>1 ξ>1,那么表示允许该样本点分错因此:加入松弛因子是有成本的,过大的松弛因子可能会导致模型分类错误
所以,我们对存有异常点的数据集划分时,目标函数就变成了:
{ m i n 1 2 ∥ w → ∥ 2 + C ∑ i = 1 n ξ ( i ) y ( i ) ( ω T ⋅ x ( i ) + b ) ≥ 1 − ξ ( i ) , i = 1 , 2 , . . . , m \left\{\begin{matrix}min\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2}+C\sum_{i=1}^{n} \xi _{(i)} \\ \\y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1-\xi ^{(i)} ,i=1,2,...,m \end{matrix}\right. ⎩ ⎨ ⎧min21 w 2+C∑i=1nξ(i)y(i)(ωT⋅x(i)+b)≥1−ξ(i),i=1,2,...,m
ξ i ≥ 0 , i = 1 , 2 , . . . , m \xi{i}\ge 0,i=1,2,...,m ξi≥0,i=1,2,...,m
公式 C ∑ i = 1 n ξ ( i ) C\sum_{i=1}^{n} \xi _{(i)} C∑i=1nξ(i)表式:
每个样本惩罚项的总和不能大,函数中的C>0是惩罚参数,需要调参C越大,表示对错误分类的惩罚越大,也就越不允许存在分错的样本;
C越小表示对误分类的惩罚越小,也就是表示允许更多的分错样本存在也就是说:
对于完全线性可分的数据来说,C的值可以给大一点
对于线性可分但存在异常的数据来说,C的值需要调小
小节
对于线性可分的m个样本(x1,y1),(x2,y2)… :
x为n维的特征向量y为二元输出,即+1,-1
SVM的输出为w,b,分类决策函数
选择一个惩罚系数C>0,构造约束优化问题
{ min β ≥ 0 1 2 ∑ i = 1 m ∑ j = 1 m β i β j y ( i ) y ( j ) x ( j ) T x ( i ) − ∑ i = 1 m β i s . t : ∑ i = 1 m β i y ( i ) = 0 , 0 ≤ β i ≤ C , i = 1 , 2 , . . . , m \left\{\begin{matrix}\min_{\beta \ge 0}\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m} \beta _{i}\beta _{j} y^{(i)}y^{(j)}x^{(j)^{T}} x^{(i)}-\sum_{i=1}^{m} \beta _{i} \\s.t:\sum_{i=1}^{m} \beta _{i} y^{(i)}=0,0\le \beta _{i}\le C,i=1,2,...,m \end{matrix}\right. {minβ≥021∑i=1m∑j=1mβiβjy(i)y(j)x(j)Tx(i)−∑i=1mβis.t:∑i=1mβiy(i)=0,0≤βi≤C,i=1,2,...,m
使用SMO算法求出上述最优解 β \beta β
找到所有支持向量集合:
S = ( x ( i ) , y ( i ) ) ( 0 < β i < C , i = 1 , 2 , . . . , m ) S = (x^{(i)}, y^{(i)}) (0<\beta_{i} < C,i=1,2,...,m) S=(x(i),y(i))(0<βi<C,i=1,2,...,m)
从而更新w,b
w = ∑ i = 1 m β i x ( i ) y ( i ) w=\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} w=∑i=1mβix(i)y(i)
b = 1 S ∑ i = 1 S ( y s − ∑ i = 1 m β i x ( i ) T y ( i ) x s ) b=\frac{1}{S} \sum_{i=1}^{S}(y^{s}- \sum_{i=1}^{m} \beta _{i} x^{(i)^{T}}y^{(i)}x^{s} ) b=S1∑i=1S(ys−∑i=1mβix(i)Ty(i)xs)
构造最终的分类器,为:
f ( x ) = s i g n ( w ∗ x + b ) f(x)=sign(w\ast x+b) f(x)=sign(w∗x+b)
x<0时,y=-1x=0时,y=0x>0时,y=1注意:假设,不会出现0若出现,正负样本随意输出一个,即+0.00000001或-0.00000001都可以
2. SVM软间隔模型总结
可以解决线性数据中存在异常点的分类模型构建问题通过引入松弛因子,可以增加模型的泛化能力,即鲁棒性;对于模型而言:如果给定的惩罚项系数C越小,表示在模型构建的时候,就允许存在越多的分类错误的样本,也就表示此时模型的准确率会比较低;如果惩罚项系数越大,表示在模型构建的时候,就越不允许存在分类错误的样本,也就表示此时模型的准确率会比较高。
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
祝愉快🌟!