【并查集】一种简单而强大高效的数据结构

目录

一、并查集原理

二、并查集实现

三、并查集应用

1. LeetCode并查集相关OJ题

2. 并查集的其他应用及总结

一、并查集原理

并查集（Disjoint Set）是一种用来管理元素分组和查找元素所属组别的数据结构。它主要支持两种操作：查找（Find）和合并（Union）。

在并查集中，每个元素都被分配一个代表元素（也可以称为根节点），该代表元素用来表示所属的组别。初始时，每个元素都是其自身的代表元素，即根节点。当需要进行合并操作时，实际上是将两个组别的根节点连接在一起，从而将这两个组别合并为一个组别。而查找操作则是通过不断向上查找代表元素，直到找到根节点为止，以确定元素所属的组别。

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。

比如：某公司今年校招全国总共招生10人，西安招4人，成都招3人，武汉招3人，10个人来自不同的学校， 起先互不相识，每个学生都是一个独立的小团体，现给这些学生进行编号：{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，而现在它们对应的值就代表自身，即-1 （这里约定，每个下标对应值如果是非负数，代表这个下标属于这个值的集合，或者说这个值就是该下标的根；负数则代表是一个集合的根，且元素数量就为负号后的数字，具体的看后面的图对照） ; 给以下数组用来存储该小集体，数组中的数字代表：该小集体中具有成员的个数。此时假设同一个地方的学生分别组成了小分队，西安学生小分队s1={0,6,7,8}，成都学生小分队s2={1,4,9}，武汉学生小分队s3={2,3,5}就相互认识了，10个人形成了三个小团体。假设0,1,2担任队长，负责大家的出行。

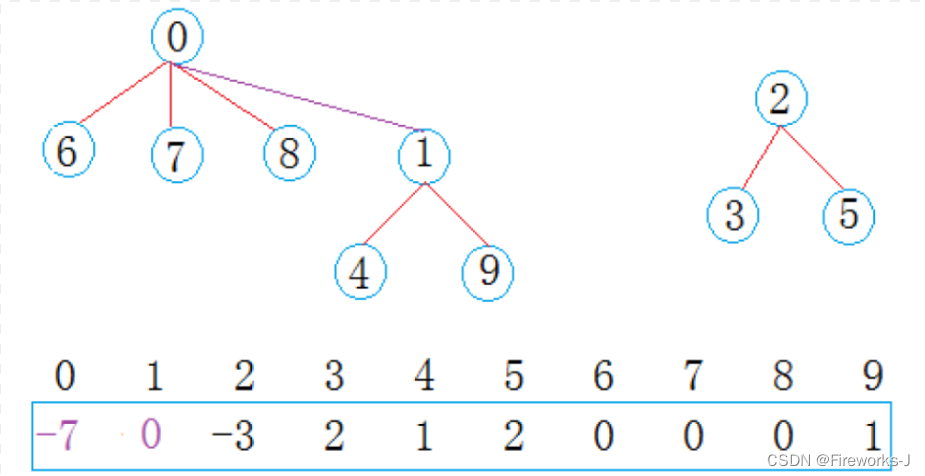
此时将这三个集合用一个数组表示：

从上图可以看出：编号6,7,8同学属于0号小分队，该小分队中有4人(包含队长0)；编号为4和9的同学属于1号小分队，该小分队有3人(包含队长1)，编号为3和5的同学属于2号小分队，该小分队有3个人(包含队长1)。

仔细观察数组，可以得出以下结论：
  1. 数组的下标对应集合中元素的编号
  2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
  3. 数组中如果为非负数，代表该元素双亲在数组中的下标

一段时间后，假设s1小分队的8号元素和s2小分队的1号元素玩到了一起，两个小圈子相互介绍认识，最后成为了一个小圈子，这就是合并。

现在0集合有7个人，2集合有3个人，总共两个朋友圈。

二、并查集实现

通过以上例子可知，并查集一般可以解决一下问题：
  • 1. 查找元素属于哪个集合
    • 沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)
  • 2. 查看两个元素是否属于同一个集合
    • 沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在
  • 3. 将两个集合归并成一个集合
    • 将两个集合中的元素合并
    • 将一个集合名称改成另一个集合的名称
  • 4. 集合的个数
    • 遍历数组，数组中元素为负数的个数即为集合的个数。

到此可以看到，并查集并不复杂。综上，就能够自己实现一个并查集：

import java.util.Arrays;public class UnionFindSet {public int[] elem;public UnionFindSet(int n) {this.elem = new int[n];Arrays.fill(elem, -1);}/*** 找x下标对应的根** @param x 下标* @return x根的下标*/public int findRoot(int x) {if (x < 0) {throw new IndexOutOfBoundsException("下标不合法");}while (elem[x] >= 0) {x = elem[x];}return x;}/*** 合并两个集合 x1和x2必须从根合并** @param x1 把x2作为自己的子集* @param x2 成为x1的子集*/public void union(int x1, int x2) {//x1和x2到自己集合的根位置x1 = findRoot(x1);x2 = findRoot(x2);if (x1 == x2) return; //相同根，不需要合并elem[x1] = elem[x1] + elem[x2];elem[x2] = x1;}/*** 判断两个下标对应的数字是否在一个集合中 -> 是否同根*/public boolean isSameSet(int x1, int x2) {x1 = findRoot(x1);x2 = findRoot(x2);return x1 == x2;}/*** 求数组中集合的个数*/public int getCount() {int count = 0;for (int x : elem) {if (x < 0) {count++;}}return count;}
}

UnionFindSet类测试： 

import java.util.Arrays;public class Test {public static void main(String[] args) {UnionFindSet ufs = new UnionFindSet(10);ufs.union(0, 6);ufs.union(0, 7);ufs.union(0, 8);ufs.union(1, 4);ufs.union(1, 9);ufs.union(2, 3);ufs.union(2, 5);System.out.println(Arrays.toString(ufs.elem));System.out.println("合并根为0和根为1的集合:");ufs.union(0, 1);System.out.println(Arrays.toString(ufs.elem));System.out.println(ufs.isSameSet(3, 6));System.out.println(ufs.isSameSet(4, 8));System.out.println(ufs.getCount());}
}

 测试结果正确：

三、并查集应用

1. LeetCode并查集相关OJ题

题目一：LeetCdoe 547. 省份数量icon-default.png?t=N7T8https://leetcode.cn/problems/number-of-provinces/description/

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

思路：前面我们已经自己实现了一个并查集，这里就可以用上。题目说到：isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。对于矩阵中值为1的元素，将他们所对应城市相连，进行合并（i ==j时就是自己和自己相连，不需要合并），最后看并查集中负数的个数，即为省份数量。

class Solution {public int findCircleNum(int[][] isConnected) {int n = isConnected.length;UnionFindSet ufs = new UnionFindSet(n);//遍历数组，合并for(int i = 0; i < n; i++) {for(int j = 0; j < isConnected[i].length; j++) {if(i != j && isConnected[i][j] == 1) {ufs.union(i, j);}}}return ufs.getCount();}
}

前面自己实现的并查集类也要放到代码框中，官方题解中同样有并查集的解法。

题目2：LeetCode 990. 等式方程的可满足性icon-default.png?t=N7T8https://leetcode.cn/problems/satisfiability-of-equality-equations/

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一："a==b" 或 "a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。 

思路：将每个变量看出一个节点，==关系看作两者的连接，即将两者合并成一个集合（题目的提示：出现的字母都为小写字母，因此集合的长度给26就够了）。我们先遍历一次数组，将所有==关系的变量合并；再遍历数组，看每个 != 关系的两个变量是否在同一个集合中，如果在同一个集合，说明与方程冲突，即为false。若都无冲突，即为true。

class Solution {public boolean equationsPossible(String[] equations) {//1.合并所有==的情况int n = equations.length;UnionFindSet ufs = new UnionFindSet(26);//所有小写字母for(int i = 0; i < n; i++) {if(equations[i].charAt(1) == '=') {//合并ufs.union(equations[i].charAt(0) - 'a',equations[i].charAt(3) - 'a');}}//2.判断!=的情况是否正确for(int i = 0; i < n; i++) {//如果==，说明不满足方程if(equations[i].charAt(1) == '!' && ufs.isSameSet(equations[i].charAt(0) - 'a',equations[i].charAt(3) - 'a')) {return false;}}return true;}
}

同样，前面自己实现的并查集类也要放到代码框中，官方题解中也是并查集的解法。

2. 并查集的其他应用及总结

并查集还有一些其他的应用：

  1. 连通性问题：并查集常被用来判断图中节点之间的连通性。通过并查集可以快速判断两个节点是否在同一个连通分量中，从而进行相关操作，比如最小生成树算法中的 Kruskal 算法。

  2. 图论中的环检测：在无向图中，可以利用并查集来检测是否存在环路。每次加入一条边时，如果边的两个端点已经在同一个连通分量中，则说明存在环路。

  3. 最近公共祖先（LCA）问题：在树形结构中，通过并查集可以快速计算两个节点的最近公共祖先。

  4. 社交网络中的关系处理：在社交网络中，可以利用并查集维护用户之间的关系，快速合并用户的关系圈子或者查找两个用户之间的关系。

总结：并查集在算法和数据结构领域有着广泛的应用，其时间复杂度通常为接近常数级别，使其成为许多算法和数据结构中重要的一部分。虽然并查集很优秀，但相对来说并查集面试的频率不是特别高，可以说不是一个面试热点。虽然如此，并查集的思想还是很实用的，是一个很有意思的数据结构，通常一旦想到用并查集解决问题，思路也会变得很清晰，所以建议还是好好学习一下。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/521052.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Chromium内核浏览器编译记（四）Linux版本CEF编译

Chromium内核浏览器编译记（四）Linux版本CEF编译

转载请注明出处&#xff1a;https://blog.csdn.net/kong_gu_you_lan/article/details/136508294 本文出自 容华谢后的博客 0.写在前面 本篇文章是用来记录编译Linux版本CEF的步骤和踩过的坑&#xff0c;以防止后续再用到的时候忘记&#xff0c;同时也希望能够帮助到遇到同样问…
阅读更多...
谷歌最新版本下载最新驱动网址chrome driver Version: 122.0.6261.111

谷歌最新版本下载最新驱动网址chrome driver Version: 122.0.6261.111

谷歌最新版本下载最新驱动网址chrome driver Version: 122.0.6261.111 https://googlechromelabs.github.io/chrome-for-testing/ 下载完之后放在谷歌安装路径下即可
阅读更多...
Prompt Engineering、Finetune、RAG：OpenAI LLM 应用最佳实践

Prompt Engineering、Finetune、RAG：OpenAI LLM 应用最佳实践

一、背景 本文介绍了 2023 年 11 月 OpenAI DevDay 中的一个演讲&#xff0c;演讲者为 John Allard 和 Colin Jarvis。演讲中&#xff0c;作者对 LLM 应用落地过程中遇到的问题和相关改进方案进行了总结。虽然其中用到的都是已知的技术&#xff0c;但是进行了很好的总结和串联…
阅读更多...
Ulysses for macOS v33.1 写作应用 兼容 M1/M2

Ulysses for macOS v33.1 写作应用 兼容 M1/M2

Ulysses 是面向 Mac、iPhone 和 iPad 的一站式写作环境。Ulysses 提供令人愉悦、专注的写作体验&#xff0c;加上高效文稿管理、无缝同步以及灵活导出&#xff0c;因此是各种写作人士的第一选择。 应用介绍 Ulysses 是面向 Mac、iPhone 和 iPad 的一站式写作环境。Ulysses 提供…
阅读更多...
大数据冷热分离方案

大数据冷热分离方案

数据冷热分离方案 1、背景 ​ 随着业务的发展&#xff0c;在线表中的数据会逐渐增加。常规业务都有冷热数据现象明显的特性&#xff08;需要访问的都是近期产生的热数据&#xff1b;时间久远的冷数据出于备份、备案溯源等诉求会进行在线保留&#xff09;。在业务表数据 量可控…
阅读更多...
react tab选项卡吸顶实现

react tab选项卡吸顶实现

react tab选项卡吸顶实现&#xff0c;直接上代码&#xff08;代码有注释&#xff09; tsx代码 /* eslint-disable react-hooks/exhaustive-deps */ import React, { useEffect, useState } from "react"; import DocumentTitle from react-document-title import s…
阅读更多...
java操作内存，简单讲解varhandle的使用

java操作内存，简单讲解varhandle的使用

概述&#xff1a;按理说jdk8的unsafe类就够用了&#xff0c;估计是因为不安全的原因&#xff0c;到jdk9出了个varhandle类&#xff0c;到jdk21的时候出了Arena和MemorySegment,基本就可以取代unsafe类的使用了。这里我主要讲varhandle类&#xff0c;因为大部分人升级jdk顶多升到…
阅读更多...
网页在特殊日子一键变灰

网页在特殊日子一键变灰

<template> <div :class"{ grayscale: isGrayscale }"> <!-- 你的页面内容放在这里 --> </div> </template> <script> export default { data() { return { // 存储哀悼日的数组 aidaoriDates:["0404", &q…
阅读更多...
使用Pytorch导出自定义ONNX算子

使用Pytorch导出自定义ONNX算子

在实际部署模型时有时可能会遇到想用的算子无法导出onnx&#xff0c;但实际部署的框架是支持该算子的。此时可以通过自定义onnx算子的方式导出onnx模型&#xff08;注&#xff1a;自定义onnx算子导出onnx模型后是无法使用onnxruntime推理的&#xff09;。下面给出个具体应用中的…
阅读更多...
pytorch续写tensorboard

pytorch续写tensorboard

模型训练到一半有 bug 停了&#xff0c;可以 resume 继续炼&#xff0c;本篇给出 pytorch 在 resume 训练时续写 tensorboard 的简例&#xff0c;参考 [1-3]&#xff0c;只要保证 writer 接收的 global step 是连着的就行。 Code import numpy as np from torch.utils.tensor…
阅读更多...
【节能减排/能耗分析/设备运维】AcrelEMS-Zone园区能源管理系统解决方案

【节能减排/能耗分析/设备运维】AcrelEMS-Zone园区能源管理系统解决方案

市场规模 智慧园区市场稳步增长&#xff0c;市场规模由2019年的1191亿元增至2021年的1394亿元。智慧园区作为产业升级转型的重要载体&#xff0c;近年来受到国家政策大力支持&#xff0c;行业前景广阔&#xff0c;预计2022年智慧园区市场规模将达1543亿元&#xff0c;2024年市…
阅读更多...
如何让JMeter也生成精美详细allure测试报告

如何让JMeter也生成精美详细allure测试报告

&#xff08;全文约2000字&#xff0c;阅读约需5分钟&#xff0c;首发于公众号&#xff1a;测试开发研习社&#xff0c;欢迎关注&#xff09; 内容目录&#xff1a; 一、需求 二、思路 三、验证 四、实现 五、优化 六、彩蛋 篇幅较长&#xff0c;建议先收藏后阅读 一、需…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023