在做数据分析类的产品功能设计时,经常用到可视化方式,挖掘数据价值,表达数据的内在规律与特征展示给客户。
可是作为一个产品经理,(1)如果不能够掌握各类可视化图形的含义,就不知道哪类数据该用哪个图形。光知道可视化图形的含义还不够,(2)还要掌握该类可视化图形需要的后台数据结构是怎样的,才能指导数据处理人员或后端开发在现有数据结构的基础上,处理数据,供各类可视化图形调用。
下面,将以腾讯的数据可视化API为案例,学习可视化图形的原理,方便后续正确使用这些图形,进行数据可视化表达。如果有理解错误的地方,欢迎大家及时反馈,避免误导他人,多谢啦。
散点图
散点图可以用不同的颜色,用以展示海量数据点的分布情况。

散点图的属性
styles:定义各类点的样式。
值是DotCircleStyle对象,如下:
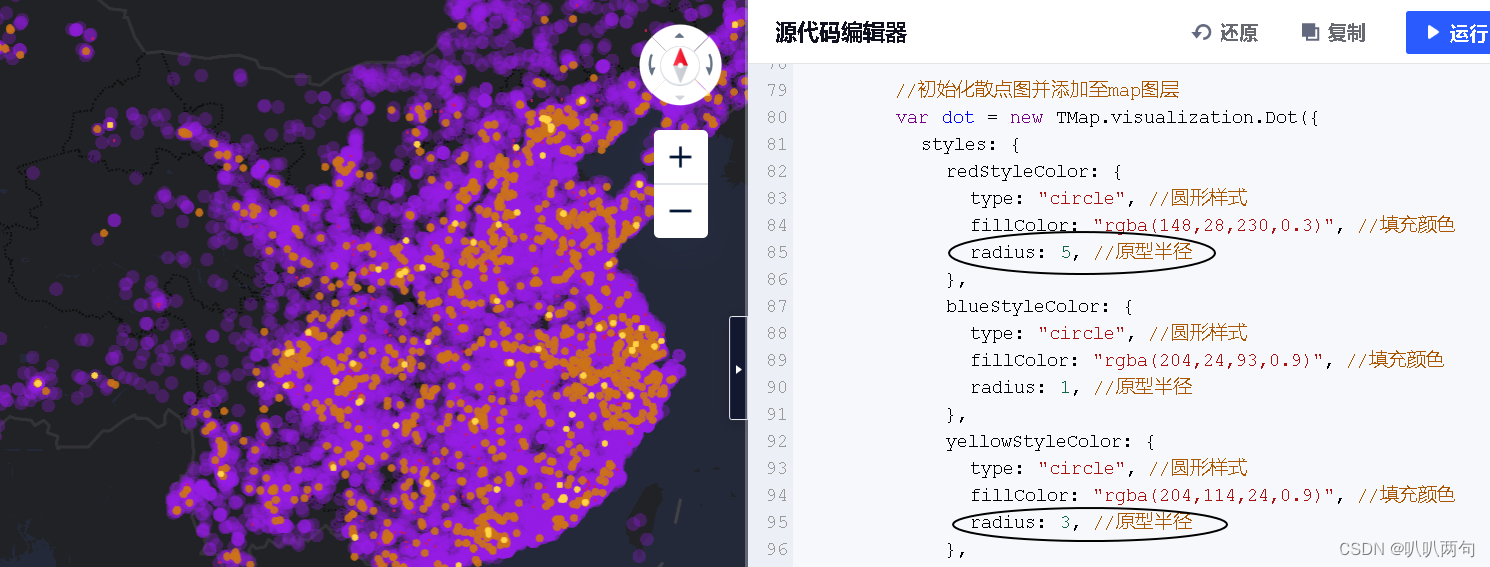
//初始化散点图并添加至map图层var dot = new TMap.visualization.Dot({styles: {redStyleColor: {type: "circle", //圆形样式fillColor: "rgba(148,28,230,0.3)", //填充颜色radius: 5, //原型半径},blueStyleColor: {type: "circle", //圆形样式fillColor: "rgba(204,24,93,0.9)", //填充颜色radius: 1, //原型半径},yellowStyleColor: {type: "circle", //圆形样式fillColor: "rgba(204,114,24,0.9)", //填充颜色radius: 3, //原型半径},greenStyleColor: {type: "circle", //圆形样式fillColor: "#FFD343", //填充颜色strokeWidth: 0, //边线宽度radius: 2.5, //原型半径},},});
DotCircleStyle对象的属性
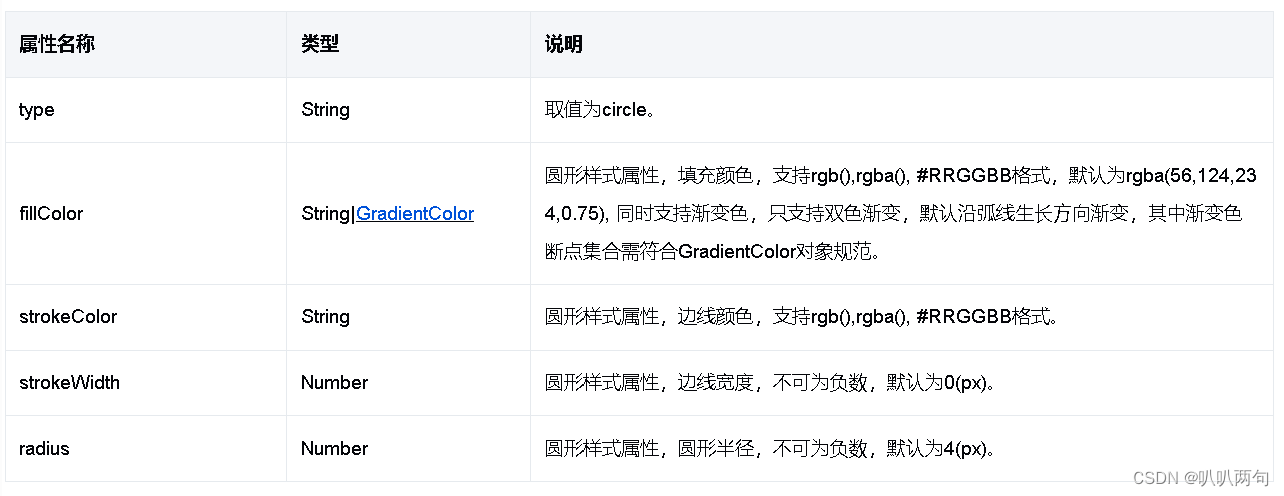
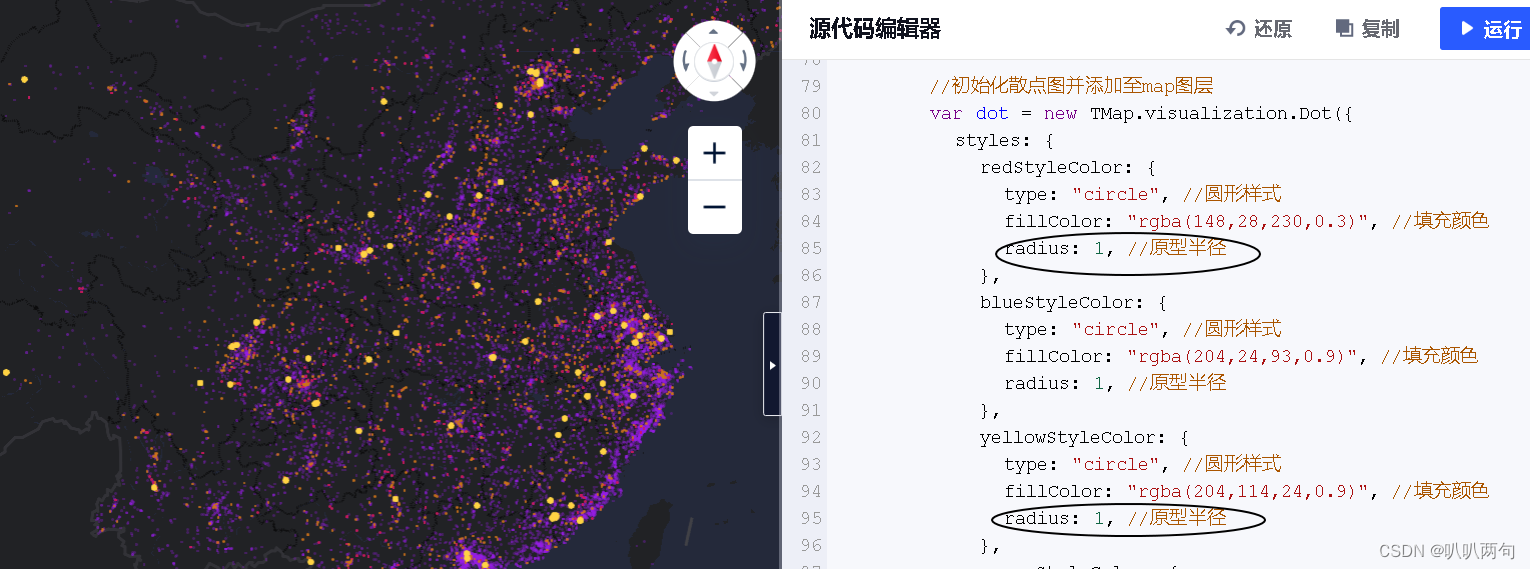
分类散点图的数据结构。
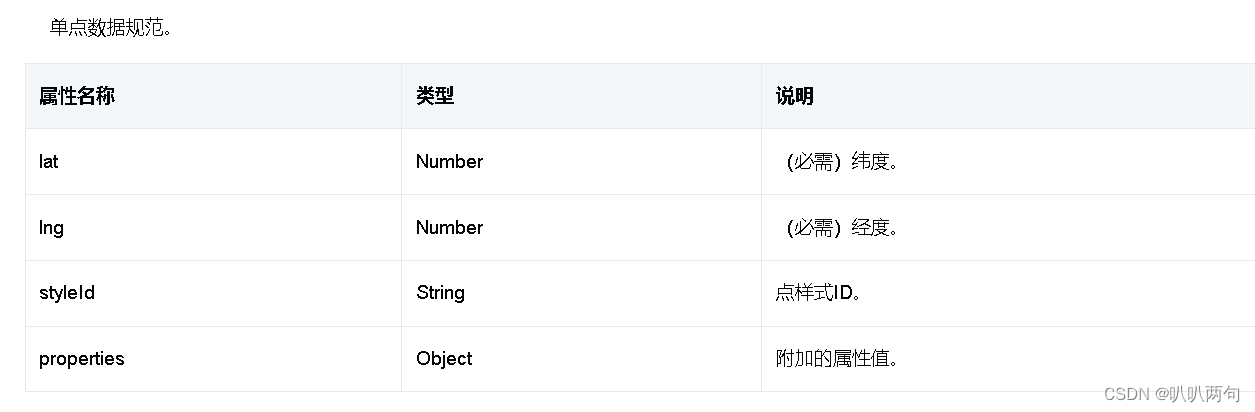
后台返回的数据结构如下:
{"lat":40.291213,"lng":116.217873,"Level":1}
{"lat":36.2101309,"lng":120.6078105,"Level":1}
{"lat":41.29751081,"lng":124.0801604,"Level":1}
{"lat":18.3103549,"lng":109.4774275,"Level":2}
{"lat":41.79905,"lng":86.3628,"Level":2}
{"lat":29.654266,"lng":91.118541,"Level":2}
{"lat":33.130101,"lng":113.73093,"Level":2}
{"lat":47.10542785,"lng":120.4911804,"Level":2}
{"lat":31.701024,"lng":119.924692,"Level":1}
{"lat":39.36467,"lng":109.807,"Level":1}
{"lat":40.9989318,"lng":117.9291109,"Level":1}
{"lat":25.70453,"lng":100.14331,"Level":1}
{"lat":29.587624,"lng":119.025671,"Level":1}
{"lat":25.0204019,"lng":117.6898475,"Level":1}
{"lat":36.27128,"lng":111.675826,"Level":1}
{"lat":21.56940085,"lng":111.8472104,"Level":1}
{"lat":27.6932899,"lng":117.1576515,"Level":1}
{"lat":36.67523225,"lng":117.0257111,"Level":1}
{"lat":34.21274,"lng":108.97435,"Level":4}
{"lat":34.2212,"lng":108.96412,"Level":4}
{"lat":29.6502848,"lng":91.1333369,"Level":4}
{"lat":29.747517,"lng":105.796243,"Level":4}
{"lat":25.01840081,"lng":113.7281004,"Level":4}
其中,level是自定义的业务属性,前端人员根据这个值,指定每个点的样式styleId,样式从styles属性里选择对应的样式。
//对点数据进行分类,并设置styleIddotSortData.forEach(function (item, index) {if (level == 1) {item.styleId = "greenStyleColor";} else if (level == 2) {item.styleId = "yellowStyleColor";} else if (level == 3) {item.styleId = "blueStyleColor";} else {item.styleId = "redStyleColor";}});