贡献法的核心在于,分析每个元素对答案的贡献。
1.孤独的照片
4261. 孤独的照片 - AcWing题库

最暴力的做法是枚举出所有情况,时间复杂度是O(),显然会超。
我们用贡献法的方式来思考。
对于某一头牛,假设它为G牛,它的左边距离上一头G牛的间隔为l,右边距离下一头G牛的间隔为r,那么它可以贡献出l*r+(l-1)+(r-1)张孤独的照片。l*r表示在G牛左右都有牛,左边有l(选1头牛、2头牛......l头牛)种可选的情况,右边有r(选1头牛、2头牛......r头牛)种可选的情况;(l-1)表示G牛只有左边有牛,这时有(l-1)种(2头牛、3头牛......l头牛)可选的情况,右边同理。
分析完贡献后,我们的结果就是每一头牛对答案的贡献之和。
#include<iostream>
using namespace std;
const int N=5e5+10;
typedef long long ll;
int n;
char a[N];
int l[N],r[N];
int main()
{scanf("%d",&n);scanf("%s",a+1);for(int i=1,h=0,g=0;i<=n;i++){if(a[i]=='H') l[i]=g,g=0,h++;else if(a[i]=='G') l[i]=h,h=0,g++;}for(int i=n,h=0,g=0;i>=1;i--){if(a[i]=='H') r[i]=g,g=0,h++;else if(a[i]=='G') r[i]=h,h=0,g++;}ll res=0;for(int i=1;i<=n;i++){res+=(ll)l[i]*r[i];if(l[i]>=2) res+=l[i]-1;if(r[i]>=2) res+=r[i]-1;}printf("%lld",res);
}2.子串分值
2868. 子串分值 - AcWing题库

同样地,我们分析每个元素对结果的贡献。
对于某个元素来说,假设它离上一个与它相同的元素距离为l,离下一个与它相同的元素距离为r,那么它的贡献应该是(l+1)*(r+1)。
对于这道题来说,我们处理l和r是不那么容易的,因为元素的种类很多,但是我们可以处理元素左右离它最近的相同元素的位置,假设左边是l,右边是r,当前元素是k,那么左边的个数是(k-l-1+1)=k-l,右边是r-k。
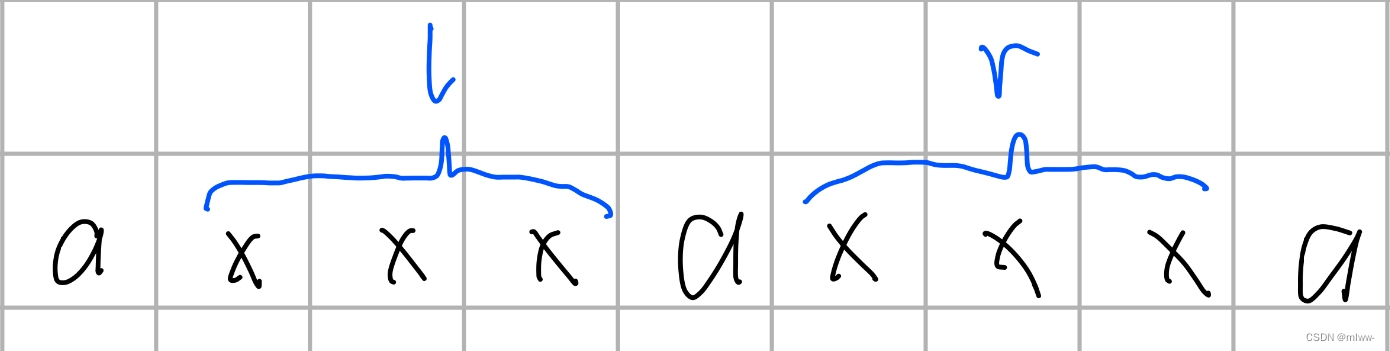
这里还需要注意一下边界,如果当前元素左边没有相同元素,我们默认l=0,如果右边没有相同元素,默认r=n+1。
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10;
typedef long long ll;
char a[N];
int l[N],r[N];
int last[N];
int main()
{scanf("%s",a+1);int n=strlen(a+1);for(int i=1;i<=n;i++){int cur=a[i]-'a';l[i]=last[cur];last[cur]=i;}for(int i=0;i<30;i++) last[i]=n+1;for(int i=n;i>=1;i--){int cur=a[i]-'a';r[i]=last[cur];last[cur]=i;}ll res=0;for(int i=1;i<=n;i++) {res+=(ll)(i-l[i])*(r[i]-i);}printf("%lld",res);
}3.牛的基因学
5154. 牛的基因学 - AcWing题库

对于示例TCG和GCA来说,假设我们固定了TCG,只移动GCA,那么,GCA中的G必须会与TCG中的G配对1次,GCA中的C必须会和TCG中的C配对一次。
同理,当GCA移动到CAG、AGC时,情况一样。
因此在移动过程中,最大总次数是2*3=6。
我们来看一组新的样例TTCG和GCAT,假设固定了TTCG,只移动GCAT,我们可以发现,GCAT中的T一定会和TTCG中的T配对2次,T一定会配对一次,C一定会配对一次。
因此在移动过程中,最大总次数是(2+1+1)*3=12.
也就是说,我们的最大总次数只和字母在s中出现的次数有关。
即:如果GCAT变为GCTT,则最大总次数是(2+2+1+1)*3=18.
对我们来说,t数组是可以自行构造的,要达到真正的最大总次数,我们应该使t数组的组成元素和s数组中出现次数最多的元素一致。
也就是说,如果s数组中出现次数最多的元素有1个,那t数组的每个元素只有1种选择,最后的答案是,如果s数组种出现次数最多的元素有2个,那么t数组的每个元素有2种选择,最后的答案是
,以此类推,就可以解出我们的题目了。
#include<iostream>
#include<unordered_map>
#include<algorithm>
using namespace std;
const int N=1e5+10;
typedef long long ll;
int n;
char a[N];
int cnt[5];
unordered_map<char,int> ha;
const int mod=1e9+7;
bool cmp(int x,int y)
{return x>y;
}
int main()
{scanf("%d",&n);scanf("%s",a+1);ha['A']=1;ha['G']=2;ha['C']=3;ha['T']=4;for(int i=1;i<=n;i++)cnt[ha[a[i]]]++;sort(cnt+1,cnt+1+4,cmp);int num=1;int maxx=cnt[1];for(int i=2;i<=4;i++) if(cnt[i]==maxx) num++;ll res=1;for(int i=1;i<=n;i++){res*=num;res%=mod;}printf("%lld",res);
}