前言
LQR全称Linear Quadratic Regulator(线性二次调节器),顾名思义用于解决形如
x ˙ = A x + B u y = C x + D u \begin{aligned}\dot{x}&=Ax+Bu\\y&=Cx+Du\end{aligned} x˙y=Ax+Bu=Cx+Du
线性时不变系统的一种线性控制方法,是最优控制方法的一种。
LQR通过全状态反馈将不同状态加权求和得到最优控制量,本文所讨论的是无限时间LQR问题,即可以保证系统是渐进稳定的,不考虑收敛时间。该方法主要思想是构造以状态量以及控制量相关的二次代价函数,通过最小化该代价函数寻找成本最低的解。
LQR基本原理
考虑形如
x ˙ = A x + B u y = C x + D u \begin{aligned}\dot{x}&=Ax+Bu\\y&=Cx+Du\end{aligned} x˙y=Ax+Bu=Cx+Du的系统
其中控制量满足
u = − K x u=-Kx u=−Kx
K为反馈矩阵
考虑无穷时间内的代价函数,由于系统无稳态误差,故时间趋于无穷时终端约束项为0
构造代价函数为
m i n J = 1 2 ∫ 0 ∞ ( x T Q x + u T R u ) d t , Q = Q T , R = R T , Q ≥ 0 , R > 0 min J=\frac1{2}\int_0^\infty(x^TQx+u^TRu)dt,Q=Q^T,R=R^T,Q\geq0,R>0 minJ=21∫0∞(xTQx+uTRu)dt,Q=QT,R=RT,Q≥0,R>0
一般地,Q和R均为正定对角阵。
求解该代价函数最小时所对应的K矩阵,即可求得最优控制量。
matlab中可以直接使用工具包求解,如
K=lqr(A,B,Q,R)
公式推导
利用拉格朗日乘子法构造增广泛函
J , = ∫ 0 ∞ ( 1 2 ( x T Q x + u T R u ) + λ T ( A x + B u − x ˙ ) ) d t J^{,}=\int_0^\infty(\frac1{2}(x^TQx+u^TRu)+\lambda^T(Ax+Bu-\dot{x}))dt J,=∫0∞(21(xTQx+uTRu)+λT(Ax+Bu−x˙))dt
定义纯量函数,及哈密尔顿函数
H ( x , u , λ , t ) = 1 2 ( x T Q x + u T R u ) + λ T ( A x + B u ) H(x,u,\lambda,t)=\frac1{2}(x^TQx+u^TRu)+\lambda^T(Ax+Bu) H(x,u,λ,t)=21(xTQx+uTRu)+λT(Ax+Bu)
则有
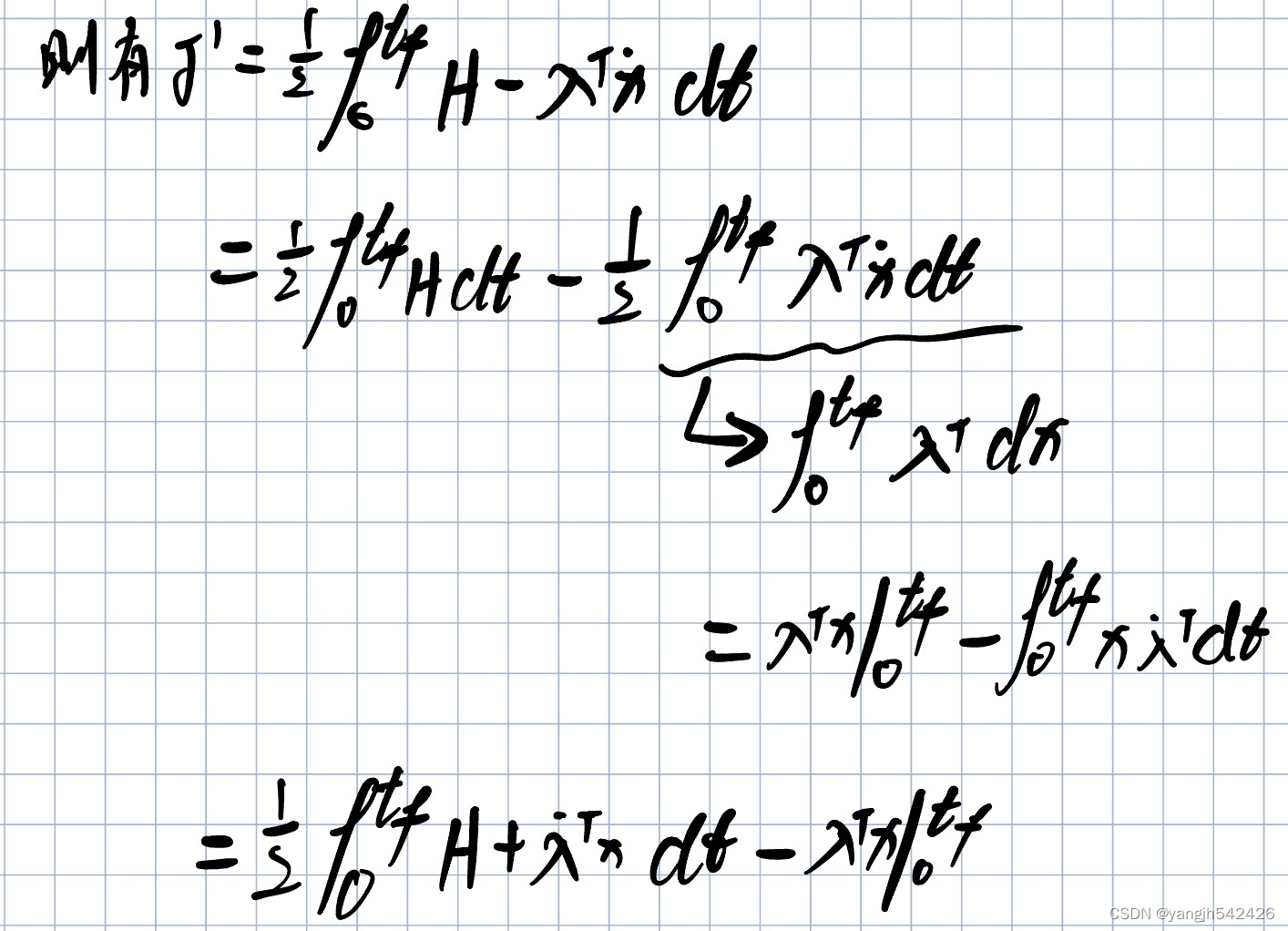
由变分法可得取极值时应满足控制方程
∂ H ∂ u = 0 \frac{\partial H}{\partial u}=0 ∂u∂H=0
则有
∂ H ∂ u = R u + B T λ = 0 \frac{\partial H}{\partial u}=Ru+B^T\lambda=0 ∂u∂H=Ru+BTλ=0
得
u ∗ = − R − 1 B T λ u^*=-R^{-1}B^T\lambda u∗=−R−1BTλ
又u应为关于x得线性表达,且由上式可得此时u为 λ \lambda λ的线性表达,故 λ \lambda λ也应为x的线性表达。
设
λ = P x \lambda=Px λ=Px
则有
u ∗ = − R − 1 B T P x u^*=-R^{-1}B^TPx u∗=−R−1BTPx
又根据正则方程
∂ H ∂ x + λ ˙ = 0 \frac{\partial H}{\partial x}+\dot\lambda=0 ∂x∂H+λ˙=0
∂ H ∂ λ = x ˙ \frac{\partial H}{\partial \lambda}=\dot x ∂λ∂H=x˙
得
λ ˙ = − ∂ H ∂ x = − Q x − A T λ = − Q x − A T P x \dot\lambda = -\frac{\partial H}{\partial x} = -Qx-A^T\lambda=-Qx-A^TPx λ˙=−∂x∂H=−Qx−ATλ=−Qx−ATPx
x ˙ = ∂ H ∂ λ = A x − B R − 1 B T P x \dot x=\frac{\partial H}{\partial \lambda}=Ax-BR^{-1}B^TPx x˙=∂λ∂H=Ax−BR−1BTPx
又对 λ = P x \lambda=Px λ=Px两边求导,得
λ ˙ = P ˙ x + P x ˙ \dot\lambda=\dot Px+P\dot x λ˙=P˙x+Px˙
P为常数矩阵时,则有
− Q x − A T P x = P A x − P B R − 1 B T P x -Qx-A^TPx = PAx-PBR^{-1}B^TPx −Qx−ATPx=PAx−PBR−1BTPx
又x为非零矩阵,则有
P A + A T P − P B R − 1 B T P + Q = 0 PA+A^TP-PBR^{-1}B^TP+Q=0 PA+ATP−PBR−1BTP+Q=0
即为riccati方程
求解该方程可得P
由此可解得 u ∗ = − R − 1 B T P x u^*=-R^{-1}B^TPx u∗=−R−1BTPx
仿真
在上篇基础上进行控制器修改
TODO