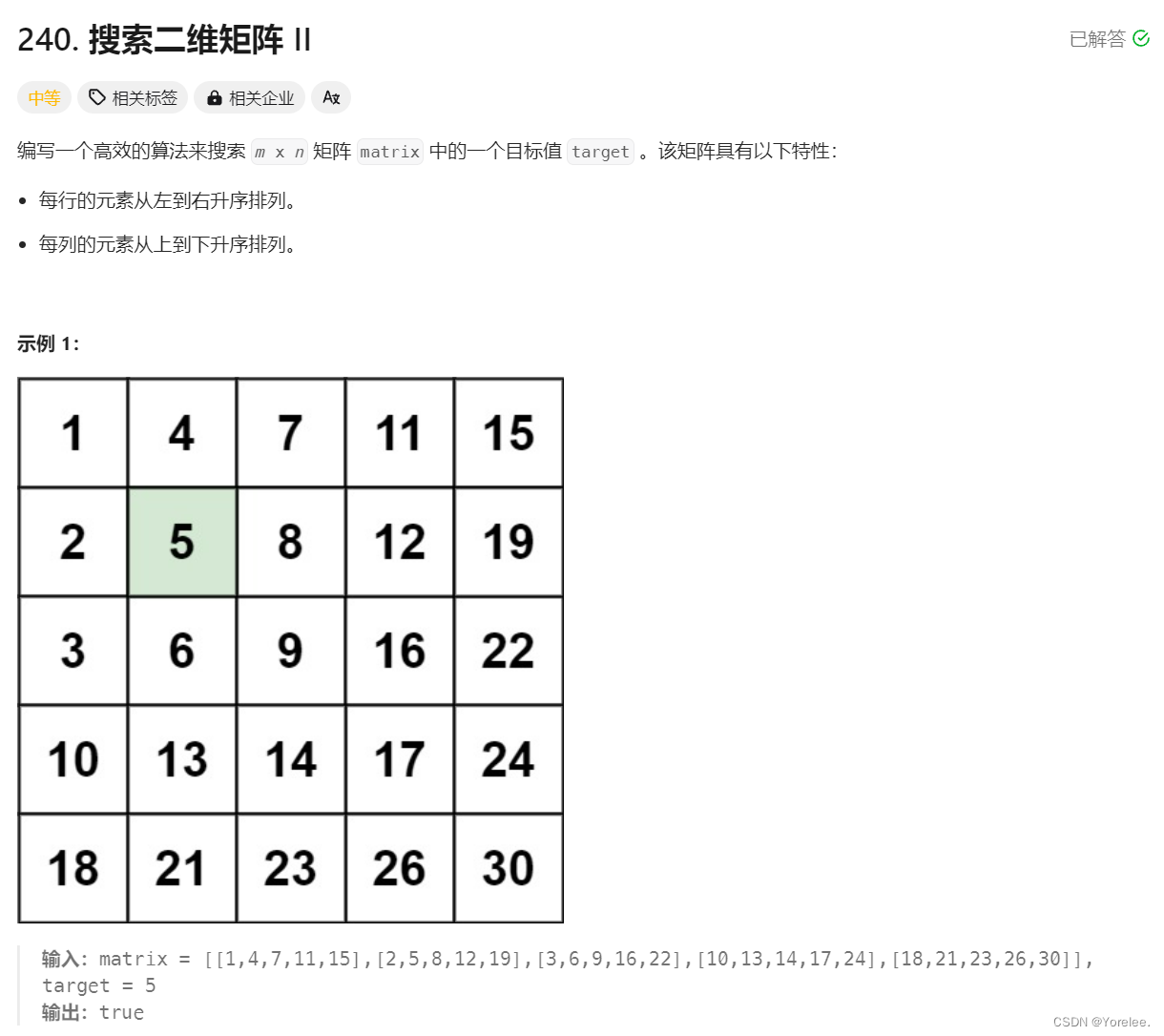
吉大21级算法分析与设计的一道大题，由于每一行都是排好序的直接逐行二分 可以达到：O(mlogn)。但是这里追求更广的思路可以使用其他方法。

矩阵四分：

在矩阵中用中心点比较，如果target大于中心点的值，则由于升序排列，以中心点为右下角的小矩阵就不用再查找了，因为他们一定比target小。剩下三个矩形都可能比中心点大，因此在剩下三个矩阵中继续查找；如果target小于中心点，以中心点为右下角的小矩阵可能包含，并且中心点的左下方和右上方都有可能比中心点小，因此仍然需要继续查找。

        每次可以去掉矩阵中的¼，对于每一个小矩阵它们是整个矩阵的¼，分析如下：

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {tar=target;return find(matrix,0,matrix.size()-1,0,matrix[0].size()-1);}
private:bool find(vector<vector<int>>& matrix,int row_left,int row_right,int col_top,int col_bottom){if(row_left>row_right||col_top>col_bottom||col_bottom>=matrix[0].size()||row_right>=matrix.size()) return false;if(row_left==row_right&&col_top==col_bottom&&tar!=matrix[row_left][col_bottom]) return false;int mid_row=(row_left+row_right)>>1;int mid_col=(col_top+col_bottom)>>1;if(tar==matrix[mid_row][mid_col]) return true;if(tar>matrix[mid_row][mid_col])return find(matrix,mid_row+1,row_right,col_top,mid_col)||find(matrix,row_left,mid_row,mid_col+1,col_bottom)||find(matrix,mid_row+1,row_right,mid_col+1,col_bottom);else return find(matrix,row_left,mid_row,col_top,mid_col)||find(matrix,mid_row+1,row_right,col_top,mid_col)||find(matrix,row_left,mid_row,mid_col+1,col_bottom);}
private:int tar;
};

Z字形查找：

Krahets - 力扣（LeetCode）：

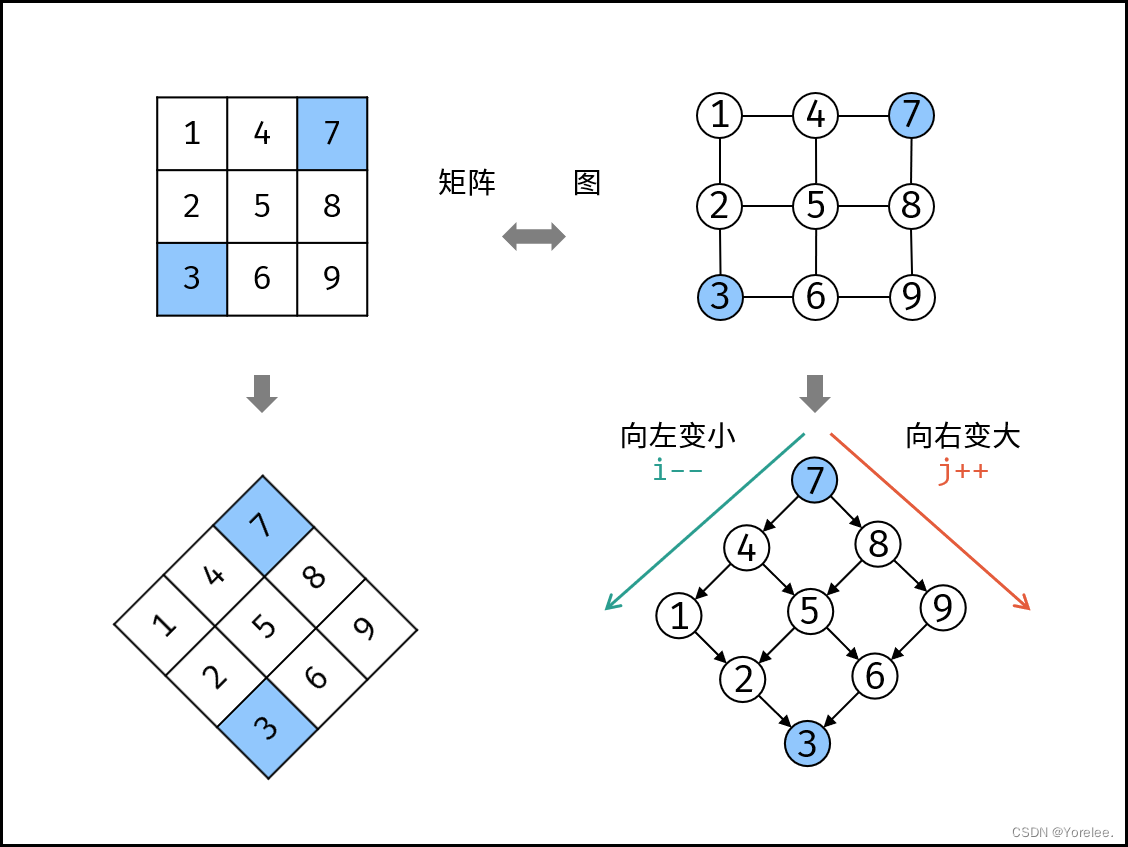
用二叉树来看就特别清晰了。任何一个结点均满足，左儿子小于它，右儿子大于它。如果target比它大，同一行左边一定不再满足要求，如果target比它小，同一列下边一定不再满足要求。由于我们是从右上角开始的，依次进行，每一步都使得解只能在划定的范围内，因此这样做是正确的，时间复杂度为O(m+n)。

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m=0,n=matrix[0].size()-1;while(m<matrix.size()&&n>=0&&matrix[m][n]!=target){if(matrix[m][n]>target) --n;else ++m;}cout<<m<<' '<<n;if(m<matrix.size()&&n>=0) return true;return false;}
};

暴力解法：

防止题目做多了不会暴力了（）

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {for(int i=0;i<matrix.size();++i)for(int &num:matrix[i])if(num==target) return true;return false;}
};