动态规划DP之背包问题3---多重背包问题-编程知识

动态规划DP之背包问题3---多重背包问题

DP分析：

优化：

二进制优化

例题：

01背包是每个物品只有一个，完全背包问题是每个物品有无限个。

那么多重背包问题就是 每个物品有有限个。

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

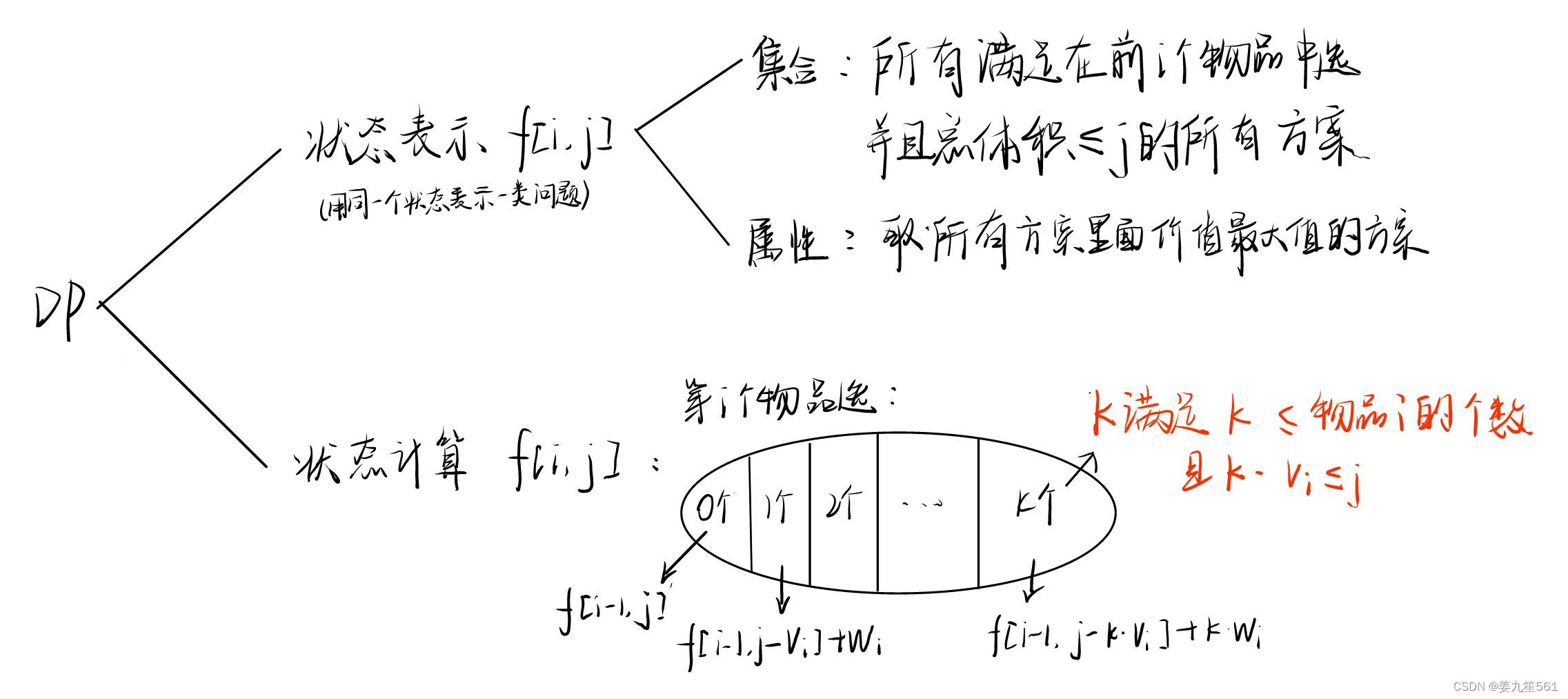
DP分析：

和完全背包问题很像，暴力算法都是多加一层循环，循环物品的个数。O(n^3)

动态规划DP之背包问题2---完全背包问题-CSDN博客

实现代码：

for(int i=1;i<=n;i++){for(int j=1;j<=V;j++){f[i][j] = f[i-1][j];for(int k=0;k<=s[i]&&k*v[i]<=j;k++)f[i][j] = Math.max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);                    }
}

优化：

不能采用完全背包的优化方式。动态规划DP之背包问题2---完全背包问题-CSDN博客

因为：

$f[i,j]=max(f[i-1,j],f[i-1,j-v]+w,...\ f[i-1,j-sv]+sw)$

$f[i,j-v]=max(\ f[i-1,j-v],f[i-1,j-2v]+w,...\ f[i-1,j-sv]\\+(s-1)w,\ f[i-1,j-(s+1)v]+sw)$

多了一个 $f[i-1,j-(s+1)v]+sw$ ，而max是不能减少一个获取到最大值的。

二进制优化

和快速幂的思路方法很像。快速幂（求解原理+例题）-CSDN博客

假如：物品 $i$ 的数量为 $s_i=1023$

暴力做法就是从 $1$ 枚举到 $1023$ 。
使用二进制优化，我们只需要枚举 $(int)(log_2s_i)+1$ 个数： $1,2,4,8,16,...512$ ，就可以组合出 $[0,1023]$ 中的任意一个整数。（相当于二进制表示转化为十进制）

一般性下，如和求出 $s_i\ log$ 下需要的数是哪些：

$2^0,\ 2^1,\ 2^2,\ 2^3,\ ...2^k, \ c\ \ (c=s_i-2^0-2^1-...2^k,\ c<2^{k+1})$

从 $2^0$ 到 $2^k$ 可以组合成 $[0,2^{k+1}-1]$ 之间的任何一个数，加上 $c$ 后可以组成 $[c,2^{k+1}-1+c]$ ，其中 $2^{k+1}-1+c = s_i$ 。

如何保证第一段 $[0,2^{k+1}-1]$ 与 $[c,2^{k+1}-1+c]$ 之间没有空隙，即 $2^{k+1}-1$ 是否大于 $c$ 。

因为 $c$ 的取值 $c<2^{k+1}$ 保证了：

$2^0+2^1+2^2+2^3+ ...2^k+ 2^{k+1} >s_i\\2^0+2^1+2^2+2^3+ ...2^k\ \ \ \ \ \ \ \ \ \leqslant s_i\\ 2^0+2^1+2^2+2^3+ ...2^k+ \ c \ \ \ =s_i$

如果 $c>=2^{k+1}$ ，那么就会取 $2^{k+1}$ ，不是 $c$ 了。

因此，我们将 $s_i\rightarrow logs_i$ ，然后针对分开后的所有物品使用01背包处理方式。时间复杂度降为 $O(n^2logs)$ 。

优化代码：

转换为01背包问题，将 $s_i$ 拆后的所有数，分别作为一种物品的数量。

for(int i=1;i<=n;i++){str = in.readLine().split(" ");int vi = Integer.parseInt(str[0]); // 物品i的体积int wi = Integer.parseInt(str[1]); // 物品i的价值int si = Integer.parseInt(str[2]); // 物品i的数量// 直接将该物品数目拆分成多个，但是拆分完后的物品数目可以组合成si中的任何一个数目int k = 1; // 从1开始划分，每次乘23while(si>=k){ //满足c<2^(k+1) ，即是s大于k，才能划分k个物品出去v[cnt] = vi*k; // 个数*体积，作为新一个物品w[cnt] = wi*k;si -= k; // 减去划分的k *= 2; cnt++;}if(si!=0){ // 最后剩下的物品，即cv[cnt] = si*vi;w[cnt] = si*wi;cnt++;}
}
n = cnt;

例题：

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N≤1000
0<V≤2000
0<vi,wi,si≤2000

提示：

本题考查多重背包的二进制优化方法。

输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例：
10

import java.io.*;
import java.util.*;class Main{static int N = 20010;static int n,V;static int[] v = new int[N]; // 体积static int[] w = new int[N]; // 价值static int[] s = new int[N]; // 个数static int[] f = new int[N]; // 二维会超内存public static void main(String[] args) throws IOException{BufferedReader in = new BufferedReader(new InputStreamReader(System.in));String[] str = in.readLine().split(" ");n = Integer.parseInt(str[0]);V = Integer.parseInt(str[1]);int cnt = 1;for(int i=1;i<=n;i++){str = in.readLine().split(" ");int vi = Integer.parseInt(str[0]);int wi = Integer.parseInt(str[1]);int si = Integer.parseInt(str[2]);// 直接将该物品数目拆分成多个，但是拆分完后的物品数目可以组合成si中的任何一个数目int k = 1;while(si>=k){ //满足c<2^(k+1) ，则是s大于k，才能划分k个物品出去v[cnt] = vi*k;w[cnt] = wi*k;si -= k;k *= 2;cnt++;}if(si!=0){ // 最后剩下的物品v[cnt] = si*vi;w[cnt] = si*wi;cnt++;}}n = cnt;// 转化为01背包问题for(int i=1;i<n;i++)for(int j=V;j>=v[i];j--)f[j] = Math.max(f[j],f[j-v[i]]+w[i]);                      System.out.println(f[V]); }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/522414.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！