前言
递推最通俗的理解就是数列,递推和数列的关系就好比 算法 和 数据结构 的关系,数列有点像数据结构中的顺序表,而递推就是一个循环或者迭代的枚举过程。
递推本质上是数学问题,所以有同学问算法是不是需要数学非常好,也并不是,你会发现,这些数学只不过是初中高中我们学烂的东西,高考都经历了,这些东西又何足为惧!?
一、斐波那契数列
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1,给定 n(0 ≤ n ≤ 30) ,请计算 F(n) 。

拿到这个题目,我们首先来看题目范围, 最多不超过 30,那是因为斐波那契数的增长速度很快,是指数级别的。所以如果 n 很大,就会超过 c语言 中32位整型的范围。这是一个最基础的递推题,递推公式都已经告诉你了,我们要做的就是利用一个循环来实现这个递推。
我们只需要用一个 F[31] 数组,初始化好 F[0] 和 F[1],然后按照给定的公式循环计算就可以了。像这样:
int fib(int n) {
int i; // (1)
int F[31] = {0, 1}; // (2)
for(i = 2; i <= n; ++i) { // (3)
F[i] = F[i-1] + F[i-2]; // (4)
}
return F[n]; // (5)
}
- (1) 首先定义一个循环变量;
- (2) 再定义一个数组记录斐波那契数列的第 n 项,并且初始化第 0 项 和 第 1 项。
- (3) 然后一个 for 循环,从第 2 项开始;
- (4) 利用递推公式逐步计算每一项的值;
- (5) 最后返回第 n 项即可。
二、泰波那契数列
泰波那契序列 Tn 定义如下:
T(0) = 0, T(1) = 1, T(2) = 1
且在 n > 2 的条件下 T(n) = T(n-1) + T(n-2) + T(n-3),给你整数 n,请返回第 n 个泰波那契数 T(n) 的值。
如果已经理解斐波那契数列,那么这个问题也不难,只不过初始化的时候,需要初始化前三个数,并且在循环迭代计算的时候,当前数的值需要前三个数的值累加和。像这样:
int tribonacci(int n){
int T[100];
T[0] = 0;
T[1] = 1;
T[2] = 1;
for(int i = 3; i <= n; ++i) {
T[i] = T[i-1] + T[i-2] + T[i-3];
}
return T[n];
}
三、斐波那契数列变形
给定一个 n(1 ≤ n ≤ 45) 代表总共有 n 阶楼梯,一开始在第 n 阶,每次可以爬 1 或者 2 个台阶,问总共有多少种不同的方法可以爬到楼顶。
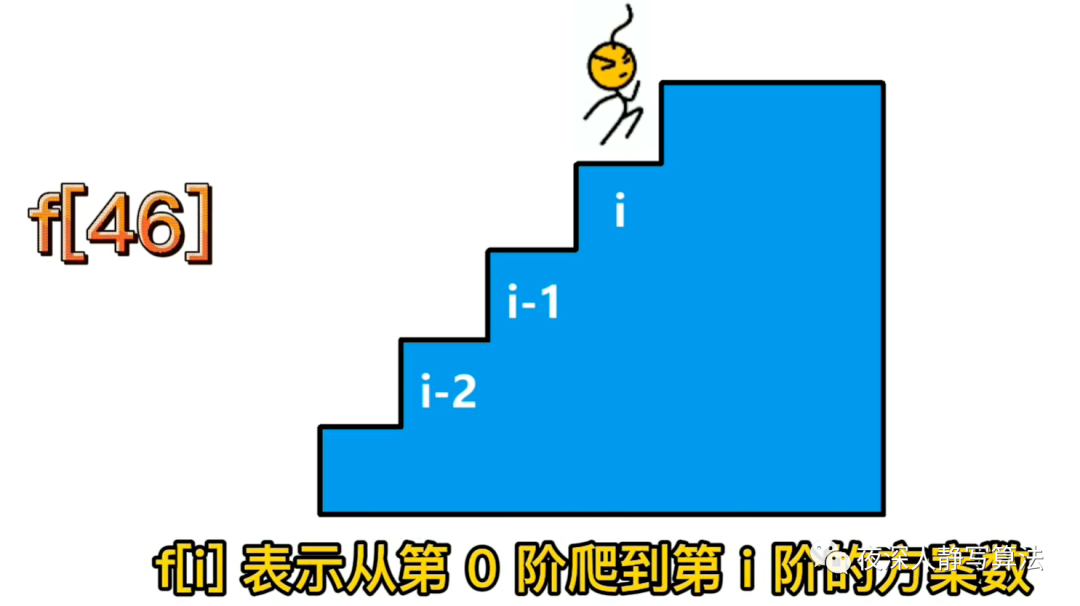
我们定义一个数组 f[46],其中 f[i] 表示从第 0 阶爬到第 i 阶的方案数。由于每次可以爬 1 或者 2 个台阶,所以对于第 i 阶楼梯来说,所以要么是从第 i-1 阶爬过来的,要么是从 i-2 阶爬过来的,如图所示:

于是得出一个递推公式:f[i] = f[i-1] + f[i-2]。
我们发现这个就是斐波那契数列,你可以叫它递推公式,也可以叫它状态转移方程。这里的 f[i] 就是状态的概念,从一个状态到另一个状态就叫状态转移。
当然我们还要考虑初始状态,f[0] 代表从第 0 阶到第 0 阶的方案数,当然就是 1 啦,f[1] 代表从第 0 阶到第 1 阶的方案数,由于只能走 1 阶,所以方案数也是 1。
代码就不再累述了。
四、二维递推问题
像斐波那契数列这种问题,是一个一维的数组来解决的,有些时候,一维解决不了的时候,我们就需要升高一个维度来看问题了。
长度为 n(1≤n<40) 的只由 ‘A’、‘C’、'M’三种字符组成的字符串(可以只有其中一种或两种字符,但绝对不能有其他字符)且禁止出现 M 相邻的情况,问这样的串有多少种?
考虑长度为 n,且以 ‘A’ 结尾的串有 f[n][0] 种、以 ‘C’ 结尾的串有 f[n][1] 种、以 ‘M’ 结尾的串有 f[n][2] 种,那么我们要求的答案就是:
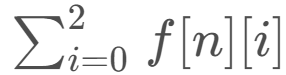
想一下怎么进行递推???
如果第 n 个结尾的字符是 ‘A’ 或者 ‘C’,那么显然, 第 n−1 个字符可以是任意字符;而如果第 n 个结尾的字符是 ‘M’,那么第 n−1 个字符只能是是 ‘A’ 或者 ‘C’。所以可以得到递推公式如下:

到这一步,我们就可以利用程序求解了,但是,还可以化解,由于
于是,可以得出:
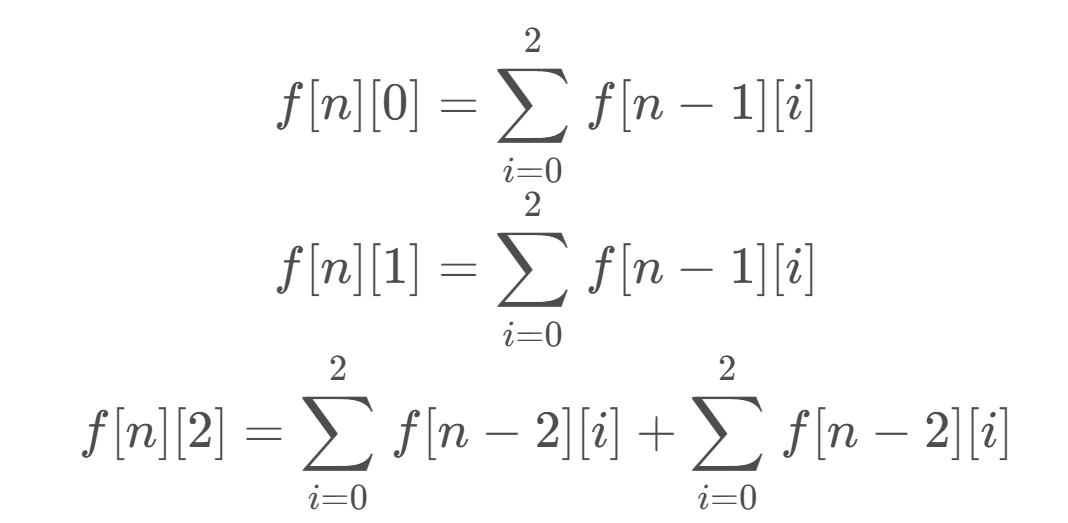
从而得到:
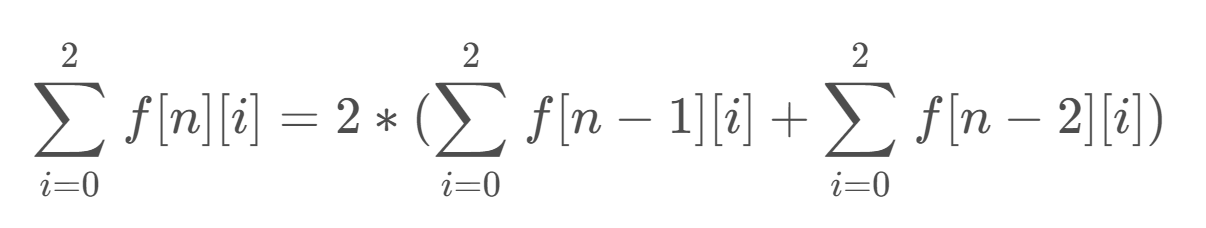
令
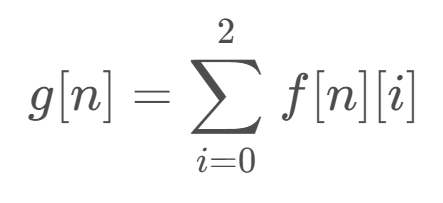
原式可以化解为如下递推式(升维再降维):
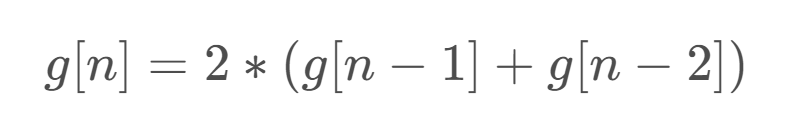
然后我们手动算出长度为 1 和 长度为 2 的串的方案数,递推代码如下:
long long getACM(int n) {
long long g[40];
g[1] = 3, g[2] = 8;
for(i = 3; i <= n; i++) {
g[i] = 2 * (g[i-1] + g[i-2]);
}
return g[n];
}