Unity版本 2022.3.13f1
Dropdown下拉菜单可以快速创建大量选项
一、 Dropwon属性详解

| 属性: | 功能: |
|---|---|
| Interactable | 此组件是否接受输入?请参阅 Interactable。 |
| Transition | 确定控件以何种方式对用户操作进行可视化响应的属性。请参阅过渡选项。 |
| Navigation | 确定控件顺序的属性。请参阅导航选项。 |
| Template | 下拉列表的模板的矩形变换。请参阅以下说明。 |
| Caption Text | 用于保存当前所选选项的文本的文本 (Text) 组件。(可选) |
| Caption Image | 用于保存当前所选选项的图像的图像 (Image) 组件。(可选) |
| Item Text | 用于保存列表项的文本的文本组件。(可选) |
| Item Image | 用于保存列表项的图像的图像组件。(可选) |
| Value | 当前所选选项的索引。0 代表第一个选项,1 代表第二个,依此类推。 |
| Options | 可能选项的列表。可为每个选项指定一个文本字符串和一个图像。 |
| On Value Changed | 用户单击了下拉列表中一个选项时调用的 UnityEvent。 |
二、创建下拉菜单
首先我们来先创建一个下拉菜单 再Unity 的Hierarchy面板右键选择UI---->Dropdown - TextMeshPro
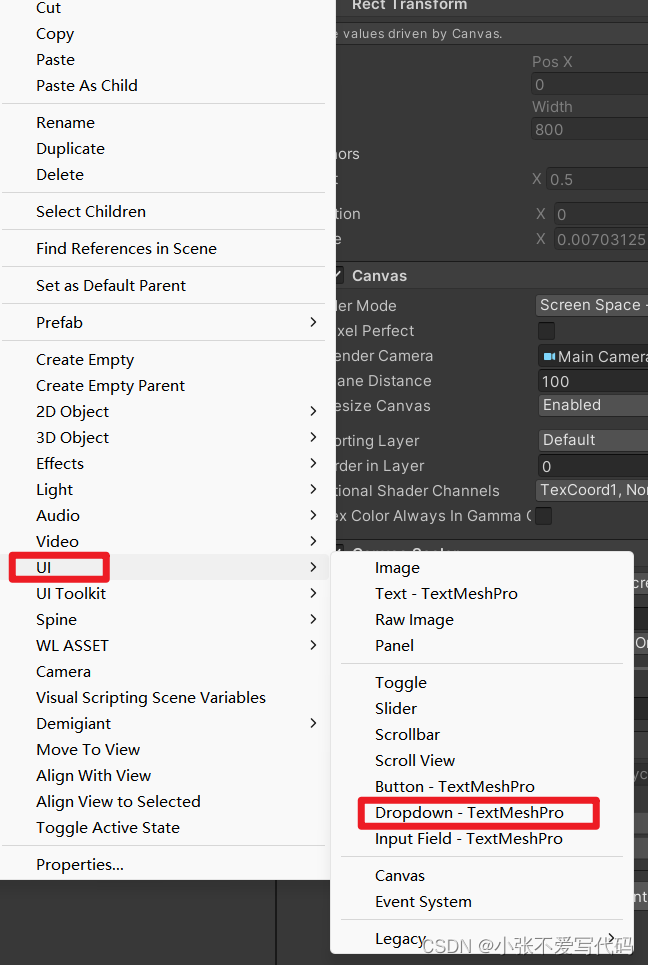
当然也可以选择Legacy里面的Dropdown 这里我们选择Dropdown-TextMeshPro
下面是Dropdown在Hierarchy面板上的层次结构

我们增加一个背景到DropDown下面作为背景展示

然后将此背景和item的背景拖拽到Dropdown组件对应的位置上面如下图所示

三、下拉菜单组件代码调用
using System.Collections;
using System.Collections.Generic;
using TMPro;
using UnityEngine;public class Test : MonoBehaviour
{public TMP_Dropdown m_Dropdown;public List<Sprite> m_Sprites;public List<string> m_TextTip;public int m_CreateTemp;private TMP_Dropdown.OptionData m_OptionData;private int lastIndex = 0;void Start(){InitDorpDown();}private void InitDorpDown(){m_Dropdown.options.Clear();for (int i = 0; i < m_CreateTemp; i++){m_OptionData = new TMP_Dropdown.OptionData();m_OptionData.text = m_TextTip[i];m_OptionData.image = m_Sprites[i];m_Dropdown.options.Add(m_OptionData);}//设置默认显示m_Dropdown.captionText.text = m_TextTip[0];m_Dropdown.captionImage.sprite = m_Sprites[0];m_Dropdown.onValueChanged.AddListener(OnChanged);}private void OnChanged(int index){if (index == lastIndex) return;lastIndex = index;Debug.Log(index);}
}
外部引用挂载
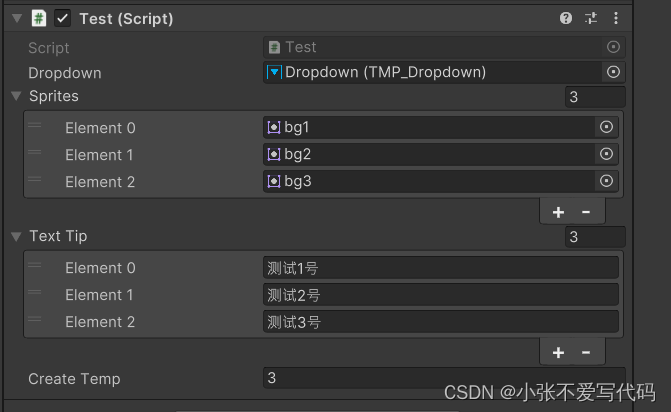
四、实际测试效果

这里是实际图片的问题上下有空白换成不留空白的图就好了
点击效果