最长异或路径

题目描述

给定一棵 $n$ 个点的带权树，结点下标从 $1$ 开始到 $n$。寻找树中找两个结点，求最长的异或路径。

异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

输入格式

第一行一个整数 $n$，表示点数。

接下来 $n-1$ 行，给出 $u,v,w$ ，分别表示树上的 $u$ 点和 $v$ 点有连边，边的权值是 $w$。

输出格式

一行，一个整数表示答案。

样例 #1

样例输入 #1

4
1 2 3
2 3 4
2 4 6

样例输出 #1

7

提示

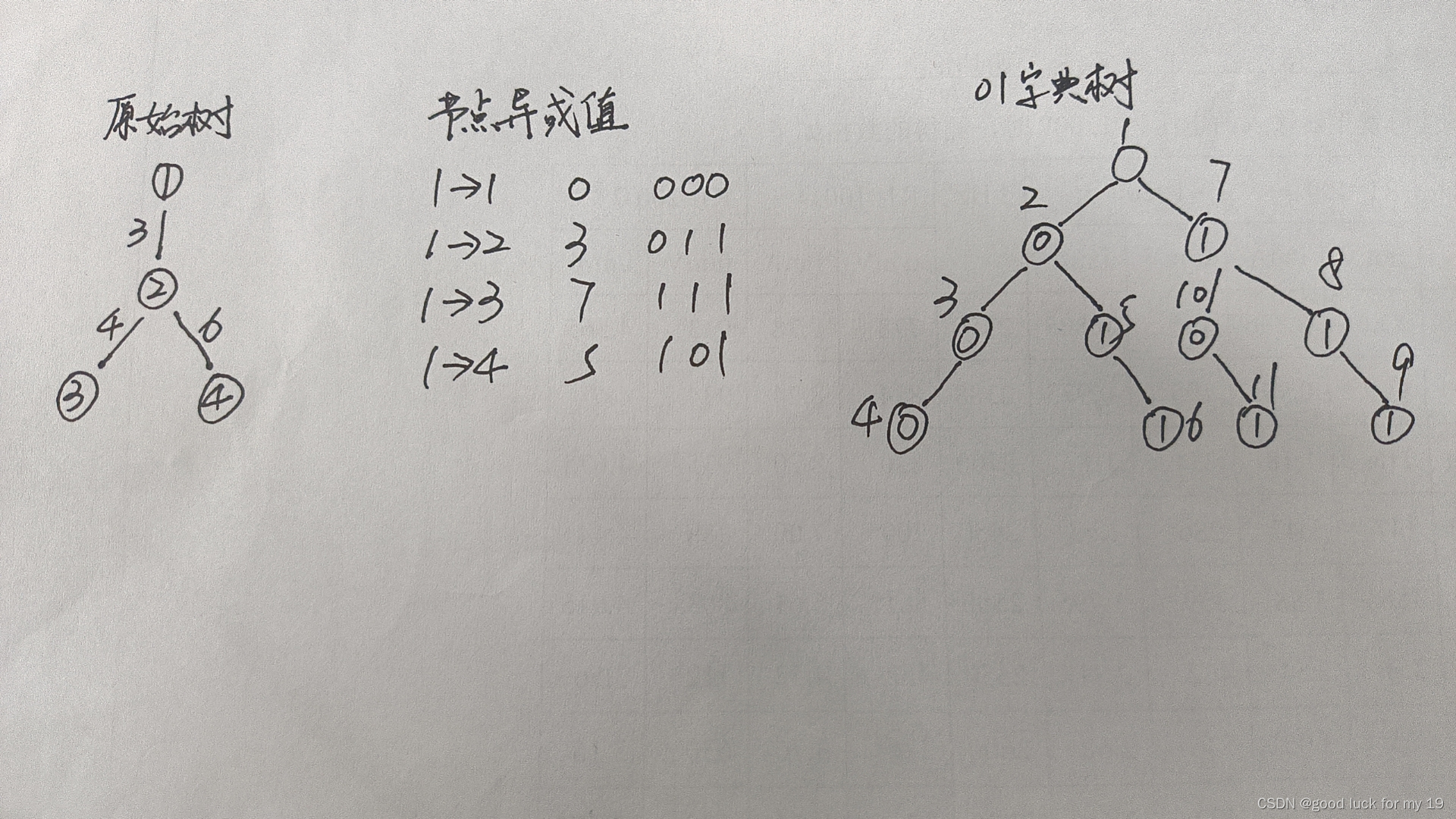
最长异或序列是 $1,2,3$，答案是 $7=3\oplus 4$。

数据范围

$1\le n\le 100000;0<u,v\le n;0\le w<2^{31}$。
插入

代码：

//每条路径 <a,b> 的 xor 和转化成 “(a 到根的 xor 和) xor (b 到根的 xor 和)”
#include<bits/stdc++.h>
using namespace std;
struct node{int left=0,right=0;
}root;
vector<node> trie;
vector<int> a[100001],b[100001];//连接情况记录在a数组，权重情况记录在b数组
int yihuo[100005];//搜索异或值的结果
//通过dfs搜出所有节点到根节点的异或值
void dfs(int x,int y){//x代表节点，y代表当前的异或值是多少for(int i=0;i<a[x].size();i++){yihuo[a[x][i]]=y^b[x][i];//当前异或值异或连接到的节点的权重dfs(a[x][i],yihuo[a[x][i]]);//继续往下搜}
}
//生成01字典树
void build(int x){//记录各个节点的左右节点编号，这里默认左节点储存0，右节点储存1int fa=0,len;//每次重新输入一个异或值生成01树的时候fa都要重新置0for(int i=(1<<30);i>0;i>>=1){//边的权值最大为2的31次方，说明边权的异或最大值也是len=trie.size();//树的节点if(x&i){//当前位为1，遍历右边的if(trie[fa].right==0){//没有右节点trie[fa].right=len;// cout<<fa<<" right "<<len<<endl;trie.push_back(root);//把空节点push_back进去fa=len;//下一次的父节点为当前的节点编号}else fa=trie[fa].right;    }else{//当前位为0,遍历左边的if(trie[fa].left==0){//没有左节点trie[fa].left=len;//给左节点编号// cout<<fa<<" left "<<len<<endl;trie.push_back(root);fa=len;}else fa=trie[fa].left;}}
}
int jisuan(int x){int ans=0,fa=0;cout<<x<<endl;for(int i=(1<<30);i>0;i>>=1){//i的初始值为1<<30是因为边的权值最大为2的31次方if(x&i){//当前位为1，由于是要求最长的异或路径，所以需要遍历左边的0，才能使得当前值为1if(trie[fa].left){ans+=i;// cout<<"left "<<ans<<" "<<trie[fa].left<<endl;fa=trie[fa].left;}else fa=trie[fa].right;}else{//当前位为0，由于是要求最长的异或路径，所以需要遍历右边的1，才能使得当前值为1if(trie[fa].right){ans+=i;// cout<<"right "<<ans<<" "<<trie[fa].right<<endl;fa=trie[fa].right;}else fa=trie[fa].left;}}// cout<<x<<" "<<ans;return ans;
}
void lesson1(){int n,x,y,z,ans=0;cin>>n;for(int i=1;i<n;i++){cin>>x>>y>>z;a[x].push_back(y);b[x].push_back(z);}dfs(1,0);trie.push_back(root);//0号节点，其左节点为0号节点，右节点为0号节点for(int i=1;i<=n;i++){build(yihuo[i]);// cin>>x;// cout<<x<<endl;// build(x);       }for(int i=1;i<=n;i++){ans=max(ans,jisuan(yihuo[i]));}cout<<ans<<endl;   // for(int i=1;i<=n;i++){//     cout<<i<<":";//     for(int j=0;j<a[i].size();j++)cout<<a[i][j]<<","<<b[i][j]<<" ";//     cout<<endl;// }// for(int i=1;i<=n;i++)cout<<yihuo[i]<<" ";//根据题目样例得到0 3 7 5// for(int i=0;i<trie.size();i++){//     cout<<i<<":"<<trie[i].left<<","<<trie[i].right<<endl;// }
}
int main(){lesson1();return 0;
}