剑指offer经典题目整理（二）-编程知识

剑指offer经典题目整理（二）

一、斐波那契数列（fib）

1.链接

斐波那契数列_牛客题霸_牛客网 (nowcoder.com)

2.描述

斐波那契数列就是数列中任意一项数字，都会等于前两项之和，满足f(n) = f(n-1) + f(n-2) 的一个数列，例如：1 1 2 3 5 8 13 21 ...

现在题目规定第一项和第二项为1，输入一个整数n，代表第n项，要求返回第n项的结果

3.思路

思路一：动态规划

斐波那契数列是动态规划中最经典简单的一个代表，其中的公式就是动态规划的状态方程，这题也是用来引入简单动态规划问题的一个经典题目

解决动态规划类的问题，需要三步：

第一步是设置状态参数n，本题中的状态参数n代表的就是斐波那契数列的第n项

第二步是根据题目意思去寻找关于n的状态方程，本题的状态方程就是f(n) = f(n-1) + f(n-2)

第三步是确定初始状态，本题中的初始状态题目给出，f(1) = 1 , f(2) = 1

确定好这三步后就可以根据状态方程和初始值去写代码了

思路二：递归与剪枝

第二种解决的思路，其实是分治思想，利用递归的方式，要想知道f(n)，就需要知道f(n-1)和f(n-2) 的结果，要知道f(n-1),就要先知道f(n-2)和f(n-3)... 不断向下递归，直到递归到初始值，就可以返回得到结果，但是这种递归会存在大量的重复计算，由于递归会形成新的栈帧，对内存和计算效率的成本都非常大，因此，通过剪枝的方式去减少重复运算，这里的剪枝，就是指，可以将递归过程中，已经计算好的结果，存入到一个容器中，避免重复运算，这里我选择用map容器去实现剪枝操作

4.参考代码

思路一：动态规划

class Solution 
{
public:int Fibonacci(int n) {if(n == 1 || n == 2){return 1;}vector<int> dp;dp.reserve(n+1);dp[0] = 0;dp[1] = 1;dp[2] = 1;for(int i = 3; i<=n;i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};

代码分析

思路二：递归与剪枝

class Solution {public:int Fibonacci_recursion(int n, map<int, int>& fib) {if (n == 1 || n == 2) {return 1;}int pre = 0;if (fib.find(n - 1) == fib.end())  //没有记录过{pre = Fibonacci_recursion(n - 1, fib);fib[n - 1] = pre;} else {pre = fib[n - 1];}int ppre = 0;if (fib.find(n - 2) == fib.end()) {ppre = Fibonacci_recursion(n - 2, fib);fib[n - 2] = ppre;} else {ppre = fib[n - 2];}return pre+ppre;}int Fibonacci(int n) {map<int, int> fib;return Fibonacci_recursion(n, fib);}
};

二、青蛙跳台阶

1.链接

跳台阶_牛客题霸_牛客网 (nowcoder.com)

2.描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

3.思路

青蛙跳台阶问题，其实就是斐波那契数列的一个变形，也是动态规划的思路去解决，同样是三步

第一步状态定义：设跳到第n台阶一共有f(n)种跳法

第二步状态方程：通过分析，可以发现，第n台阶的跳法，跳到第n阶前，要么在n-1个台阶，要么在n-2个台阶上，第n阶跳法总数会等于n-1台阶的跳法总数+n-2台阶的跳法总数，所以状态方程也就是f(n) = f(n-1) + f(n-2)

第三步初始状态：f(1) = 1,f(2) = 2

4.参考代码

class Solution {
public:int jumpFloor(int number) {vector<int> dp;dp.reserve(number+1);dp[1] = 1;dp[2] = 2;for(int i = 3;i<=number;i++){dp[i] = dp[i-1] + dp[i-2];}return dp[number];}
};

三、矩形覆盖

1.链接

矩形覆盖_牛客题霸_牛客网 (nowcoder.com)

2.描述

我们可以用 2*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形，从同一个方向看总共有多少种不同的方法？

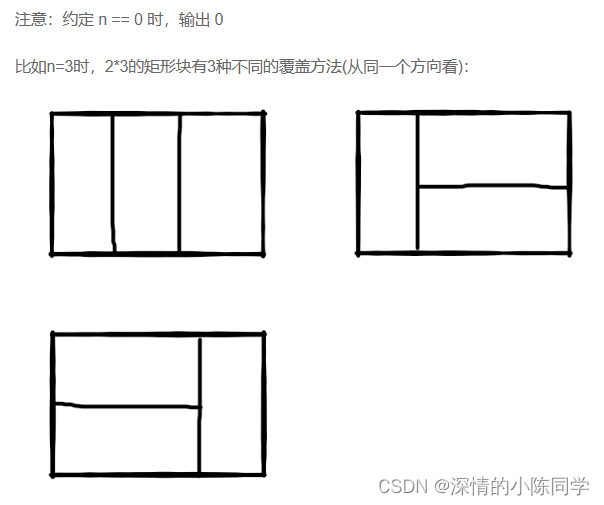
3.思路

核心还是斐波那契数列的变形，也是采用动态规划的思路

第一状态定义：用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形，从同一个方向看总共有f(n)种不同的方法

第二状态方程：每次放方块，实际只有两种放置方式，一种是竖着放（放一个），一种是横着放（放两个），类比与青蛙跳台阶一样的思路，最后放置完n个的状态，要么采用竖着放（剩下一个），要么横着放（剩下两个），而放完n个小方块的方法总数就会是这两种状态的方法总数之和

即，f(n) = f(n-1) + f(n-2)

第三初始参数：f（1）= 1 ， f(2) = 2

4.参考代码

class Solution {public:int rectCover(int number) {vector<int> dp;dp.reserve(number + 1);dp[1] = 1;dp[2] = 2;for (int i = 3; i <= number; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[number];}
};