虚拟机概念
什么是虚拟机?
虚拟机,有些时候想模拟出一个真实的电脑环境,碍于使用真机安装代价太大,因此而诞生的一款可以模拟操作系统运行的软件。
虚拟机目前有2 个比较有名的产品:vmware 出品的vmware workstation、oracle 出品的virtual Box。
虚拟机的安装
第一步:双击打开VMware安装程序
第二步:进行下一步安装
第三步:同意许可协议,单击下一步
第四步:根据需要决定是否需要更改软件的安装位置(建议放置于除C盘以外任意盘符下)
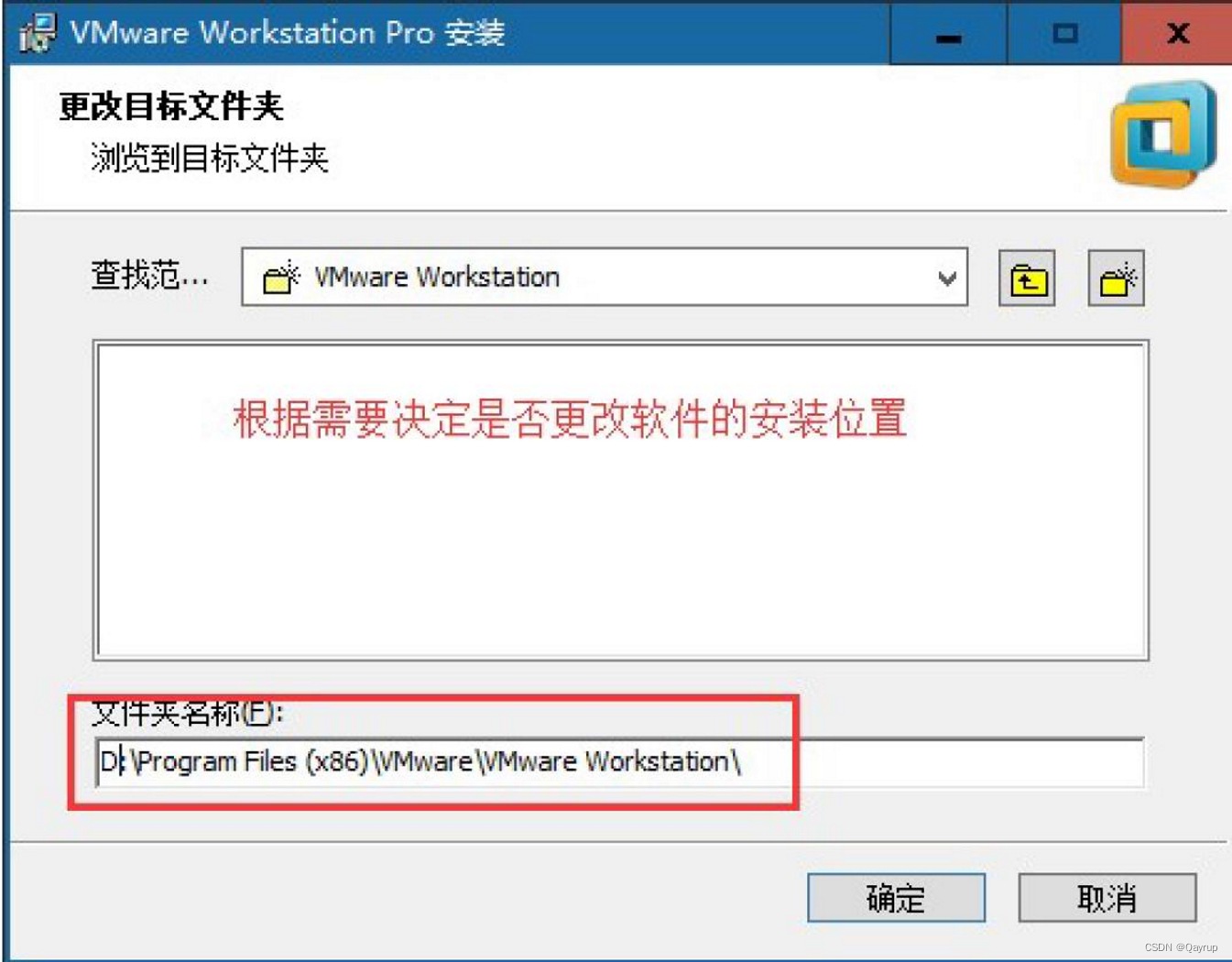
第五步:更改成功后,单击确定,下一步继续安装:
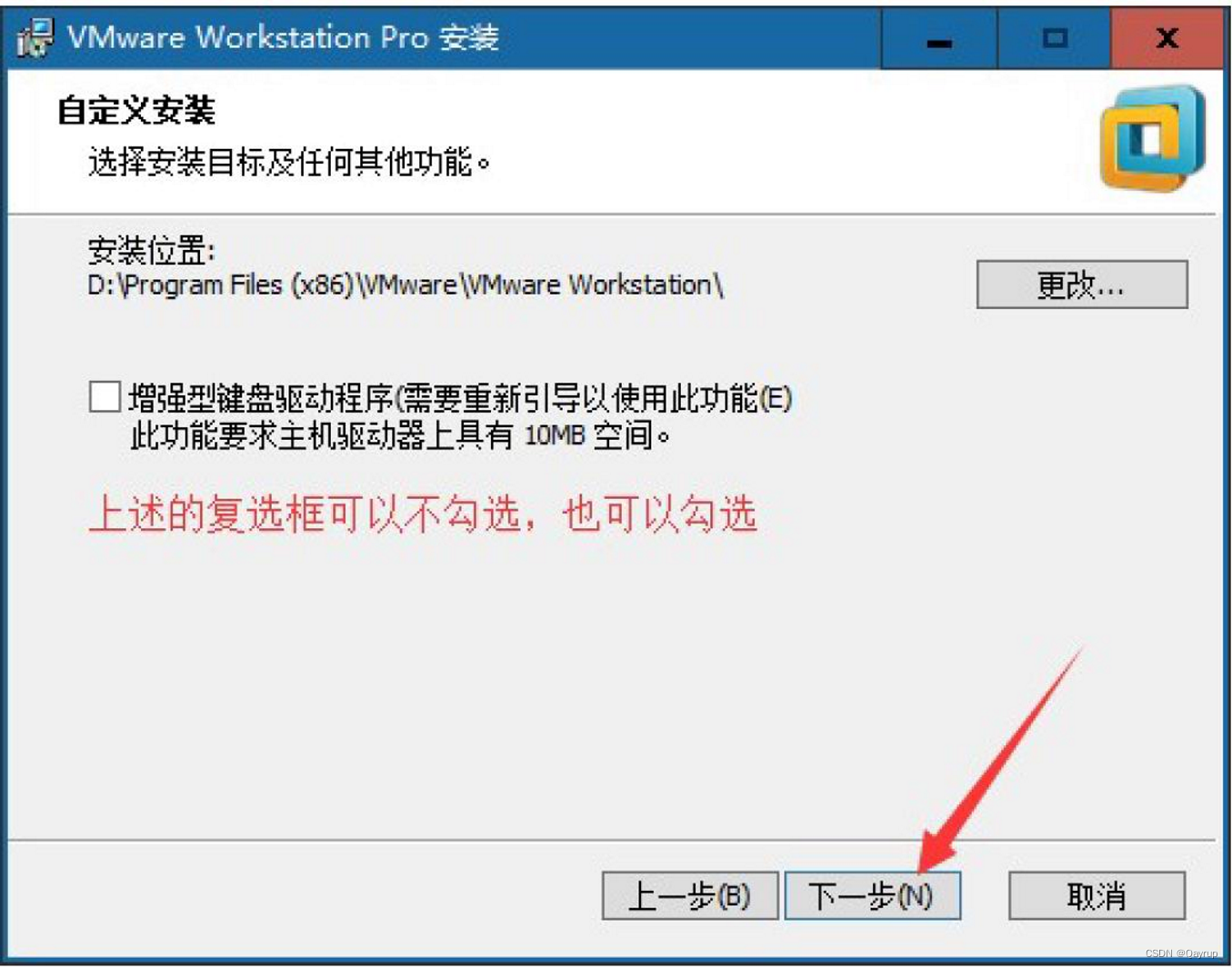
注意:所有软件的安装目录最好在安装的时候是空的
第六步:用户体验设置,如下图所示,单击下一步继续安装
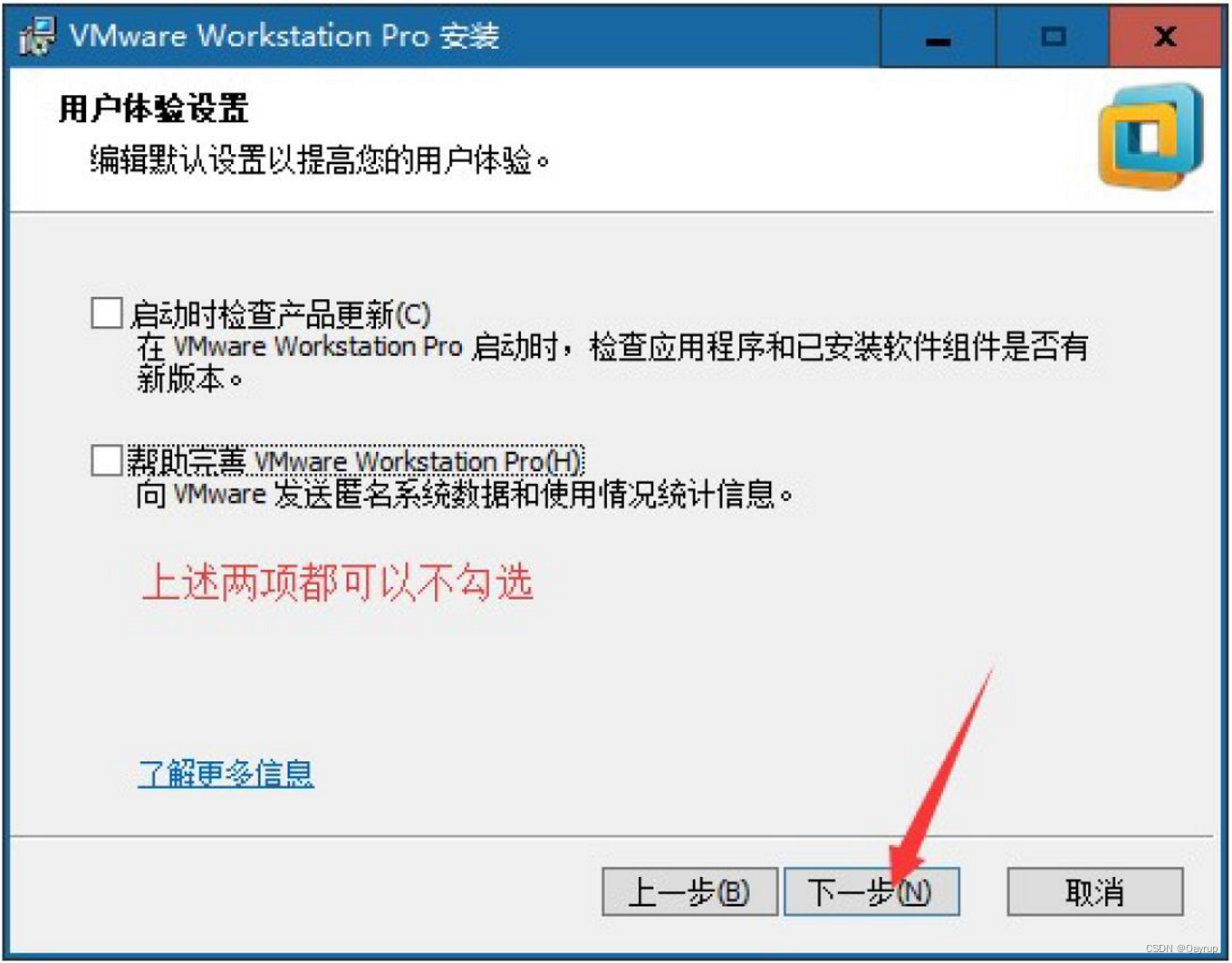
第七步:快捷方式设置,单击下一步继续安装
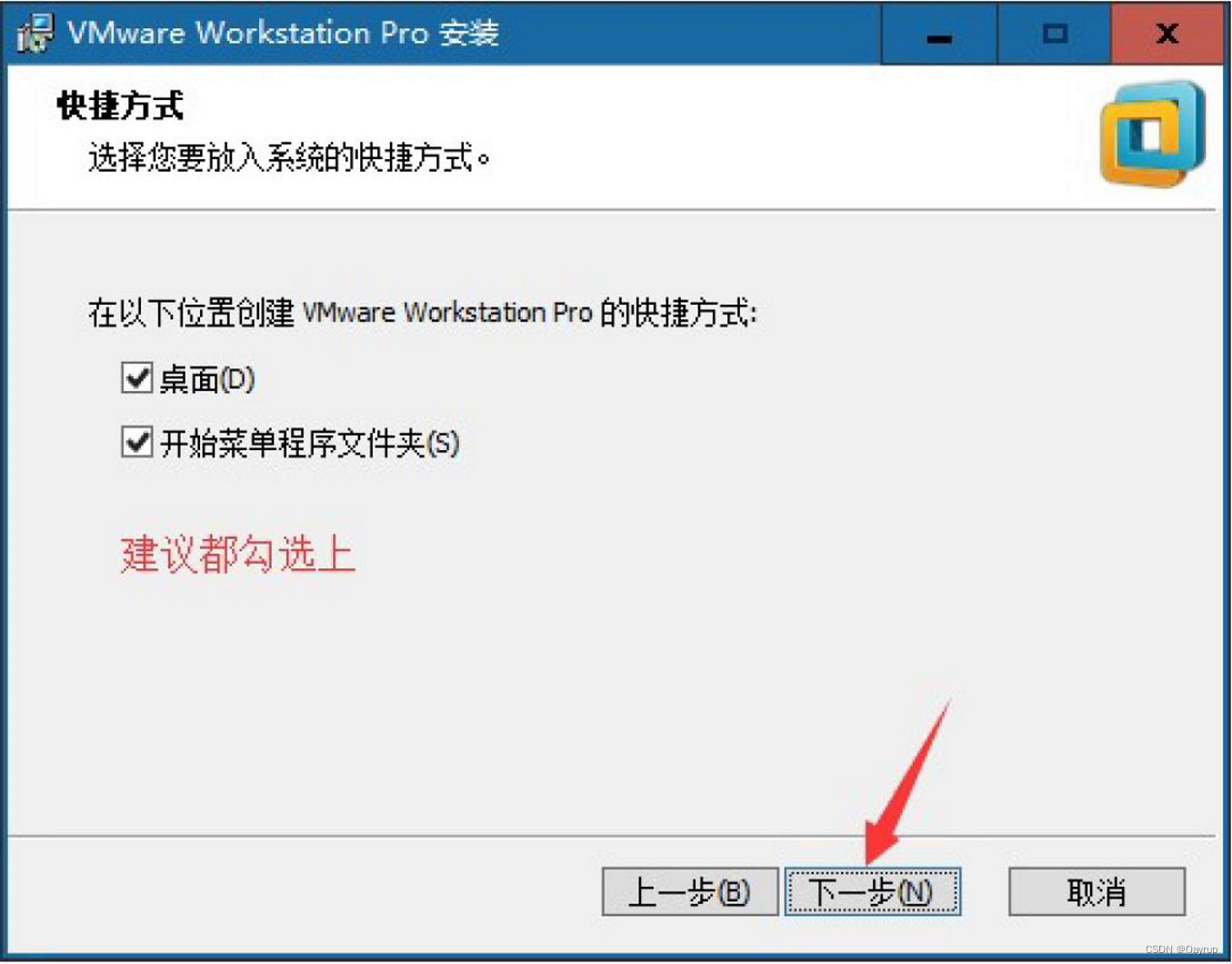
第八步:单击安装按钮
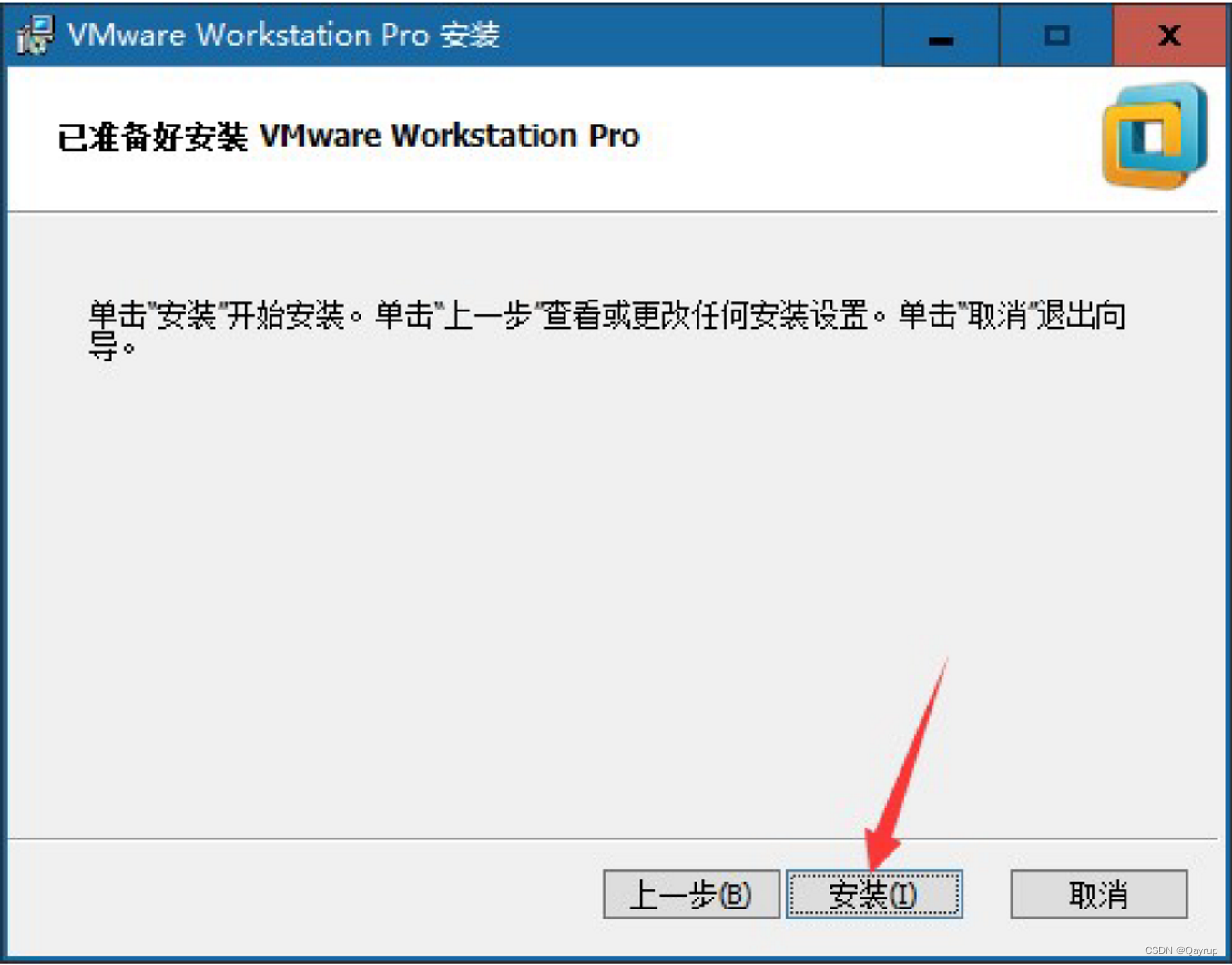
第九步:安装结束后,单击完成按钮
注意事项:最重要的地方,在安装完之后需要检查,检查虚拟机软件是否有安装2 个虚拟网卡

Windows7与Windows10可能显示网络名称有所不同,但是底部虚拟机网络是一致的。
VMware 快照与备份
VMware 快照
快照:又称还原点,就是保存在拍快照时候的系统的状态(包含了所有的内容),在后期的时候随时可以恢复。
拍摄快照
第一步:启动Linux的操作系统(快照备份是在系统启动后进行操作的)
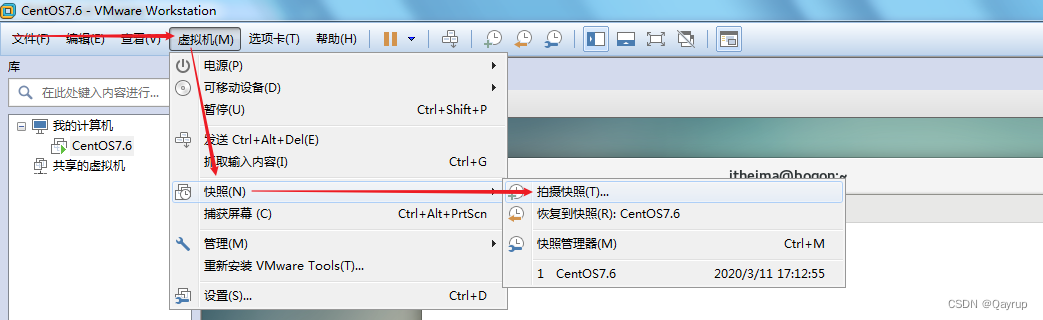
第二步:单击VMware菜单栏=>虚拟机=>快照=>选择拍摄快照
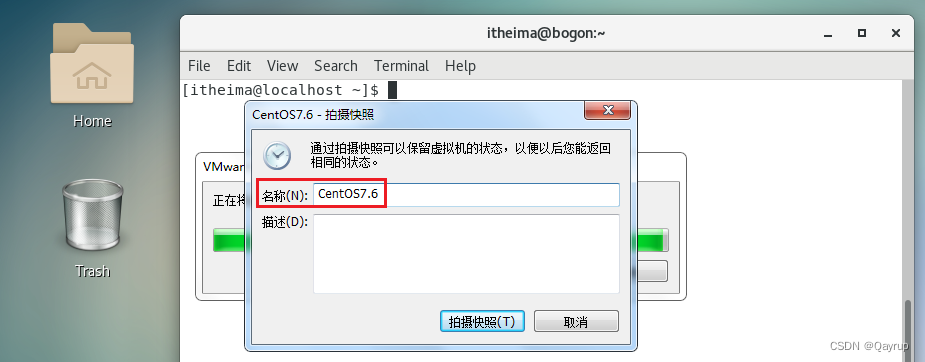
第三步:输出拍摄快照的名称(为什么要有名字?为了方便后期的恢复操作
恢复快照
第一步:模拟Linux操作系统故障(比如系统文件被删除、系统损坏等等)
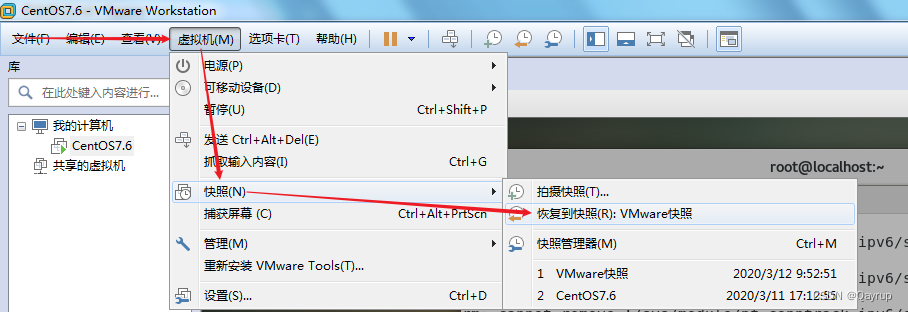
第二步:选择VMware菜单栏=>虚拟机=>快照=>恢复到快照(根据拍摄时的名称进行恢复)
快照总结
注意:侧重在于短期备份,需要频繁备份的时候都可以使用快照,做快照的时候虚拟机中操作系统一般处于开启状态
克隆
克隆:就是复制的意思。
注意事项:克隆备份不同于快照备份,其要求克隆时,操作系统必须处于关闭状态。
第一步:使用关机按钮或相关的关机命令对Linux进行关机操作
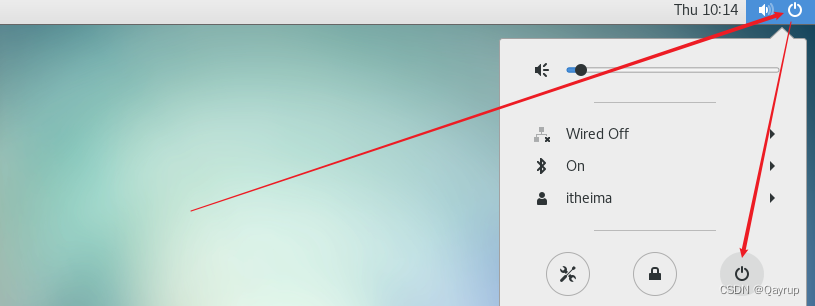
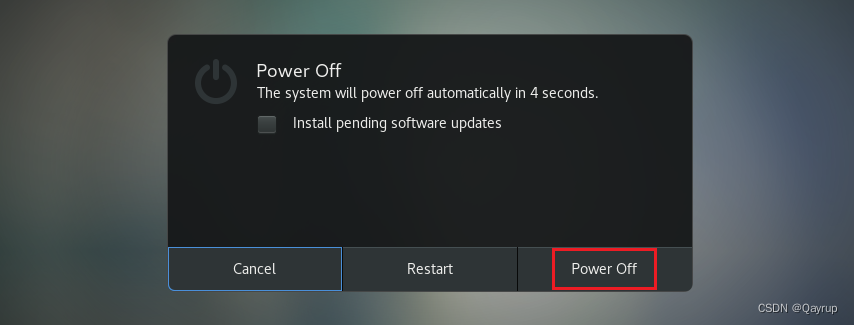
第二步:在要克隆的操作系统菜单上,鼠标右键,选择管理,选择克隆
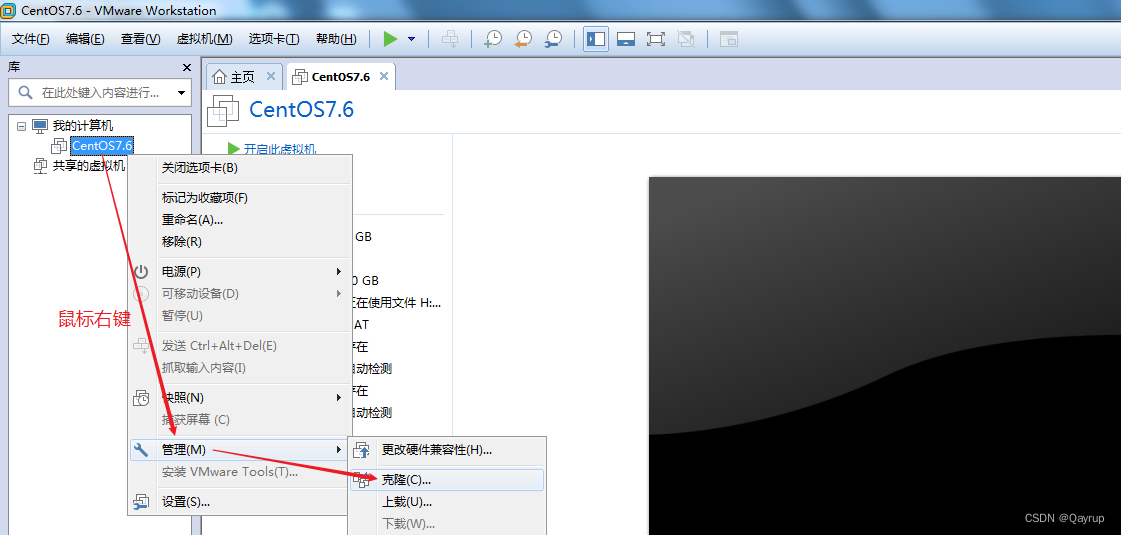
第三步:根据向导进行克隆备份
下一步、下一步,选择克隆类型,一定要选择完整克隆
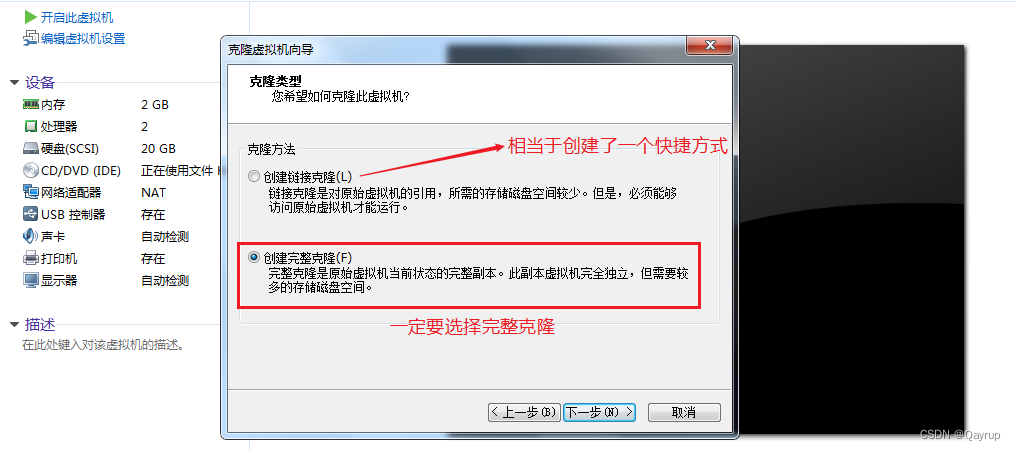
设置克隆机的名称以及存储路径(此路径剩余可用空间必须>=10G)
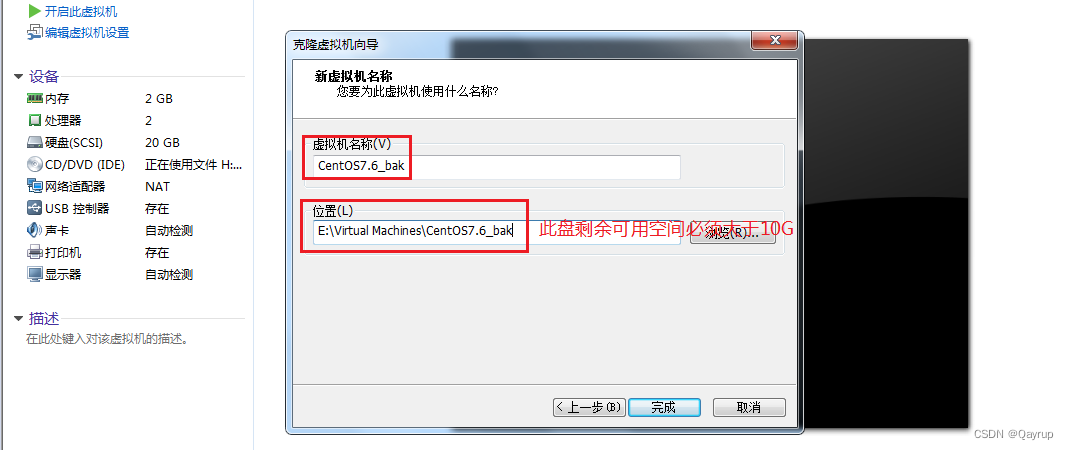
克隆完成后,效果如下图所示:产生了一个全新的操作系统
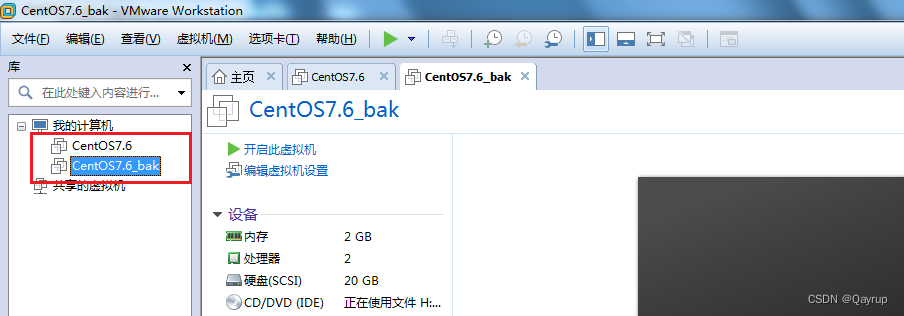
克隆总结
克隆侧重长期备份,做克隆的时候是必须得关闭操作系统(了解)
应用场景:快速创建多台计算机
快照与克隆的区别
克隆与快照的最大的区别:克隆之后是2 台机器,而快照之后依旧是1 台机器(类似windows的还原点)。后期的危险操作前建议使用快照。