💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
带电粒子在磁场和电场中移动的轨迹可以由洛伦兹力定律描述。洛伦兹力定律描述了带电粒子在电场和磁场中所受到的合力,它的表达式为:
F = q(E + v × B)
其中,F 是带电粒子所受到的合力,q 是粒子的电荷量,E 是电场强度,v 是粒子的速度,B 是磁场强度。"×" 表示叉乘。
根据洛伦兹力定律,带电粒子在电场和磁场的共同作用下,其速度和加速度会发生变化,从而导致轨迹的偏转。在三维空间中,粒子的轨迹取决于初始条件,包括粒子的初速度、初始位置以及电场和磁场的性质。
在一个恒定的磁场中,带电粒子将遵循螺旋状轨道,被称为洛伦兹轨道。这是因为磁场对粒子施加一个垂直于速度方向的力,使得粒子不断弯曲向心,形成一个螺旋形轨道。
在存在电场的情况下,电场会对带电粒子产生力,使粒子加速或减速。因此,带电粒子的轨迹将不再是简单的螺旋形状,而是受到电场力的影响而产生偏移。
需要注意的是,粒子的质量、电荷、速度、磁场和电场的特性等因素都会影响轨迹的形状和特征。因此,具体的轨迹方程需要通过数值模拟或解析方法来求解,具体取决于系统的参数和初始条件。
总结起来,带电粒子在磁场和电场中移动时的轨迹是一个复杂的问题,取决于粒子的初始条件以及磁场和电场的性质。通过洛伦兹力定律,可以描述其受到的合力,但具体的轨迹方程需要根据具体情况进一步分析和计算。
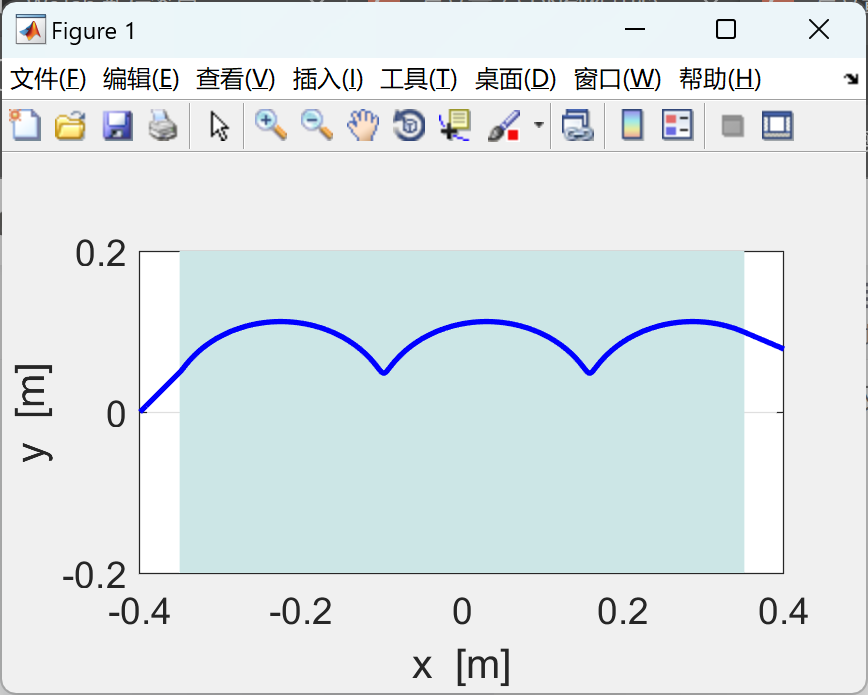
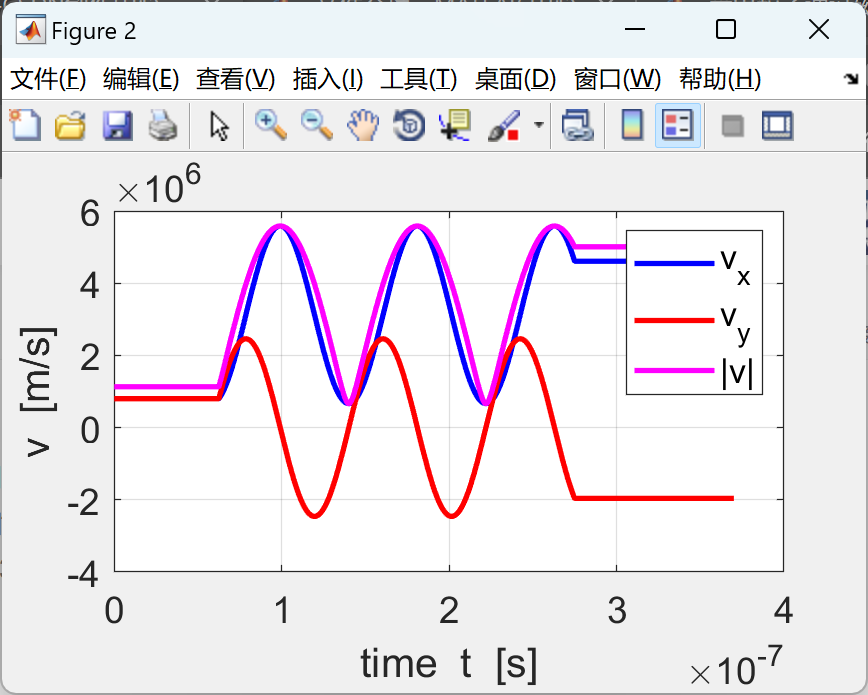
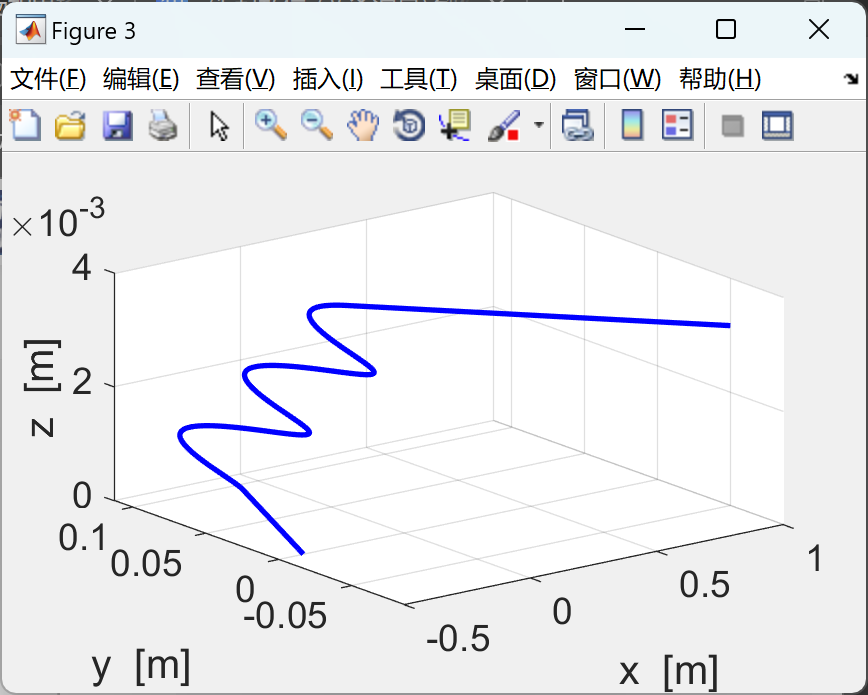
使用有限差分法求解由洛仑兹力定律推导出的带电粒子在均匀磁场或均匀电场或交叉磁场和电场中的运动方程。mscript 的图形输出汇总了仿真中使用的参数、
XY 平面中的轨迹以及 3D 轨迹和位移、速度和加速度时间图。
📚2 运行结果
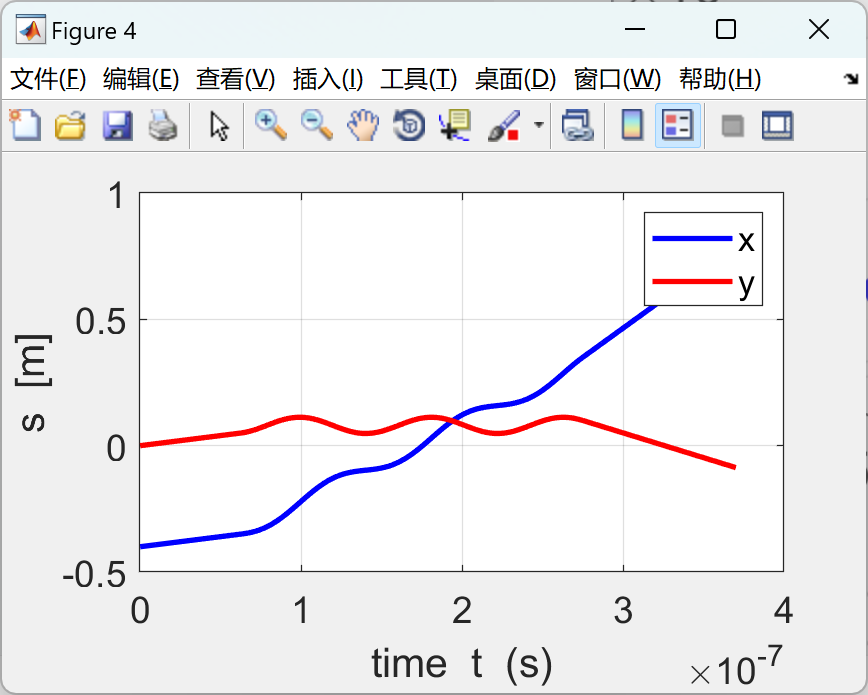
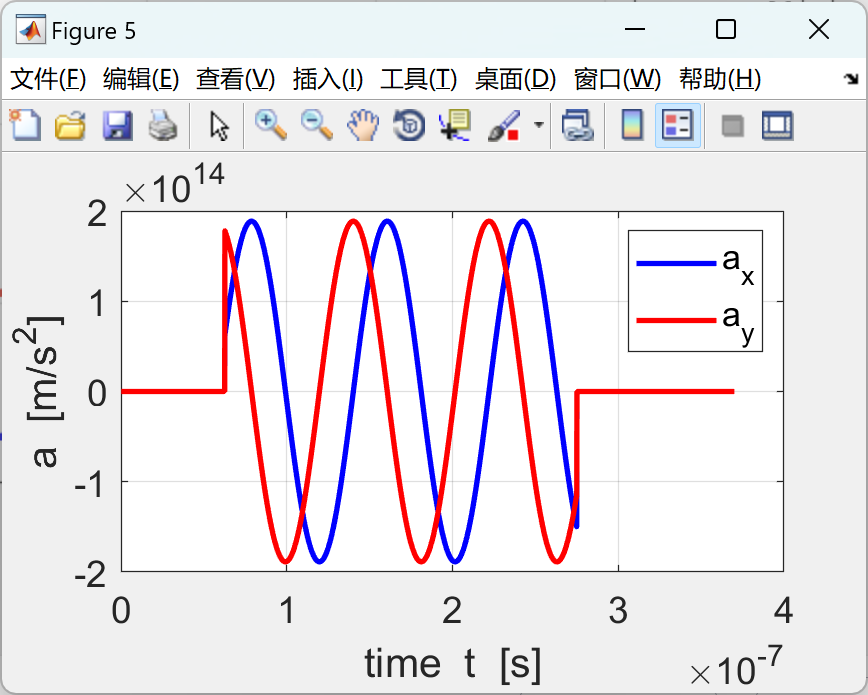
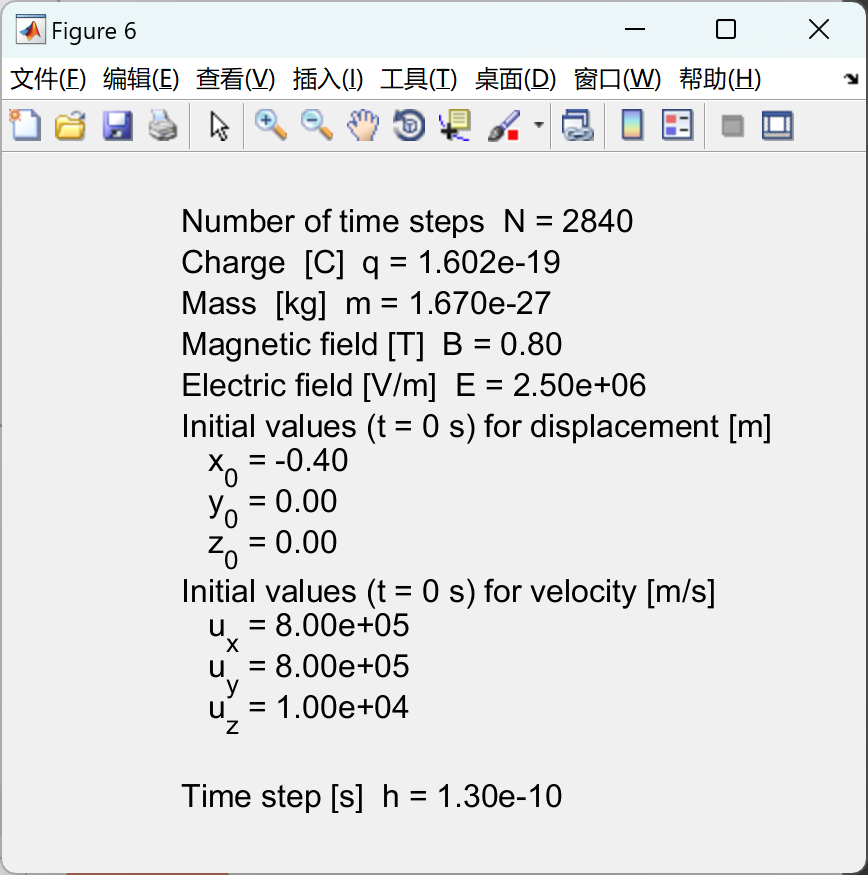
部分代码:
figure (5) % -------------------------------------------------------------
set(gcf,'units','normalized','position',[0.36,0.1,0.3,0.3]);
xP = t; yP = ax;
plot(xP,yP,'b','LineWidth',2)
hold on
xP = t; yP = ay;
plot(xP,yP,'r','LineWidth',2)
xlabel('time t [s]');
ylabel('a [m/s^2]');
legend('a_x','a_y');
grid on
set(gca,'fontsize',14);
figure (6) % -------------------------------------------------------------
set(gcf,'units','normalized','position',[0.67,0.1,0.3,0.4]);
xP = 0; yP = 0;
plot(xP,yP,'b','LineWidth',2)
axis([0 100 0 100]);
fs = 12;
px1 = 10; py1 = 98; dpx = 5; dpy = 7; px2 = 50;
% Number of elements N
tx1 = 'Number of time steps N = ';
tx2 = num2str(N,'%4.0f\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
% charge q
py1 = py1 - dpy;
tx1 = 'Charge [C] q = ';
tx2 = num2str(q,'%2.3e\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
% charge m
py1 = py1 - dpy;
tx1 = 'Mass [kg] m = ';
tx2 = num2str(m,'%2.3e\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
% magnetic field B
py1 = py1 - dpy;
tx1 = 'Magnetic field [T] B = ';
tx2 = num2str(B,'%2.2f\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
% electric field E
py1 = py1 - dpy;
tx1 = 'Electric field [V/m] E = ';
tx2 = num2str(E,'%2.2e\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
axis off
% initial positions x y z
py1 = py1 - 1*dpy;
tx1 = 'Initial values (t = 0 s) for displacement [m]';
tx2 = ' ';
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
py1 = py1 - 1*dpy;
tx1 = ' x_0 = ';
tx2 = num2str(x(1),'%2.2f\n');
tx3 = ' ';
tx = [tx1 tx2 tx3];
h_text = text(px1,py1,tx); set(h_text,'fontsize',fs);
py1 = py1 - dpy;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
1. Griffiths, D. J. (2017). Introduction to Electrodynamics (4th ed.). Cambridge University Press.
- 书籍中的第11章介绍了带电粒子在电场和磁场中运动的基本理论和轨迹。
2. Reitz, J.R., Milford, F.J., & Christy, R.W. (2013). Foundations of Electromagnetic Theory (4th ed.). Addison-Wesley.
- 本书第9章探讨了带电粒子在电场和磁场中运动的数学描述和轨迹分析。
3. Purcell, E.M., & Morin, D.J. (2013). Electricity and Magnetism (3rd ed.). Cambridge University Press.
- 该教材的第5章涵盖了带电粒子在电场和磁场中的运动以及相关的轨迹描述。