目录
前言
引入:
基本概念和术语
数据
数据元素
数据项
数据对象
数据结构
逻辑结构
物理结构
数据类型
为什么要设计出来数据类型呢?
数据类型的分类
抽象数据类型
数据结构与算法的关系
算法
定义
特性
设计要求
效率度量方法
事后统计方法
事前统计方法
示例:
函数的渐进增长
时间复杂度
定义:
常数阶
线性阶
对数阶
平方阶
效率比较
最坏情况与平均情况
空间复杂度
总结
前言
本片文章主要介绍数据结构的引入的诸论知识,也很重要属于整个数据结构的基础,希望对大家有所帮助(●'◡'●)
引入:
早期人们以为计算机是计算的,把它当作一个数值运算工具,而计算机解决问题的方式是——先从具体问题中抽象出一个合适的数据模型,设计一个解决这个数据模型的算法,接着编写程序,然后得出结构
而数据结构是一门研究非数值计算的程序问题中的操作对象,以及它们之间的关系和操作等相关问题的学科。
而要想进一步了解数据结构到底是什么,就要先谈谈它相关基本知识的一些概念。
👇
基本概念和术语
数据
数据是指描述客观事物的符号,可以在计算机中操作的对象
数据分为非数值类型和数值类型,数值类型就是像平常中的小数阿、整数等,有具体数值的数,而非数值类型是包含字符和声音、图像、视频等
例如,MP3音频就是指数据——声音数据
而任何一个符号都可以成为数据吗?
当然不是,符号要满足一定的条件才可以成为数据
- 可以输入到计算机中
- 可以被计算机程序处理
数据元素
是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理,也被称为记录
数据往下分类可以分为数据元素,这里举个例子吧——人类这个数据中的数据元素就是人
数据项
数据对象再往下分就是数据项了,它是数据不可分割的最小单位。
例如人再次细分——可以分为它的姓名阿、年龄、学校等数据项
虽然它是最小单位但是对于研究一个数据——通常研究的是数据元素。
数据对象
数据对象是相同性质的数据对象的集合,是数据的子集。
这个相同性质指得是——数据元素有相同类型和数量的数据项。
数据结构
这时候终于绕回主题了,数据结构顾名思义讲的就是数据元素之间的关系,而数据结构从两种角度分析可以分为两种——
- 1.逻辑结构
- 2.物理结构(存储结构)
逻辑结构
这里的逻辑结构讲的是数据之间的逻辑关系——这里的逻辑关系(结构)分为四种
集合结构
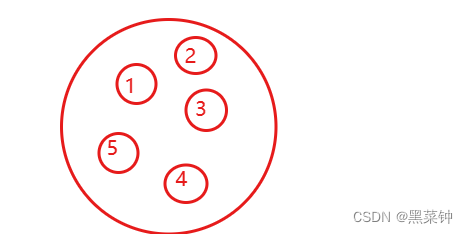
线性结构
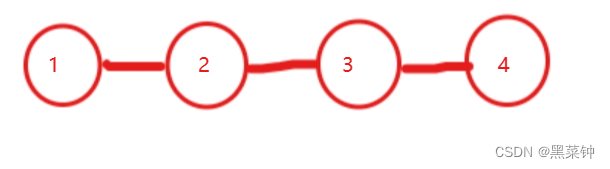
树形结构
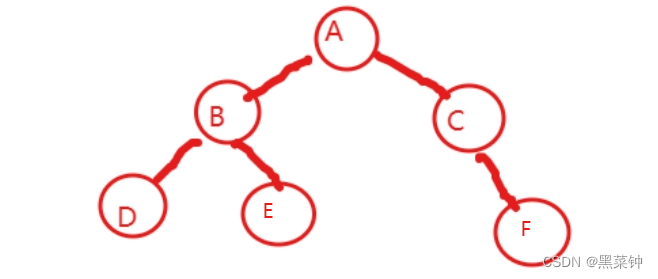
图形结构
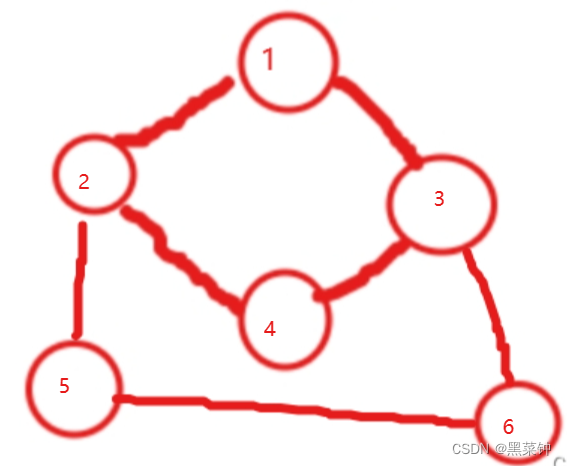
物理结构
物理结构又称为存储结构——指得是数据的逻辑结构在存储器中存储的方式,这里的存储器主要是指内存,而硬盘、U盘等为外部存储器
这里也分为两类结果
- 顺序存储结构
- 链式存储结构
顺序存储结构是指——像数组一样,排列在一起,把数据存放在一个连续的区域内,就像排队一样,一个人挨着另一个人
链式存储结构——就是不把数据存放到一块地方,而是放在不同的地方,但是这样就无法体现逻辑结构了,因此这个链式存储的每一个数据的存储空间要加上一个指针,指向下一个位置
数据类型
数据类型想必大家已经很熟悉了吧,它的概念是——性质相同的值的集合及定义在此集合的一些操作的总称
那为什么要设计出来数据类型呢?
因为在计算中对于不同类型的值,它们的内存占用不同,计算方式也有所差异,因此,计算机的研究者考虑,对数据进行分类,然后分出多种数据类型
数据类型的分类
分为原子类型和结构类型
是不可分解的基本类型——整型、实型、字符型等
有若干个类型组合而成,可以再分解,例如结构体和数组,对于数组而言它是由若港人相同类型数据组成的
抽象数据类型
对于高级语言程序员来说,所有的问题,我们只需要编写一个程序就可以,不需要考虑它在计算机里是如何转化的,如何运行的,因此对于很多问题而言,我们可以只把问题的本质抽象出来解决即可。那么这里就引出了一个概念——抽象数据类型(ADT)
一个数据模型及定义在该模型上的一组操作
其中的抽象是指把问题的本质给保留,而非本质的东西舍去,意义在于数据类型的数学操作特性
抽象数据类型包含一个数据对象,数据对象中各数据元素之间的关系,在数据元素上进行的一系列操作
ADT 抽象数据类型名
Data 数据元素之间楼及关系的定义
Operator操作1初始条件操作结果描述操作2……
endADT抽象数据类型体现了问题分解、抽象、信息隐藏的特性
数据结构与算法的关系
我们经常可以看到所谓的数据结构和算法放到一起讲,但是算法和数据结构明明是两个概念?
为什么经常把他们放到一起呢?
——因为他们密不可分
数据结构与算法的关系就像——电影里的罗密欧与朱丽叶,当电影只讲其中的一个人的时候这个电影或许就没这么好看了,但是它们一旦结合到一起去讲,这个电影就完整了。
类比到数据结构——专讲数据结构那么结果会导致你不知道它到底创造出来是干嘛用的,但是当结合算法后你就会明白创造出这个概念的人真是很厉害。
数据结构是一个问题的抽象出来的形式,而算法是通过这个数据结构来解决这个问题。
但是一般来说大学中算法和数据结构往往分开讲解,算法是为了更好的理解数据结构
算法
定义
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或者多个操作
特性
可行性
就是算法的每一步都是可行的
有穷性
算法在执行有限的步骤后自动结束,而不是陷入死循环
确定性
算法的每一条都必须有确定的含义,不能有二义性
输入输出
算法有0或者多个输入,但是必须至少有1个输出——因为如果一个算法不输出的话,这个算法干嘛用的?
设计要求
正确性
代码设计肯定现要求正确阿
可读性
这个代码不光是你自己看,要让其他的看你代码的人可以理解,这就是可读性
健壮性
如果输入了一些奇怪的数据,算法也要有相应的措施
时间效率高且存储量低
算法设计要时间的效率高,假如一个算法需要运行几天,那不是要命,而且要求存储量低,也就是数据占有的空间少,最好的是花最少的时间,用最少的存储空间
效率度量方法
既然在算法的设计要求里有效率高这一要求,(这里的效率是指算法的运行时间)那么效率该怎么去衡量呢?
事后统计方法
通过设计好的测试程序和数据,利用计算机的计时器对不同算法编制的程序运行时间比较,从而确定算法效率的高低。
在刚开始,是利用事后统计方法计算的效率,而这种方式就是让程序先运行一遍,然后在使用计算机中的计时器去计算这个程序所运行的时间,来由此估量效率
而这种方法会存在几个坏处
1.算法的测试数据困难——对于一些程序而言,它们可能更适合大量的数据,这时候输入的少量数据,反而会导致判断整个的效率低,而我们无法把每一种测试可能都测试一遍,所以设计测试数据比较困难
2.必须先依据算法事先编写好程序,但是这个往往需要大量时间,假如这个算法很烂,那么完全是在浪费时间
3.时间的比较往往依赖于计算机的硬件和软件等因素。
事前统计方法
因此针对于事后统计的坏处,一些人设计了一种在程序运行之前就可以计算它效率的方案——事前统计方法,利用统计方法来计算代码的运行次数,来因此判断其效率的大小
一个用高级程序语言编写的程序在计算机运行所消耗的时间主要取决于

⭐最终在分析程序的运行时间时,最重要的是把程序看成独立于程序设计语言的算法或者一系列步骤
示例:
这个算法是计算从0——100的和,这一种算法执行了2n+4次
int sum=0;//执行1次 int n=100;//执行1次 for(int i=0;i<n;i++)//执行n+1次 {sum=sum+i;//执行n次 } printf("%d",sum);//执行1次
这个程序运行了n*n+2次
int sum=0,n=100,x=0;//执行1次 for(int i=1;i<=n;i++) {for(int j=1;j<=n;j++){x++;sum=sum+x;//执行n*n次} } printf("%d",sum);//执行1次
函数的渐进增长
对于函数f(n)和g(n)来说,总是存在n>N,使得f(n)<g(N),这样就说明g(n)的增长渐进大于f(n)
那么根据这个定义我们可以引出两个规则——在这个算法效率度量时,可以把加法常数给忽略,把最高此项的系数常数给忽略。
因为它们在n的不断增加,它们的作用几乎没有,其实本质上算出来的算法效率——只看最高次项的指数。它越大那么函数随着n的增长也会增长很快。
这也就是事前统计方法的理论依据
时间复杂度
时间复杂度就是指算法的时间效率的估算。
定义:
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级,算法的时间复杂度,也就是算法的时间度量,记作:T(n)=O(f(n))。表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度,f(n)为问题规模n的某个函数
时间复杂度的计算方法通常称为——大O记法
一般来说,T(n)随着n增长增长速度最慢的算法为最优算法
这个方法的步骤如下:
- 把所有的加法常数变为1
- 把除最高次项以外的项舍去
- 如果最高次项有系数,那么除于这个系数
- 得出结果
下面介绍几个常见的时间复杂度
常数阶
O(1)
从大O记法来说,所有的常数阶,不论这个常数为多少,都记作O(1)
也就是说程序运行时间与问题的大小——即n的大小无关,称为常数阶
例如:
int i=1,sum=0;sum=sum+i;sum=sum+i;这段代码就是一个典型的常数阶
线性阶
O(n)
线性阶的循环结构会比较复杂,通过确定莫格特定的语句或者语句段运行的次数来计算某个算法的阶数🔚
也就是说时间复杂度为O(n)的程序,因为其循环体中的代码要执行n次。
很典型的例子就是for循环——
for (int i=0;i<n;i++)
{//一行语句,时间复杂度为O(1)
}对数阶
O(log n)
对数阶主要存在于用while循环的结构
在一个while循环中:
int count =1;
while(count<n)
{count=count*2;
}每次count乘以2,count就离n靠近一点,也就是说当2^m>n时循环结束,m指count乘以2的次数,也是这行代码运行的次数——m=log2n
记为O(logn)
平方阶
O(n^2)
对于循环嵌套循环的情况下,循环中的语句可能运行次数为n的平方次,记为O(n^2)
典型的案例如下:
for (int i=0;i<n;i++)
{for (int j=0;i<n;i++)
{//一行语句,时间复杂度为O(1)
}
}效率比较
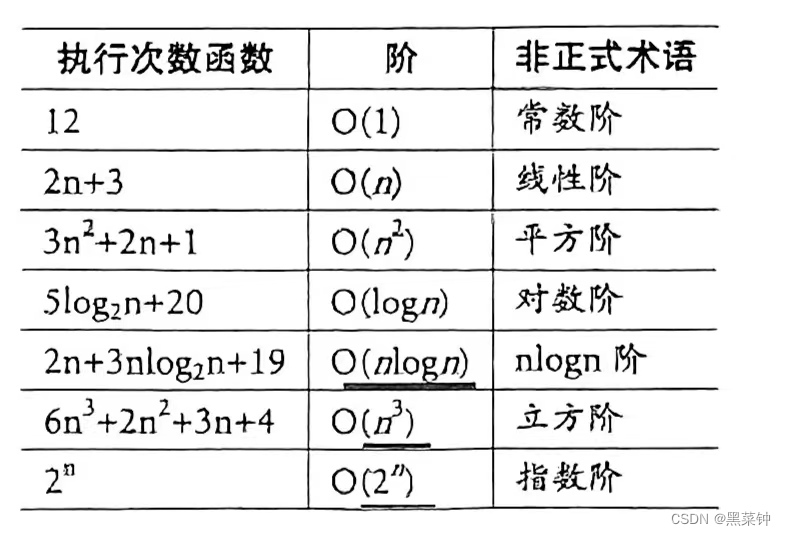
最坏情况与平均情况
最坏情况运行时间是一种保证,它是最慢的一种情况,考虑这个最坏的情况,那么对于一般的情况不会比这更慢了。
通常我们提到的运行时间都是指最坏情况的运行时间
平均时间情况是期望中的运行时间,所有情况的平均值,也是所有情况中最有意义的。
空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作S(n)=O(f(n)),n为问题的规模,f(n)为语句关于n所占的存储空间的函数
空间复杂度的概念是——这个程序在内存中所占用的大小
通常复杂度如果不注明的话——一般是指时间复杂度
总结
🆗到这里这个数据结构的知识就介绍完毕了,下面就开始一些具体的数据结构了——线性表、栈等,欢迎订阅合集,点赞收藏哦✌