模型分析与偏差和方差-编程知识

在创建一个机器学习系统，当我们的模型出现问题时，我们需要去找到最优的方式，能解决我们的问题，这时我们就需要会去诊断问题。

模型评估(Evaluating a model)：

1.训练集和测试集判断：

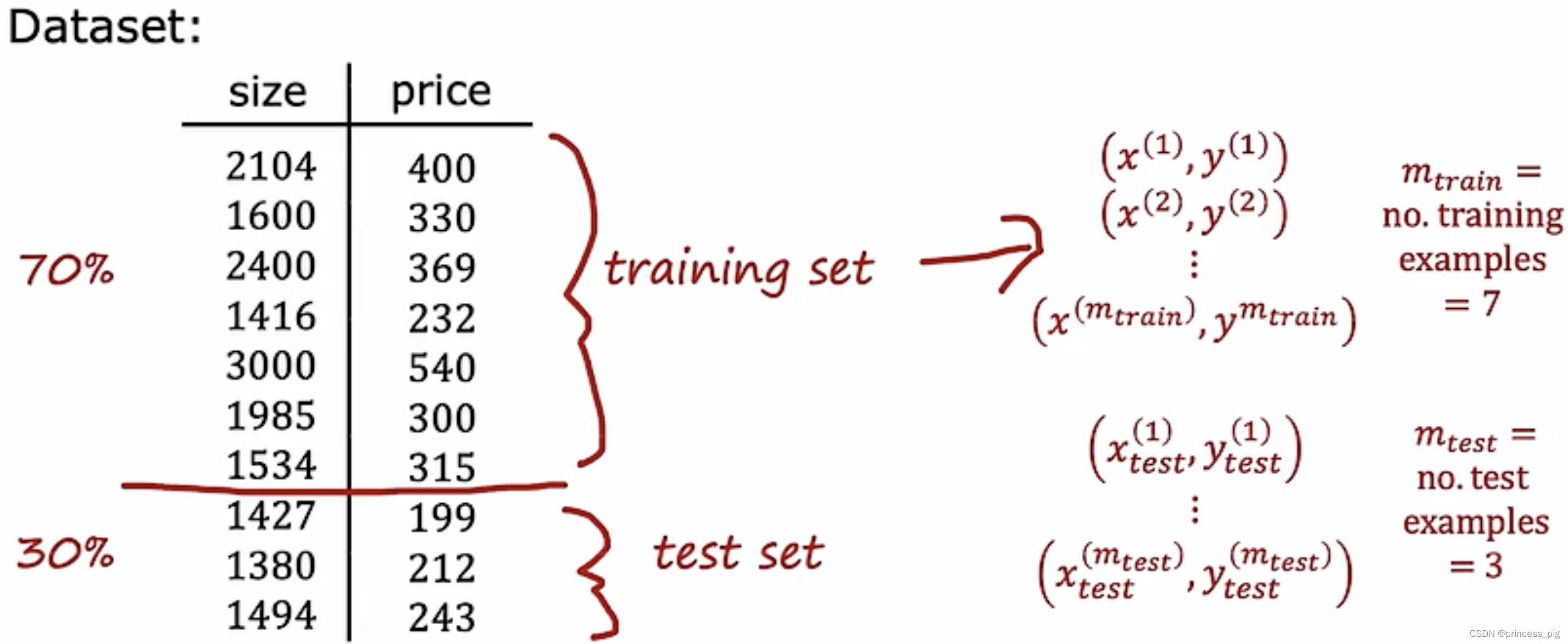
我们一般把数据组的前70%，使用为我们的训练集，而我们的数据组的最后30%，一般被我们认为是测试集。

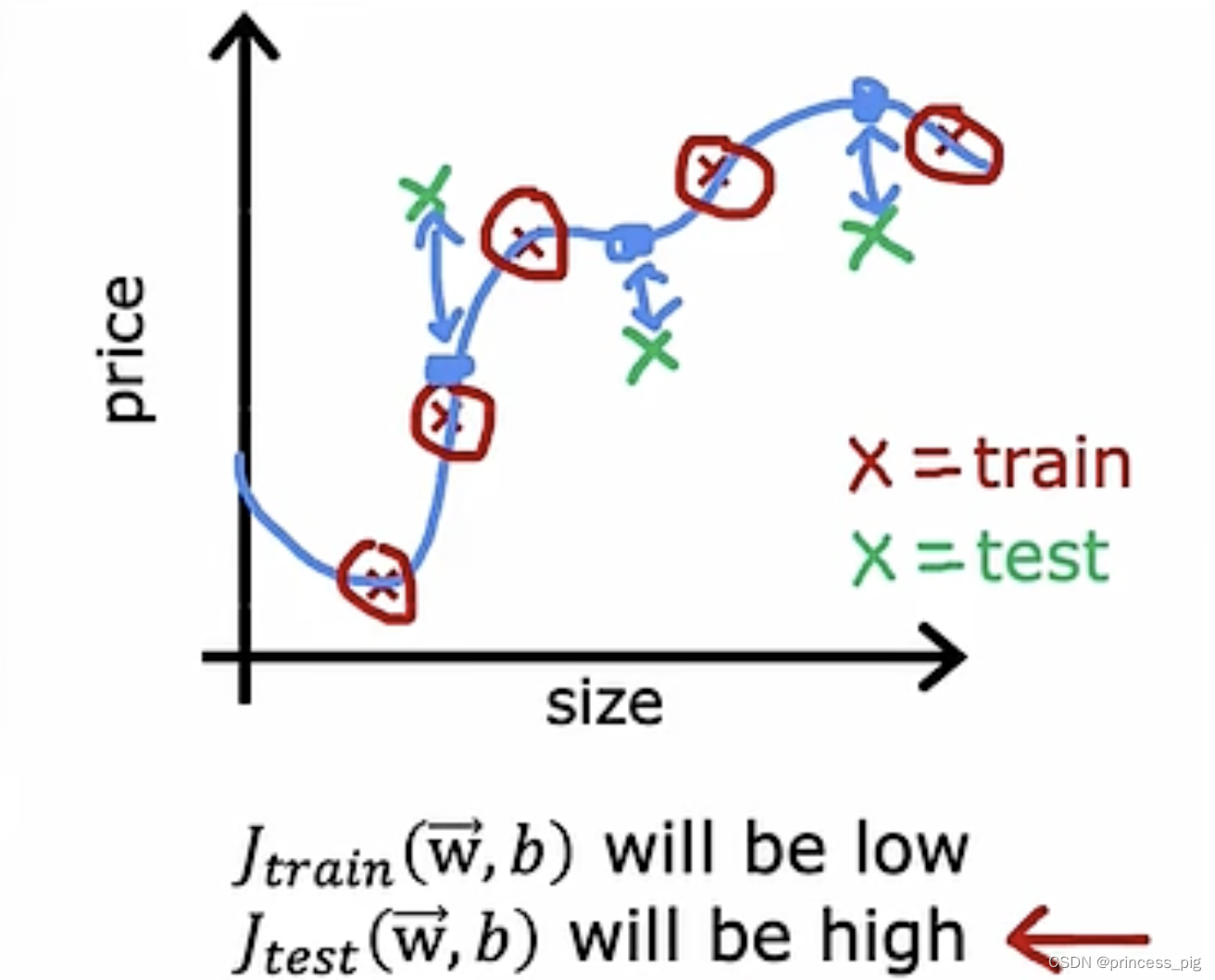
我们可以看到得到的一个根据训练集画出的函数模型，对于训练集来说，误差会非常小，甚至等于0，而我们的测试集，则是我们并没有把我们的数据输入，所以它的误差会非常的大。这里用的是成本函数。

这时一个很好的方法，可以让我们判断我们的算法是否合适。

2.训练交叉验证测试集：

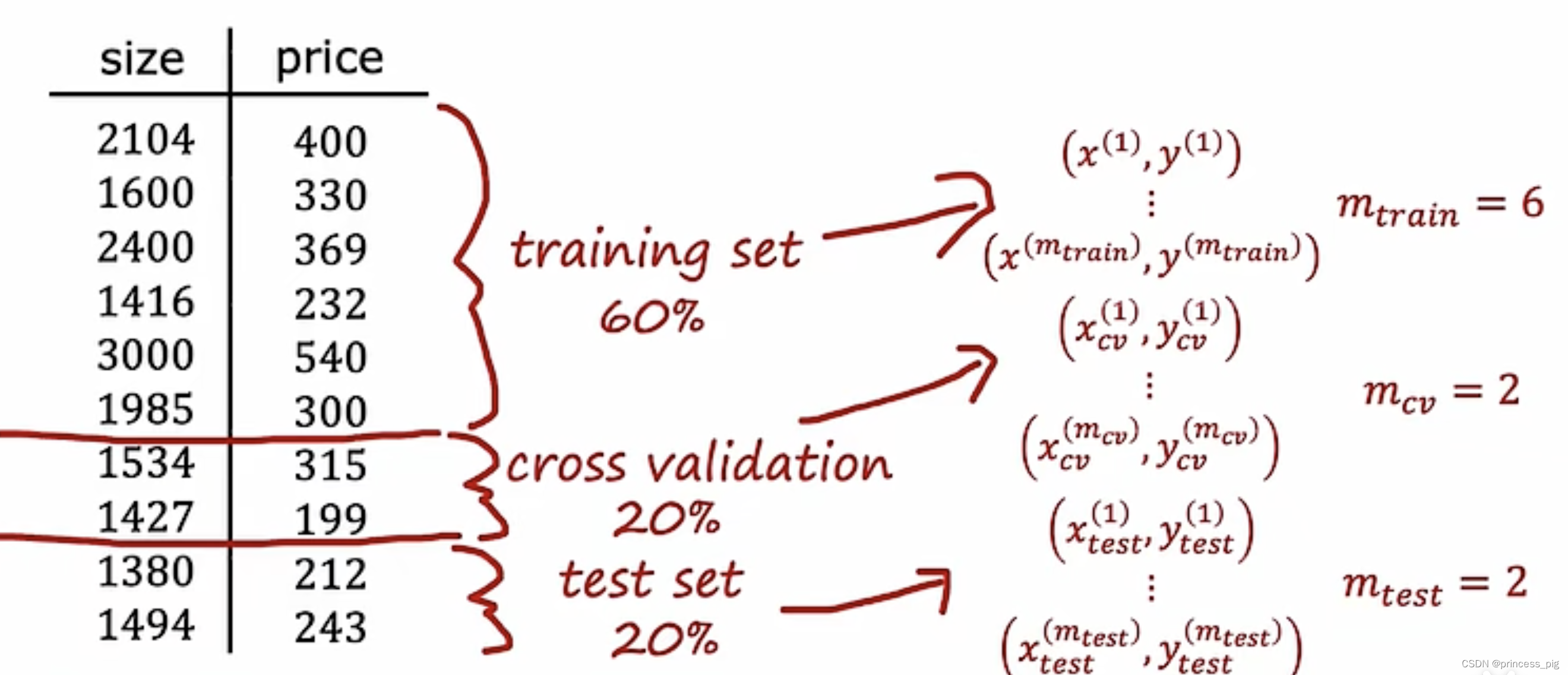
我们把我们的数据分为三个部分，训练集，交叉验证集(dev set)，测试集三个部分。

在我们的交叉验证集，去先测试我们的训练集训练得到的模型，这时我们的测试集也是我们之前没有使用的数据，我们更具交叉验证集验证得到的模型也会在测试集中测试也会非常的合适。

偏差与方差：

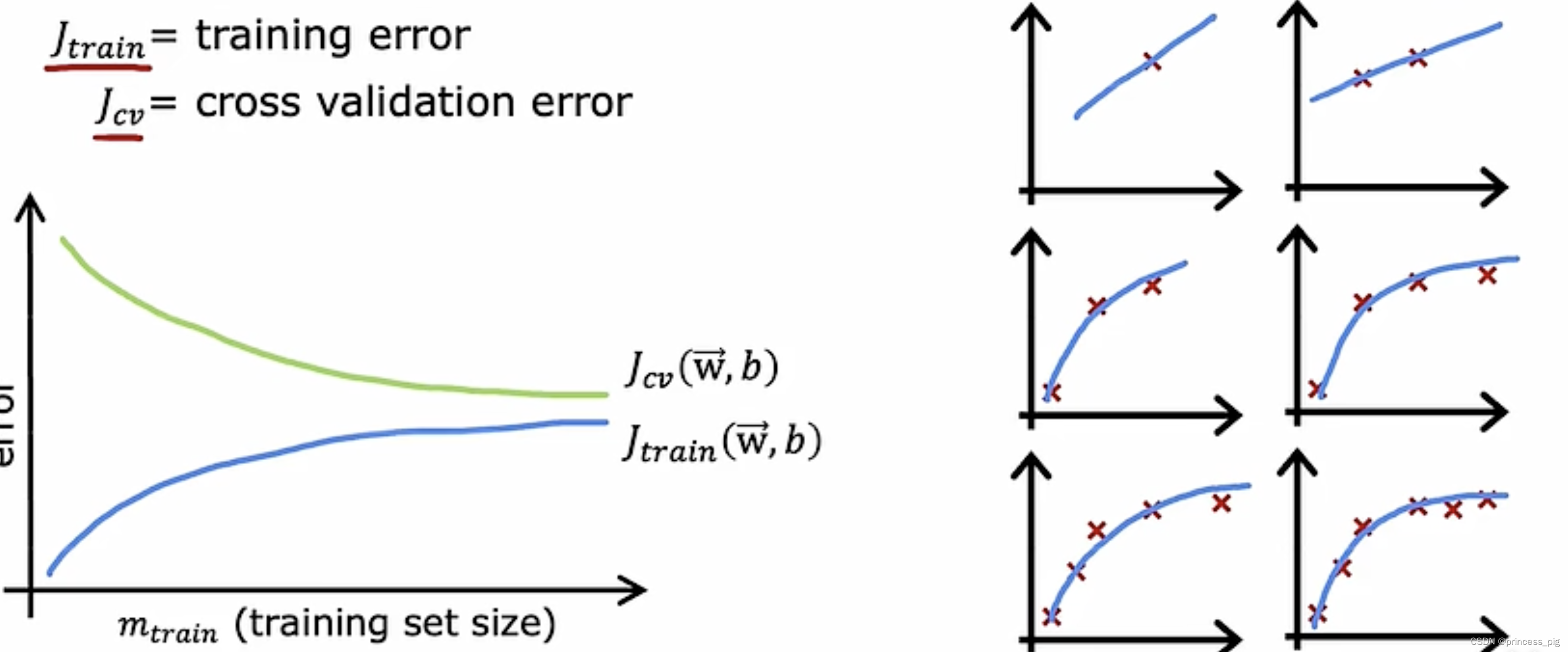
以上这个图给我们介绍了三种情况，在次数不同时，对与训练集和我们的交叉验证集不同的偏差，很明显只有我们的d=2时，才可以完全的适应这个预测的函数，无论是Jtrain还是Jcv.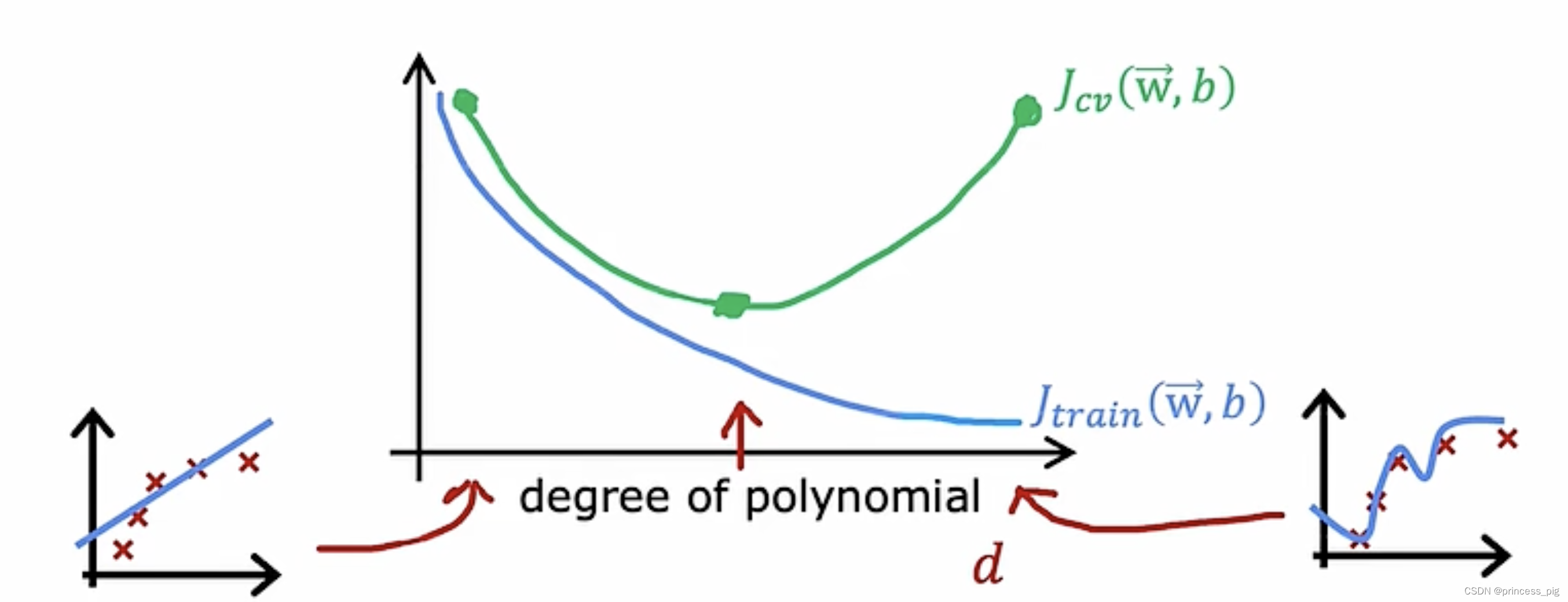

所以我们在上图中可以发现，当我们的多项式的次数增加时，我们的训练成本函数会不断的下降，而我们的交叉验证成本函数并不是这样的一个趋势，它会在我们从最小的次数到最大的次数中的一个次数，达到它的最小值。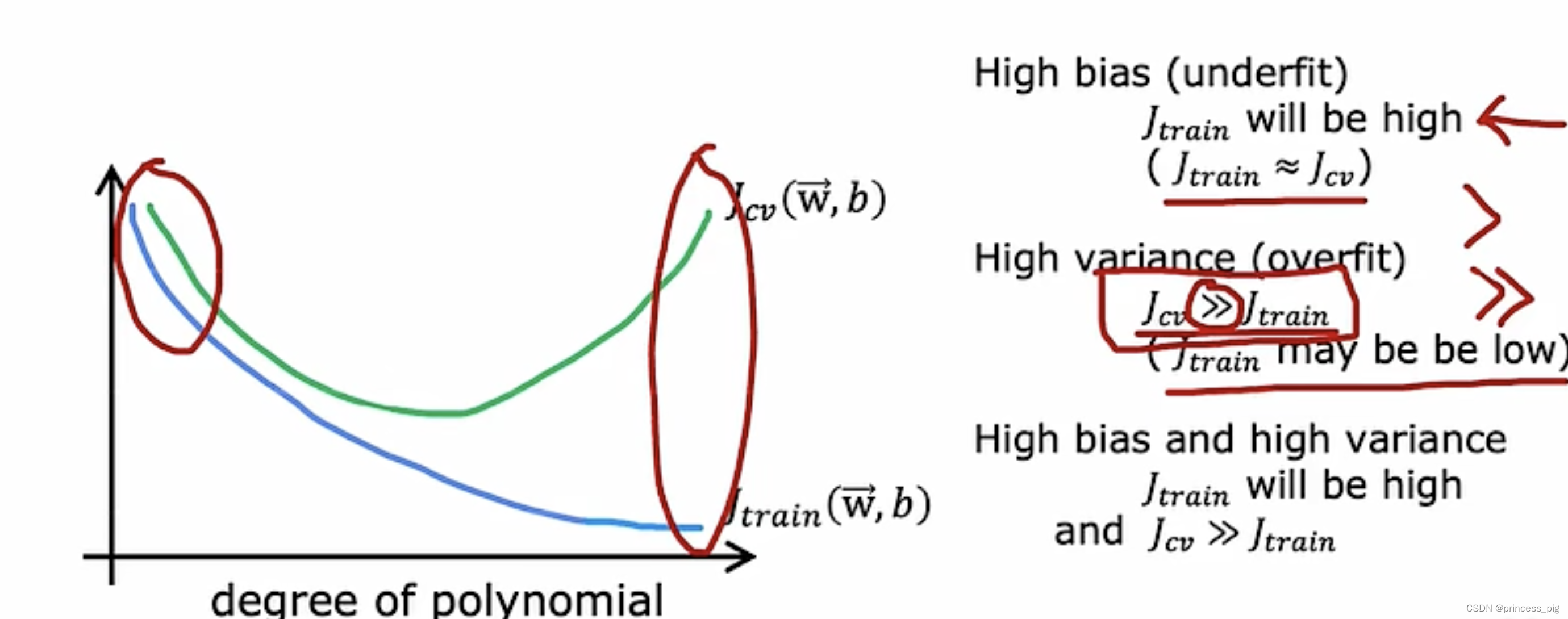

这是我们的算法需要注意的一个点，通过它我们可以知道是，偏差过大，还是方差过大。

正则化：

我们对于 $\lambda$ 的取值，影响着我们对于拟合函数的影响，上图介绍了我们两个比较极端的情况，很大与很小。

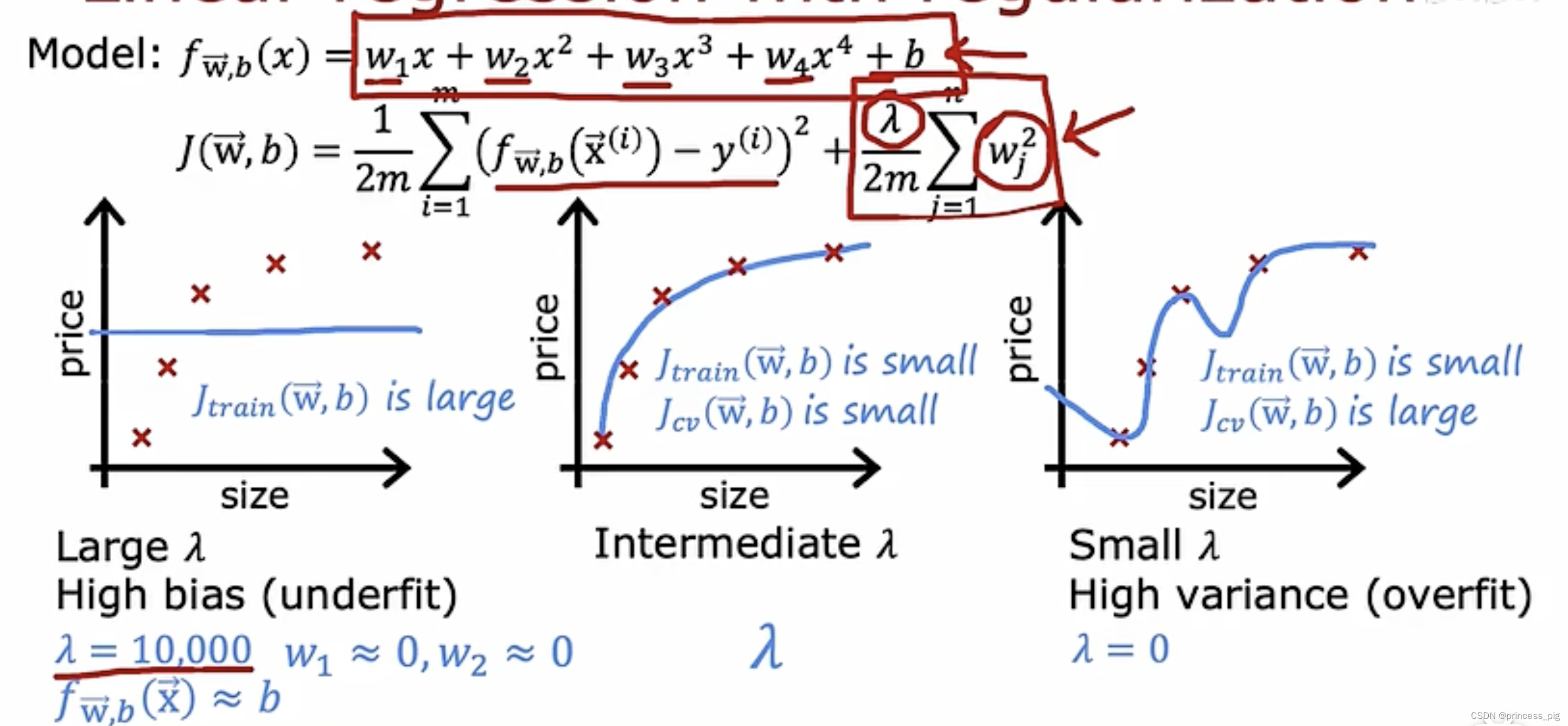
这样我们就可以去根据尝试不同的 $\lambda$ 的值，去得到我们最合适的权重，使得我们的Jcv最小。

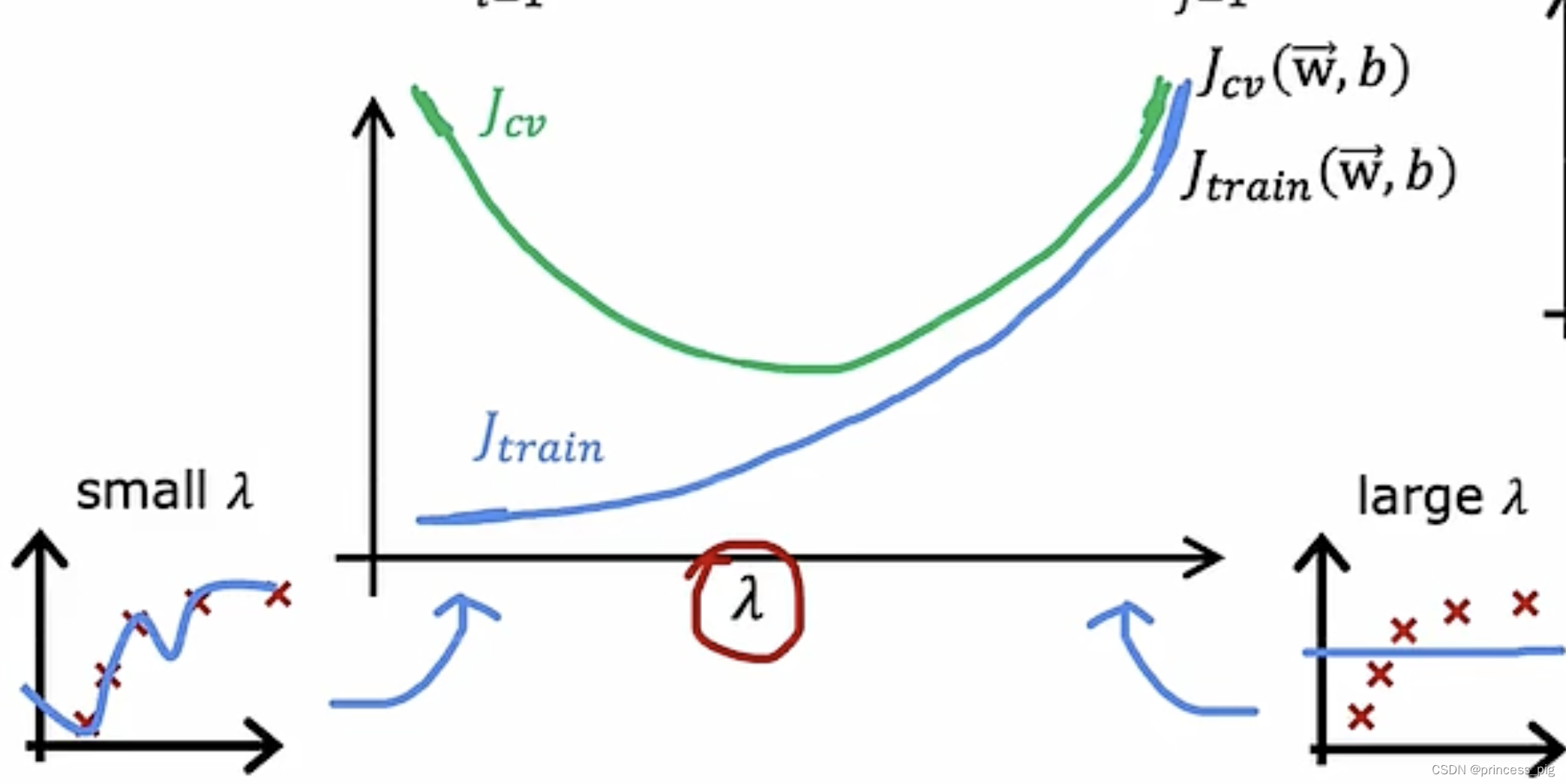
这是 $\lambda$ 与我们Jtrain和Jcv的关系，我们可以看到当我们的 $\lambda$ 过大时，我们的Jtrain会很大，而我们的Jcv也会很大，这部分被我们叫做偏差过大，而在 $\lambda$ 过小时，我们的Jtrain会偏小，而我们的Jcv还是偏大，这部分叫方差过大，也就是过拟合的情况。和之前的次数一样，我们需要找到一个中间值，才能找到一个合适的 $\lambda$ 。

基准值：

我们可以通过我们的基准值来判断我们的Jtrain和Jcv的大小，第一列中，训练误差远小于我们的交叉验证误差，所以第一个是过拟合(high variance)，而第二个是我们的训练误差远大于我们的交叉验证误差，所以它是高偏差(high bias)。

基准值是我们想要达到一个目标，它在不同的情况下，它的取值也并不一样。如果是0%，那你的要求就是完美，一般对于语音识别来说，会有10%的误差存在。

甚至会有两个误差都很大的情况出现。

学习曲线(learning curve)：

第一个特点，在我们的交叉验证误差，会随着我们的训练项的变大而减小，但是我们会发现我们的训练误差会变大，因为我们的曲线需要去拟合更多的数据，这就会导致我们的训练误差变大。可以看我们的右边的图片。但我们的交叉验证误差还是大于我们的训练误差。

第二个特点，随着训练集的数量上升，我们的Jcv和Jtrain会趋于平行，因为训练集越到后面，他们所处的位置与之前的都差不到，导致我们的平均误差也没有发生变化。

那当我们是高方差的情况下（过拟合）：

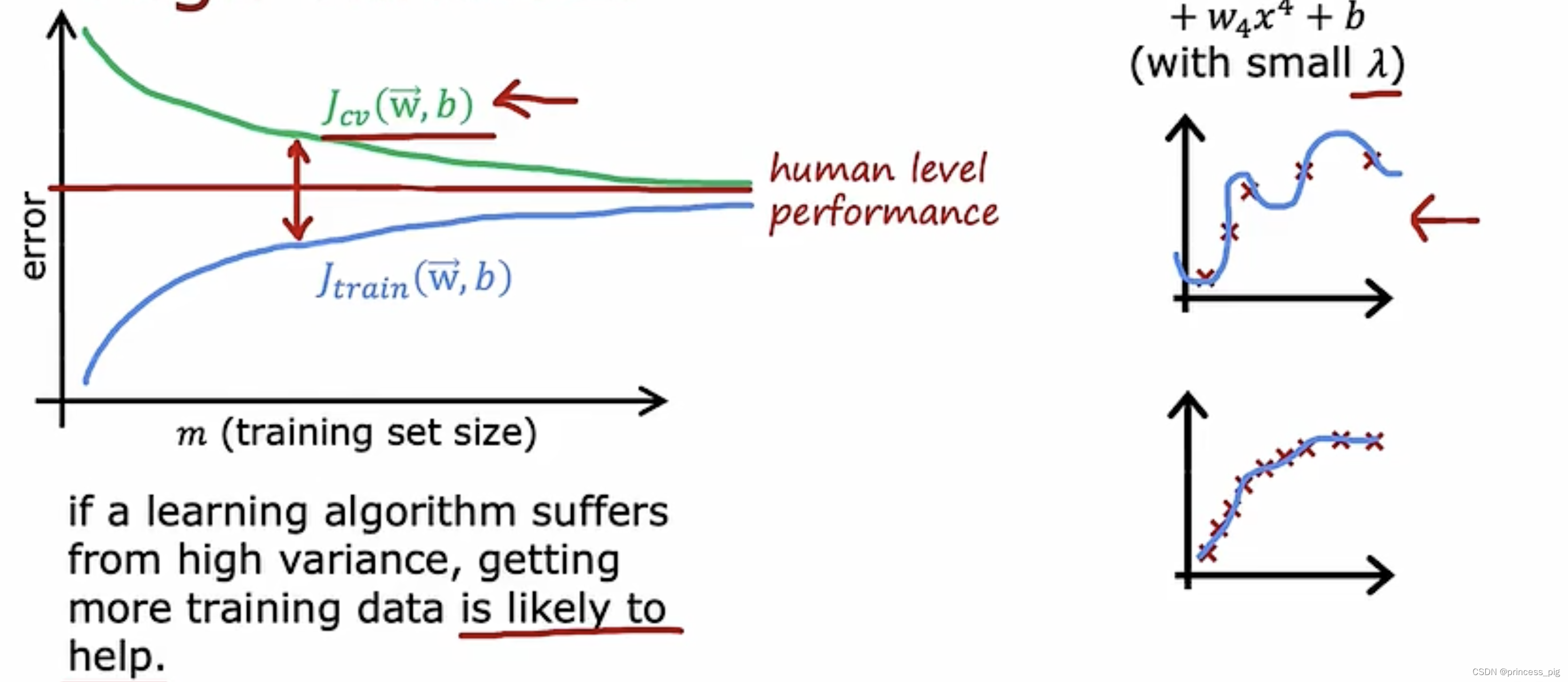
随着我们的训练集的增加，我们会看到我们的Jcv大于我们的人类的水平，而我们的Jtrian会出乎意料的低于我们的人类水平，因为他们是过拟合的，并且他们与交叉验证误差的差值也很大，但是随着我们的训练集的不断增大，我们的两个误差也会不断的向人类的水平靠近。我们可以看一下我们右边的两个图，上面那个图是我们的过拟合的图，而下面的则是我们根据数量的增加，不断接近的一个合适的函数，而不是过拟合的函数。

这个方法的唯一缺点就是我们需要使用大量的数据，计算是非常昂贵的。

我们可以来对应一下解决高方差和高偏差的方法：

可以好好想想为什么是这样。

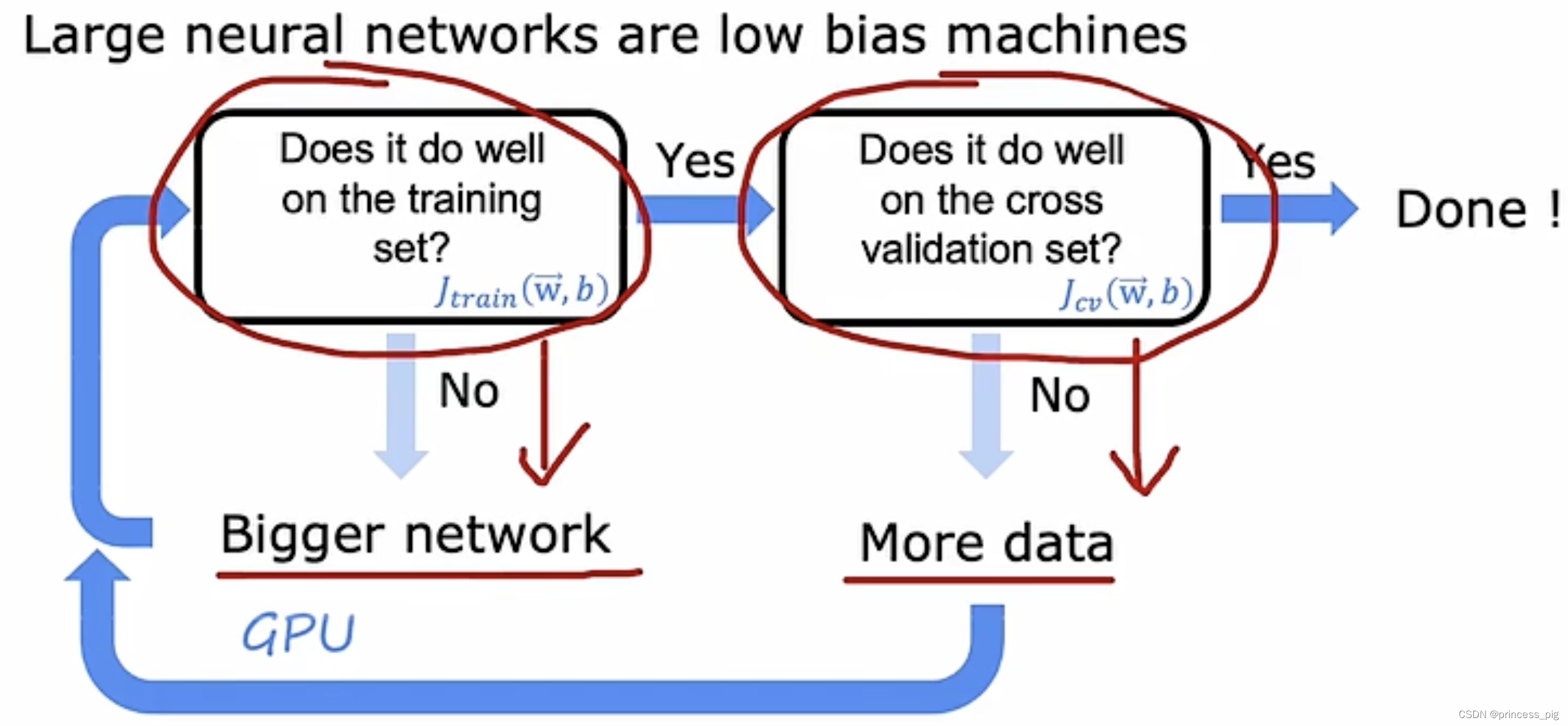
下图是我们如何做到，我们的神经网络足够的适合，我们完成一个神经网络，我们会对我们的训练误差先进行分析，如果接近或等于0，我们就进行到交叉验证分析。如果训练误差较大，那我们就应该去给我们的神经网络增加更多的特征，也就是创建更大的神经网络，再进行我们的训练误差的检验。当我们来到计算交叉验证误差处，偏大则是我们需要更多的数据，并重新会到训练误差处，重新开始以上的操作，而当我们的交叉验证误差也很小时，这一个神经网络就是一个比较好的神经网络了。

当然我们要对我们的神经网络正则化，也需要在每个神经网络层上加入正则化。

from tensorflow.keras.regularizers import L2
model = Sequential([ Dense(units=900, activation="relu", kernel_regularizer=L2(0.01)),Dense(units=500, activation="relu", kernel_regularizer=L2(0.01)),Dense(units=1, activation="linear", kernel_regularizer=L2(0.01))
])

这里的0.01指的是我们正则化的 $\lambda$ 值。