算法中的数学知识

约数

---

约数个数

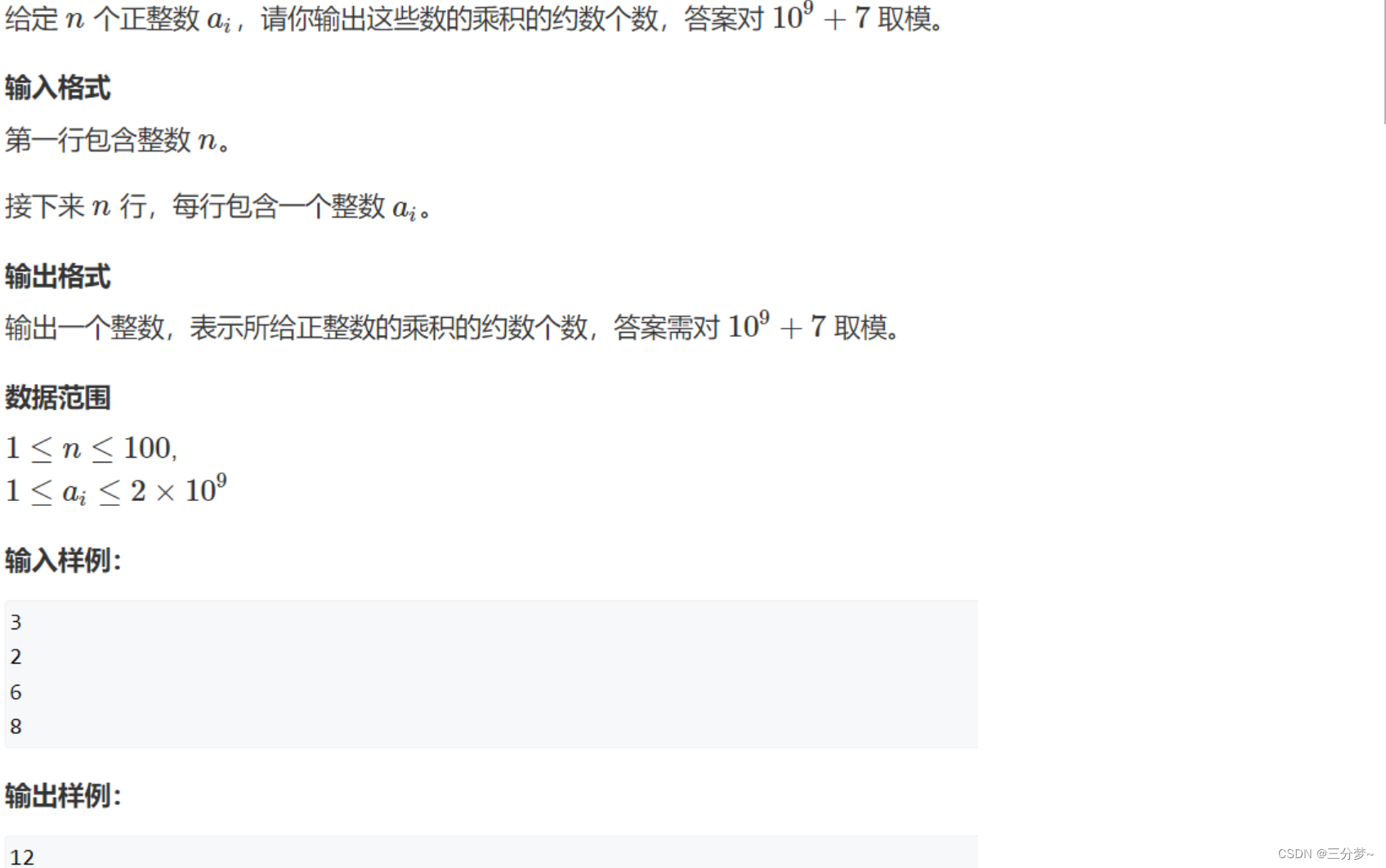
原题链接：约束个数

代码如下:

#include <iostream>
#include <unordered_map>
#include <algorithm>
using namespace std;
const int N = 110, mod = 1e9 + 7;
int main() {int n;cin >> n;unordered_map<int, int> primes; //分别存储质因子的底数和指数while(n--) {int x;cin >> x;for(int i = 2; i <= x / i; i++) {while(x % i == 0) {x /= i;primes[i]++;}}if(x > 1)   primes[x]++;}long long res = 1;for(auto prime : primes)    res = res * (prime.second + 1) % mod;cout << res;return 0;
}

---

约数之和

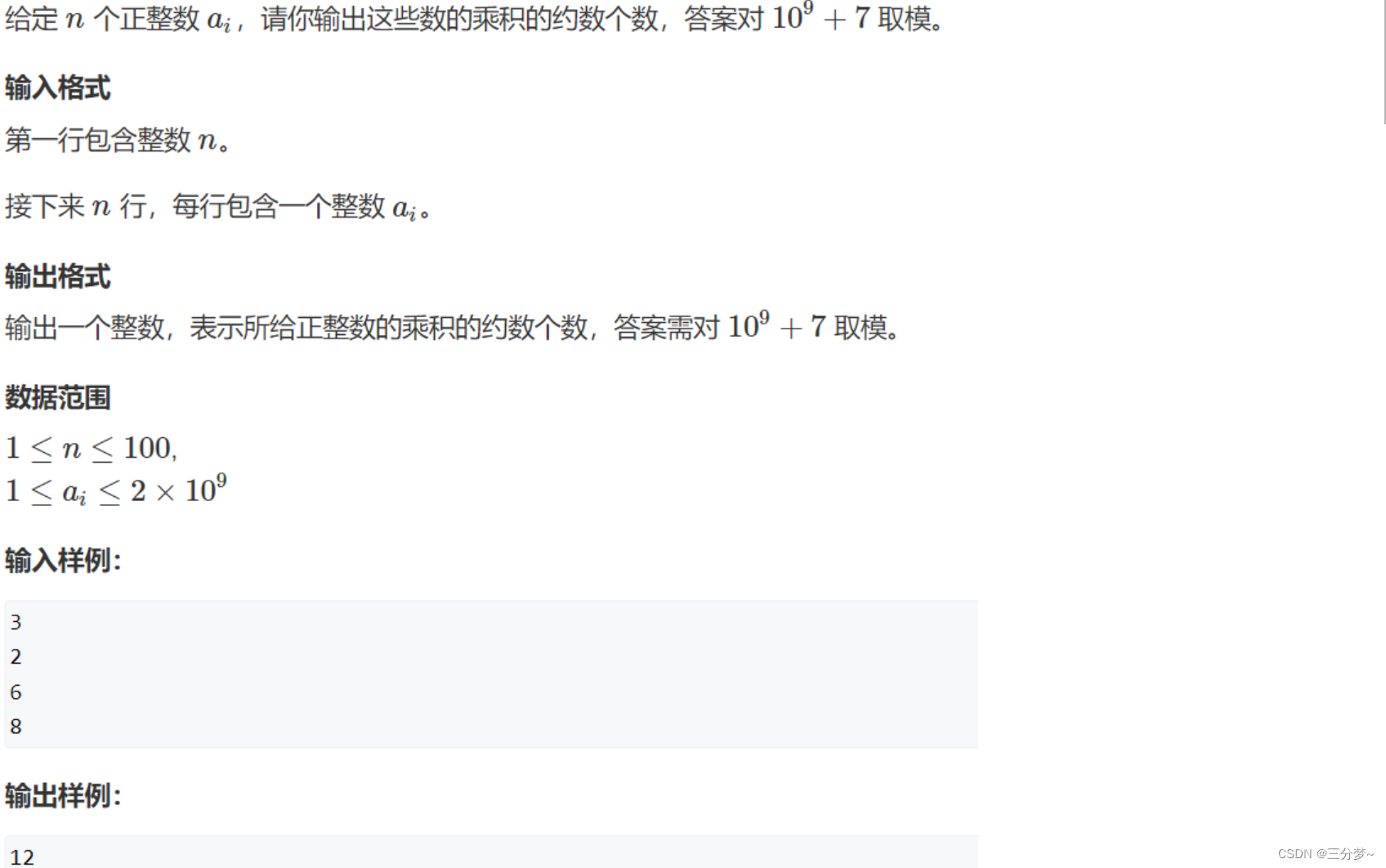
原题链接：约数之和

代码如下：

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
int main() {int n;cin >> n;unordered_map<int, int> primes;while(n--) {int x;cin >> x;for(int i = 2; i <= x / i; i++) {while(x % i == 0) {x /= i;primes[i]++;}}if(x > 1)   primes[x]++;}long long res = 1;for(auto prime : primes) {long long t = 1;while(prime.second --)t = (prime.first * t + 1) % mod;res = res * t % mod;}cout << res;return 0;
}

---

筛法求质数

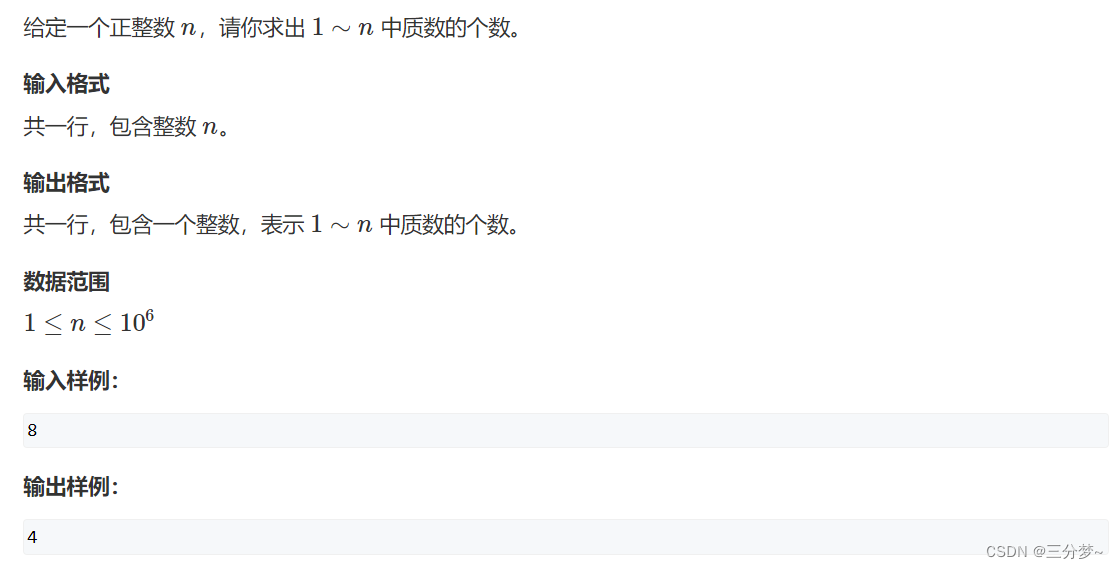
原题链接：筛质数

每次从最小质数开始遍历，可以保证n只会被最小质数筛到， 避免多次筛到， 每个数只会被筛一次， 即时间复杂度为$O(n)$， 线性筛法

#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int primes[N];
bool st[N];
int n;
int get_primes(int n) {if(n < 2)   return 0;int cnt = 0;for(int i = 2; i <= n; i++ ) {	//一次线性筛选，即可完成操作if(!st[i]) primes[cnt++] = i;	//没被筛到，则为质数for(int j = 0; primes[j] * i <= n; j++) {st[primes[j] * i] = true;	//从最小质数集开始筛选相关合数if(i % primes[j] == 0)  break;	//找到最小质因数，直接操作结束}}return cnt;
}
int main() {cin >> n;cout << get_primes(n);return 0;
}

---

阶乘分解

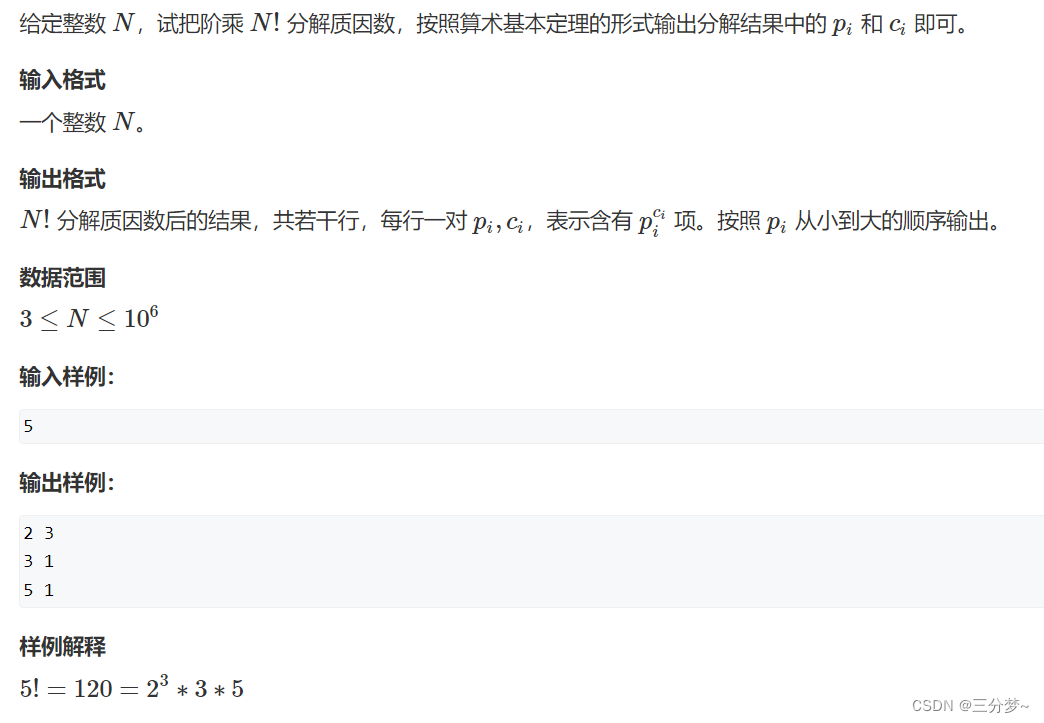
题目链接：https://www.acwing.com/problem/content/description/199/

解法一

思路分析：

先用线性筛法求出质数数组，随后对每个质数进行操作

$ans={\sum }_{primes[i]}^n\frac{n}{p}+\frac{n}{p^2}+\frac{n}{p^3}+\dots$

代码

//思路：将质数最小到大进行枚举，直接通过“倍数”[n/p]来计算相应次数，然而[1,n]中
//有的数含的p的次数不止一次，故进行[n/p] + [n / p^2] + [n / p^3] + ...
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int primes[N], cnt = 0;
bool st[N];
void get_primes(int n) {for(int i = 2; i <= n; i++) {   //枚举1~n中的所有筛选质数if(!st[i])  primes[cnt++] = i;  //若没有被筛掉，则为质数for(int j = 0; primes[j] * i <= n; j++) {st[primes[j] * i] = true;if(i % primes[j] == 0)  break;}}
}int main() {int n;cin >> n;get_primes(n);  //先初始化primes数组//然后进行枚举各个质数算出次数for(int i = 0; i < cnt; i++) {int p = primes[i];  //质数int t = n, ct = 0;while(t) ct += t / p, t /= p;   //每次的t/=p，下一次就成了cnt += t/p^2printf("%d %d\n", primes[i], ct);}}

解法二：

思路同上

#include <bits/stdc++.h>
using namespace std;
int n;
bool prime(int x) {if (x == 2) return 1;for (int i = 2; i * i <= x; i++) if (x % i == 0) return 0;return 1;
}
int main() {scanf("%d", &n);for (int i = 2; i <= n; i++) {if (!prime(i)) continue;long long x = i; int ans = 0;while (x <= n) ans += n / x, x *= i;printf("%d %d\n", i, ans);}return 0;
}

欧拉函数

基本模板

原题链接：欧拉函数

---

#include <iostream>
#include <unordered_map>
using namespace std;
int euler(int x) {int res = x;for(int i = 2; i <= x / i; i++) {if(x % i == 0) {res = res / i * (i - 1);while(x % i == 0)    x /= i;}}if(x > 1)   res = res / x * (x - 1);return res;
}int main() {int n;cin >> n;while(n --) {int a;cin >> a;cout << euler(a) << endl;}return 0;
}

---

筛法求欧拉函数

原题链接

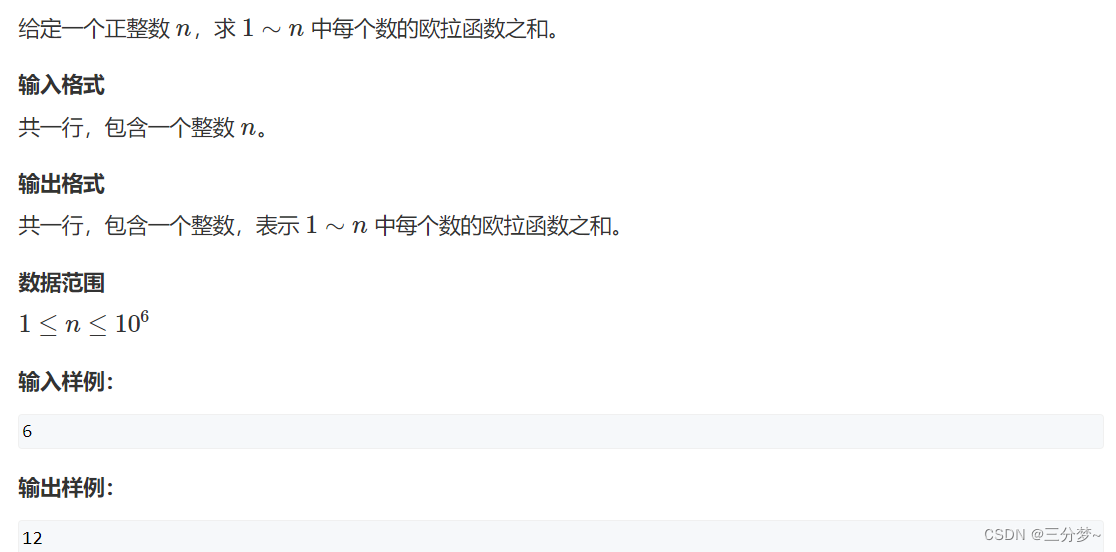
代码如下：

//欧拉：1 ~ n - 1 中与n互质的数的个数
#include <iostream>
#include <bitset>
using namespace std;
const int N = 1e6 + 10;
int primes[N], cnt;
int phi[N];
bitset<N> st;
long long get_eulers(int n) {long long res = 0;phi[1] = 1;for(int i = 2; i <= n; i++) {   //线性筛法，遍历一次nif(!st[i]) {    //没有被筛，质数primes[cnt++] = i;phi[i] = i - 1; //若为质数，则代表1 ~ i - 1都为互质}for(int j = 0; primes[j] <= n / i; j++) {st[primes[j] * i] = 1;if(i % primes[j] == 0)  {//若primes[j]为i的质因数，则有 primes[j] 的质因子必然存在于i中phi[i * primes[j]] = primes[j] * phi[i];break;}//若i % primes[j] != 0，则对质数primes[j]另行计算有:p[j] * (p[j] - 1) / p[j]phi[i * primes[j]] = phi[i] * (primes[j] - 1);}}for(int i = 1; i <= n; i++) res += phi[i];return res;
}
int main() {int n;cin >> n;cout << get_eulers(n); return 0;
}

大数据幂的欧拉函数

原题链接：互质数的个数

分析：

如上图可以将$\varphi (a^b)$分解为$a^b\ast \varphi (a)$， 继续演变为求欧拉和快速幂的结合应用

*** 代码如下：***

#include <iostream>
using namespace std;
const int MOD = 998244353;
long long qmi(long long a, long long b) {long long res = 1;while(b) {if(b & 1)   res = res * a % MOD;a = a * a % MOD;b >>= 1;}return res;
}
int main() {long long a, b;cin >> a >> b;if(a == 1) {    //题目要求是x不能取到a^b, 故如果a=1,互质个数为0cout << 0 << endl;return 0;}long long res = a, x = a;for(int i = 2; i <= x / i; i++) {if(x % i == 0) {res = res / i * (i - 1);while(x % i == 0)   x /= i;}}if(x > 1)   res = res / x * (x - 1);cout << res * qmi(a, b - 1) % MOD << endl;return 0;
}

​

快速幂

基本思想：

将$a^k$化为$$a^{2x1}\ast a^{2x2}\ast a^{2x3}\ast ...\ast a^{2xt}$$

***本质：***将k化为若干个2的次幂之和

这时候可以想到用二进制来操作

例如：若 k = 1101010 $<==>$ $2^1+2^3+2^5+2^6$

对二进制位数进行遍历， 当k & 1 == 1，即当前k的最后一个位置为1，进行累乘

代码如下：

#include <iostream>
using namespace std;
typedef long long LL;
// a^k % p
int qmi(int a, int k, int p) {int res = 1;//本质：将k拆分为2的n次幂之和while(k){ if(k & 1)   res = (LL)res * a % p;k >>= 1;a = (LL)a * a % p; }return res;
}int main() {int n;cin >> n;while(n-- ) {int a, b, p;scanf("%d%d%d", &a, &b, &p);cout << qmi(a, b, p) << endl;}return 0;
}

---

费马小定理

​

​ $$a^p与a在mod(p)的情况下是同余的$$

快速幂求逆元

快速幂求逆元

**分析：**只需求出$b^{p-2}\%p$的快速幂即可

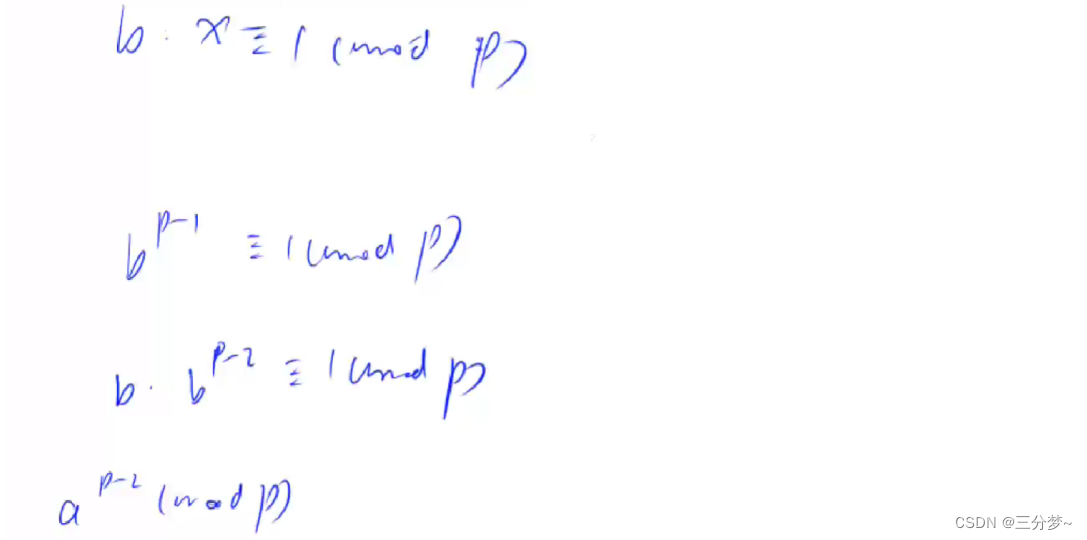
代码如下：

#include <iostream>
using namespace std;
typedef long long LL;int qmi(int a, int k, int p) {int res = 1;while(k) {if(k & 1)   res = (LL)res * a % p;k >>= 1;a = (LL)a * a % p;}return res;
}
int main() {int n;cin >> n;while(n-- ) {int a, p;scanf("%d%d", &a, &p);if(a % p == 0)  cout << "impossible" << endl;else cout << qmi(a, p - 2, p) << endl;}return 0;
}

数论分块

一般在算法中遇到时间复杂度为1e9的， 那么一次$O(n)$的遍历无法解决问题

求···${\sum }_{i=1}^n[\frac{n}{i}]$···

---

例题：因数平方和

分析:

要求$n$的约数，时间复杂度肯定不够， 所以想到反着求

a是b的约数 <==> b是a的倍数，所以我们只需要求哪些数包含约数a相加

每一个约数a 对答案的贡献度为$a^2$， 每个数a是$\frac{n}{a}$个数的约数

故a这个数对答案的总贡献为$a^2\ast [\frac{n}{a}]$，故答案为：
$$\sum _{i=1}^n[\frac{n}{i}]\ast i^2$$

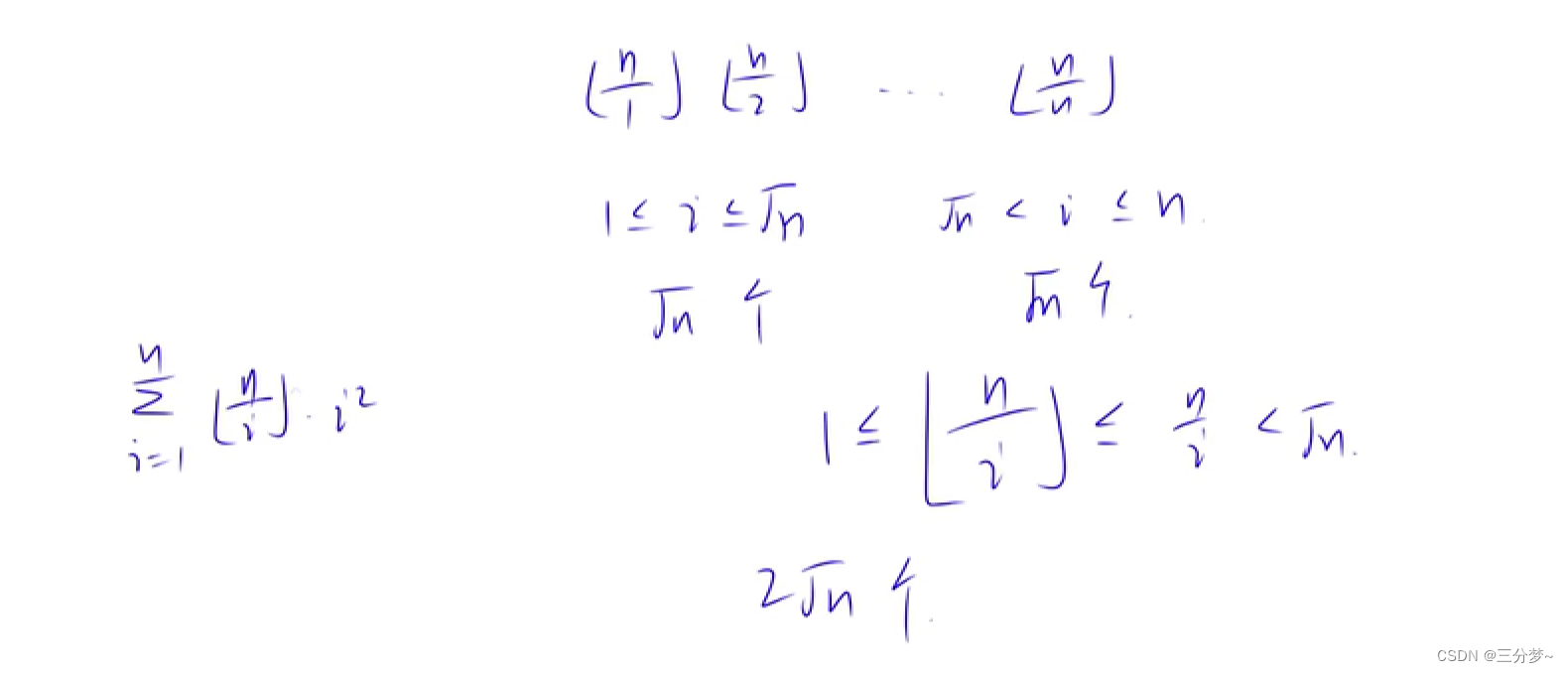
由上可知， 可以将n划分为前半段和后半段的话， 可计算出只需操作$2\sqrt{n}$个数即可

如此， 可以将$n$优化为$2\sqrt{n}$个数进行计算

进行分块治理，如下

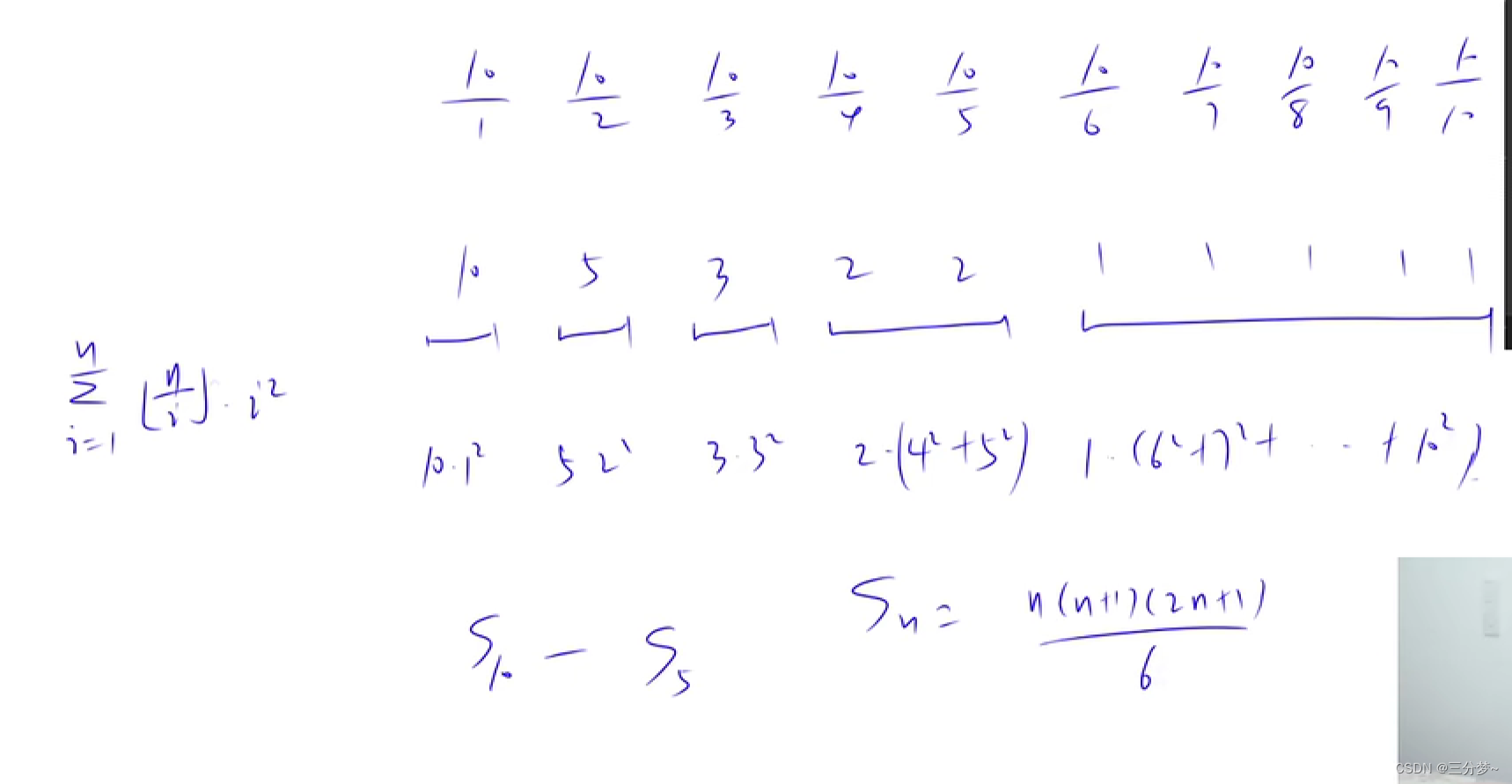
将区间长度为$n$划分为$2\sqrt{n}$个区间， 对每个区间进行求值，每个区间值相同， 只需算连续平方和，可以直接用公式求平方和值， 故每个区间只需要算一次即可

结果：$O(N)-->O(N^2)$

推导出：每个区间最大的位置：$y=n/x$ ， 对于各个区间值为==$x=n/i$==

即计算区间和每个==$[i,y]$区间即可， 然后算完一个区间直接 $i=y+1$，来跳跃到下一个区间进行计算， 总共只需要算$2\sqrt{n}$==次

具体代码：

此题在计算平方和时可能数据量会超大（超LL）

__int128写法

#include <iostream>
using namespace std;
const int MOD = 1e9 + 7;
typedef long long LL;
//__int128 : 2^127 - 1
LL calc(int n) {    //计算平方和
//这里可能特别大超过2^64(LL)，故用__int128临时存储数值return n * (__int128)(n + 1) * (2*n + 1) / 6 % MOD;   
}int main() {int n;cin >> n;LL res = 0;for(int i = 1; i <= n; ) {//划分为2sqrt(n)个区间，每个区间的所有数相等，第i个区间值为n/iint x = n / i, y = n / x;   //求区间[i, y]的平方和，再乘上x值res = res + x * (calc(y) - calc(i - 1)) % MOD;i = y + 1;  }//这块可能取模相减为负值，故cout << (res + MOD) % MOD << endl;return 0;   
}

---

逆元写法

LL calc(int n) {    //计算平方和
//这里可能特别大超过2^64(LL)，故用__int128临时存储数值// return n * (LL)(n + 1) * (2*n + 1) / 6 % MOD;   
//逆元写法return n * (LL)(n + 1) % MOD * (2*n + 1) % MOD * 166666668 % MOD;
}//计算 /6 的逆元
/for(int i = 1; ;i++) {		//算出逆元答案为166666668， 带入上式替换掉 '/6'if(i * 6 % MOD == 1) {cout << i << endl;return 0;}
}

例题2：余数之和

原题链接

思想：

首先看到数据范围为1e9级别，故可以想到用分块思想，优化到$O(2\sqrt{n})$

$k\%i$ <==> $k-[\frac{k}{i}]\ast i$

则$k\%{\sum }_1^n$ $<==>$ $n\ast k-{\sum }_{i=1}^n[\frac{k}{i}]\ast i$

代码：

#include <iostream>
using namespace std;
typedef long long LL;
LL sum_primes(int n, int k) {//k % i = k - [k / i] * i  --->   k % [1, n] = n*k - k / [1,n]*iLL res = (LL)n * k;for(int i = 1; i <= n; ) {if(k < i)   break;  //此时往后全为0，不用操作了int x = k / i, y = min(k / x, n);   //区间有极限值为n，防止越界//求区间总值 * x  --- > 等差数列求和：n * (a1 + an) / 2res -= x * (LL)(y - i + 1) * (i + y) / 2;i = y + 1;  //操作下一个区间}return res;
}
int main() {int n, k;cin >> n >> k;cout << sum_primes(n, k) << endl;return 0;
}

---

高斯消元法

基本性质：

1. 把某一行乘一个非$0$的数 (方程的两边同时乘上一个非$0$数不改变方程的解)

2. 交换某两行 (交换两个方程的位置)

3. 把某行的若干倍加到另一行上去 （把一个方程的若干倍加到另一个方程上去）

算法步骤

枚举每一列c

• 1. 找到绝对值最大的一行
• 2. 将该行换到最上面
• 3. 将该行第1个数变成1
• 4. 将下面所有行的第c列清成0

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 110;
double a[N][N];
int n;
const double eps = 1e-8;    //浮点型存在精度误差，容易
/*枚举每一列
- 1. 找到绝对值最大的一行 
- 2. 将该行换到最上面（第r行）
- 3. 将该行第1个数变成1
- 4. 将下面所有行的第`c`列清成0*/
int gauss() {int c, r;//首先开始枚举每一列进行“清零”操作for(c = 0, r = 0; c < n; c ++) {int mx_r = r;for(int i = r; i < n; i++)  //找到绝对值最大的一行if(fabs(a[i][c]) > fabs(a[mx_r][c]))mx_r = i;if(fabs(a[mx_r][c]) < eps)    continue;    //判断最大如果为0，那么没有算的必要for(int i = c; i <= n; i++) swap(a[mx_r][i], a[r][i]);  //换到第r行for(int i = n; i >= 0; i-- )    a[r][i] /= a[r][c]; //第”首位(c)“变为1for(int i = r + 1; i < n; i++ ) {// 将下面所有行的第`c`列清成0if(fabs(a[i][c]) > eps) //若是=0则没必要操作for(int j = n; j >= c; j--)a[i][j] -= a[i][c] * a[r][j];   //a[r][c]为1，故这样可以消0}r++;    //该方程式固定好，进行下一个方程式行的操作}//判断无解和无限解的情况if(r < n) { //这样的话，那么说明未知数方程式个数不足n，则无法构成完美梯形for(int i = r; i < n; i++ )if(fabs(a[i][n]) > eps) //多出的答案bi若是不等于0return 2;   //无解return 1;  //无限解    0 == 0}   //进行上三角矩阵的方程化简for(int i = n - 1; i >= 0; i -- ) { //从后往前，anxn = bn，一步一步推前方的方程式未知数for(int j = i + 1; j < n; j++)  //每i到最后只需保留第i个数(1),其它数全清零a[i][n] -= a[i][j] * a[j][n];   //这里第j行的答案已经算出，后续数（清零）的同步操作}return 0;   //有唯一解
}int main() {cin >> n;for(int i = 0; i < n; i++ )for(int j = 0; j < n + 1; j++ )cin >> a[i][j];int r = gauss();if(r == 0) {for(int i = 0; i < n; i ++) printf("%.2lf\n", a[i][n]);} else if(r == 1)   puts("Infinite group solutions");else puts("No solution");return 0;
}

组合数学

题型一

直接算的话会超时
考虑到只有2000 *2000个数，可以直接先打好表
$$C_a^b=C_{a-1}^{b-1}+C_{a-1}^b$$

代码

#include <iostream>
using namespace std;
const int N = 2010, MOD = 1e9 + 7;
int n;
int c[N][N];    //表示组合数C^b_avoid init() {for(int i = 0; i < N; i++ ) for(int j = 0; j <= i; j++) if(j == 0)  c[i][j] = 1;else c[i][j] = c[i - 1][j - 1] % MOD + c[i - 1][j] % MOD;
}int main() {cin >> n;init();while(n --) {int a, b;scanf("%d%d", &a, &b);printf("%d\n", c[a][b] % MOD);}return 0;
}

题型二

时间复杂度高，直接算不行，用集合状态的公式也不行
可以想到如何直接算出fact[N]的表然后套公式打表
$$C_a^b=\frac{a!}{(b!)\ast (a-b)!}$$
由于存在除法，数据量过大需要及时取模，而除法直接取模会导致答案变化，故想到求逆元（费马小定理+快速幂）然后进行相乘

---

代码如下

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 100010, MOD = 1e9 + 7;
int n;
int fact[N], infact[N]; //分别存储阶乘\阶乘的逆元
int qmi(int a, int b, int p) {int res = 1;while(b) {if(b & 1)   res = (LL)res * a % MOD;a = (LL)a * a % MOD;b >>= 1;}return res;
}
void init() {//0的阶乘/逆元阶都为1fact[0] = infact[0] = 1;for(int i = 1; i < N; i++) {fact[i] = (LL)fact[i - 1] * i % MOD;infact[i] = (LL)infact[i - 1] * qmi(i, MOD - 2, MOD) % MOD;}
}int main() {init();cin >> n;while(n-- ) {int a, b;scanf("%d%d", &a, &b);printf("%d\n", (LL)fact[a] % MOD * infact[b] % MOD * infact[a - b] % MOD);}return 0;
}

题型三（卢卡斯定理）

公式如下
$$C_a^b\equiv C_{amodp}^{bmodp}\ast C_{a/p}^{b/p}(modp)$$

推导

代码：

//发现a,b很大，而p很小，这种情况下用lucas定理来处理
#include <iostream>
using namespace std;
typedef long long LL;
int qmi(int a, int b, int p) {int res = 1;while(b) {if(b & 1)   res = (LL)res * a % p;a = (LL)a * a  % p;b >>= 1;}return res;
}
int C(int a, int b, int p) {if(b > a)   return 0;   //！边界条件int res = 1; // a!/(b!(a-b)!) = (a-b+1)*...*a / b!for(int i = 1, j = a; i <= b; i++, j--) {res = (LL)res * j % p;res = (LL)res * qmi(i, p - 2, p) % p;}return res;
}
int lucas(LL a,LL b, int p) {if(a < p && b < p)  return C(a, b, p);return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;//a%p后肯定是<p的,所以可以用C(),但a/p后不一定<p 所以用lucas继续递归
}
int main() {int n;cin >> n;while(n--) {int p;LL a, b;cin >> a >> b >> p;printf("%d\n", lucas(a, b, p));}return 0;
}

卡特兰数

889. 满足条件的01序列

题目链接：https://www.acwing.com/problem/content/891/

题目思路：

---

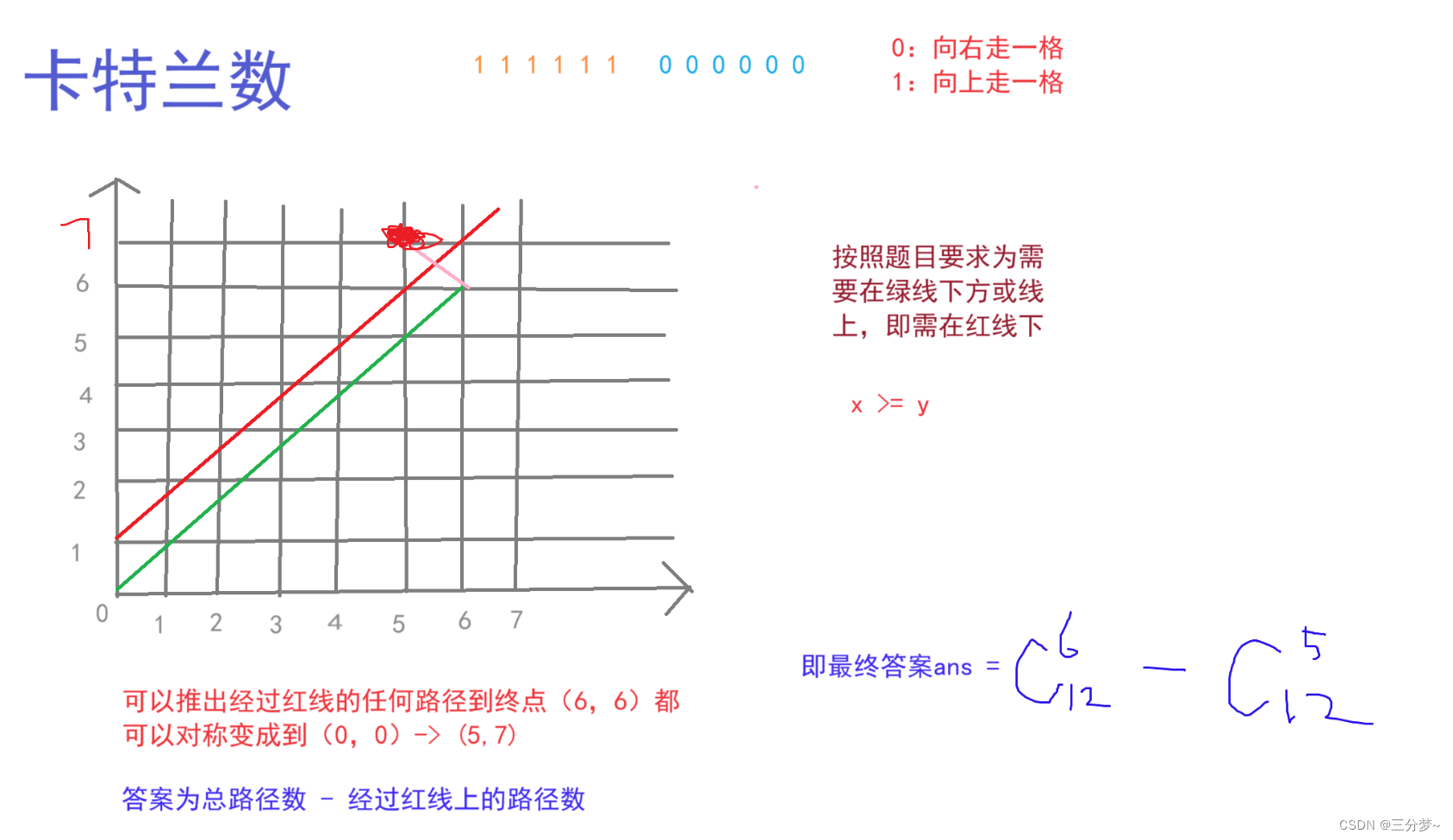
通过以上举例n=6时的情况，可以推出最终：
$$ans=C_{2n}^n-C_{2n}^{n-1}$$
又可化简为：
$$C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}$$
代码实现：

#include <iostream>
using namespace std;
const int MOD = 1e9 + 7;
typedef long long LL;
//用卡特兰公式: ans = (c^n_2n) / (n + 1)
int qmi(int a, int b, int p) {int res = 1;while(b) {if(b & 1)   res = (LL)res * a % p;a = (LL)a * a % p;b >>= 1;}return res;
}int main() {int n;cin >> n;int res = 1;// res = [(2n)! / (n! * n!)] / (n + 1)for(int i = 2 * n; i > 2*n - n; i--)    res = (LL)res * i % MOD;for(int i = 1; i <= n; i++) res = (LL)res * qmi(i, MOD - 2, MOD) % MOD;res = (LL)res * qmi(n + 1, MOD - 2, MOD) % MOD;cout << res;return 0;
} 

129.火车进站问题

原题链接：https://www.acwing.com/problem/content/131/

输入样例:

3

输出样例：

123
132
213
231
321

代码

#include <iostream>
#include <vector>
#include <stack>
#define end '\n'
using namespace std;
vector<int> path;
stack<int> stk;
int n, remain = 20;
void dfs(int u) {if(remain == 0) return ;if(path.size() == n) {remain --;  //剩余输出量for(auto t : path)cout << t;cout << endl;return ;}//两种操作选择//1. 出栈操作if(!stk.empty()) {  path.push_back(stk.top());stk.pop();dfs(u); //从1开始进行枚举//恢复操作stk.push(path.back());path.pop_back();}//2. 入栈操作if(u <= n) {stk.push(u);dfs(u + 1);//恢复操作stk.pop();}
}
int main() {cin >> n;dfs(1);return 0;
}

130.火车进出栈问题

原题链接：https://www.acwing.com/problem/content/132/