1.火柴排队

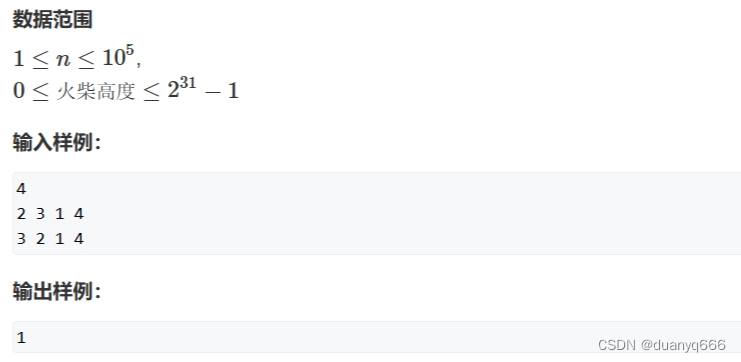
思路

1.求最小值的时候，可以直接按升序排序，这样得到的值就是最小值
2.求最小交换次数的时候，不能直接排序，因为只能交换相邻的数，只需要知道他们的相对大小，所以可以先用离散化，把火柴高度映射成 1 到 n，然后用一个中间数组 c，让 b 数组按照 a 数组的顺序归并排序，交换相邻两个元素，最多只会使得逆序对数量减一

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10, mod = 99999997;
int a[N], b[N], c[N], d[N];
int n;// 离散化 a 和 b 数组
void init(int q[]){for(int i = 1; i <= n; i++) d[i] = i;// d 数组根据 q 数组的大小关系排序sort(d + 1, d + n + 1, [&](int x, int y){return q[x] < q[y];});for(int i = 1; i <= n; i++) q[d[i]] = i;
}int merge_sort(int l, int r){if(l >= r) return 0;int mid = (l + r) / 2;int res = (merge_sort(l, mid) + merge_sort(mid + 1, r)) % mod;int x = 0, i = l, j = mid + 1;while(i <= mid && j <= r){if(b[i] <= b[j]) d[x++] = b[i++];else{d[x++] = b[j++];res = (res + mid - i + 1) % mod;}}while(i <= mid) d[x++] = b[i++];while(j <= r) d[x++] = b[j++];for(int i = l, j = 0; j < x; i++, j++) b[i] = d[j];return res;
}int main(){scanf("%d", &n);for(int i = 1; i <= n; i++) scanf("%d", &a[i]);for(int i = 1; i <= n; i++) scanf("%d", &b[i]);init(a), init(b);//for(int i = 1; i <= n; i ++ ) cout<<a[i]<<" ";//cout << "a" << endl;//for(int i = 1; i <= n; i ++ ) cout<<b[i]<<" ";//cout << "b" << endl;// c 数组做为中间数组，使得 a 数组是 "有序的"，让 b 数组按照 a 数组的顺序进行归并排序for(int i = 1; i <= n; i++) c[a[i]] = i;for(int i = 1; i <= n; i++) b[i] = c[b[i]];//for(int i = 1; i <= n; i ++ ) cout<<b[i]<<" ";//cout << "b" << endl;// 让 b 数组按照 a 数组的顺序进行归并排序int res = merge_sort(1, n);printf("%d", res);return 0;
}

2.归并排序

思路

模板题

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int n;void merge_sort(int l, int r){if(l >= r) return;int mid = (l + r) / 2;merge_sort(l, mid), merge_sort(mid + 1, r);int x = 0, i = l, j = mid + 1;while(i <= mid && j <= r){if(a[i] <= a[j]) b[x++] = a[i++];else b[x++] = a[j++];}while(i <= mid) b[x++] = a[i++];while(j <= r) b[x++] = a[j++];for(int i = l, j = 0; j < x; i++, j++) a[i] = b[j];
}int main(){scanf("%d", &n);for(int i = 0; i < n; i++) scanf("%d", &a[i]);merge_sort(0, n - 1);for(int i = 0; i < n; i++) printf("%d ", a[i]);return 0;
}

3.逆序对的数量

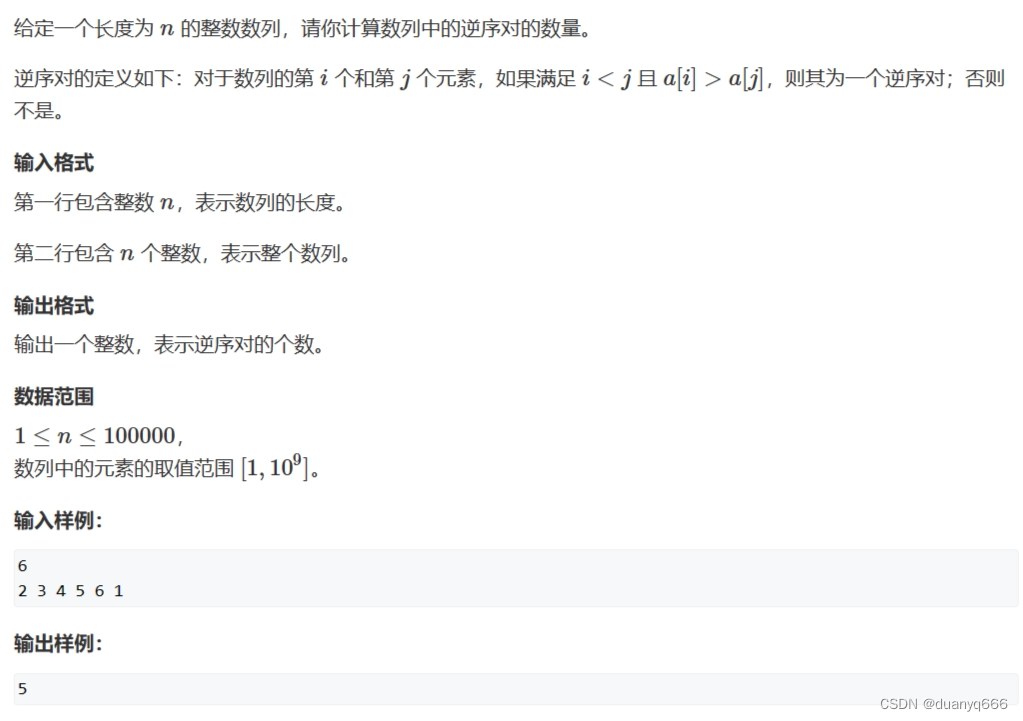
思路

模板题

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int n;
long long res;void merge_sort(int l, int r){if(l >= r) return;int mid = (l + r) / 2;merge_sort(l, mid), merge_sort(mid + 1, r);int x = 0, i = l, j = mid + 1;while(i <= mid && j <= r){if(a[i] <= a[j]) b[x++] = a[i++];else{res += 1ll * mid - i + 1;b[x++] = a[j++];}}while(i <= mid) b[x++] = a[i++];while(j <= mid) b[x++] = a[j++];for(int i = l, j = 0; j < x; i++, j++) a[i] = b[j];
}int main(){scanf("%d", &n);for(int i = 0; i < n; i++) scanf("%d", &a[i]);merge_sort(0, n - 1);printf("%lld", res);return 0;
}

4.小朋友排队

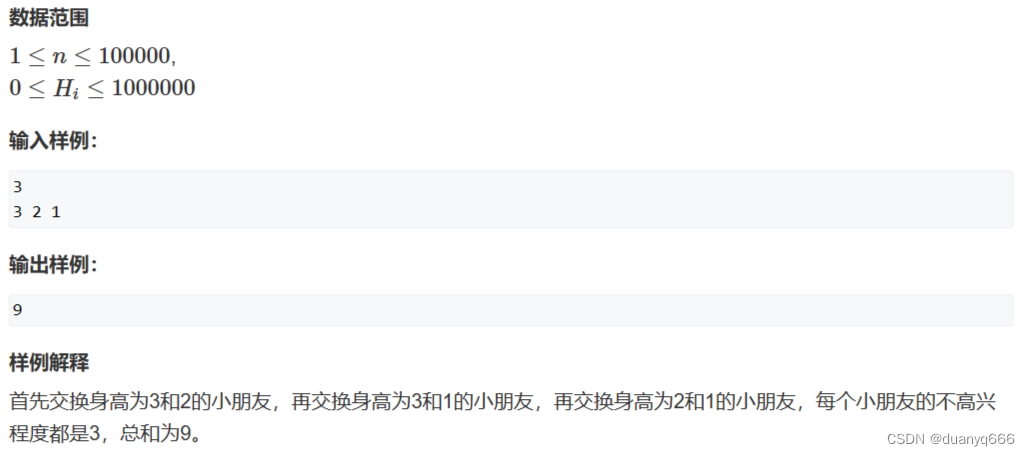
思路

k 队逆序对，最少交换次数就是 k，对于每个数，k1 表示左边有多少个比它大的，k2 表示右边有多少个比它小的，所有数的 k1 和 k2 加起来 >= 2 * k，最小就是 2 * k，也就是逆序对数量的两倍，所以一共交换 1 + 2 + 3 + … + k1 + k2，那么不高兴程度之和就是每个位置的 (1 + k1 + k2) * (k1 + k2) / 2 之和
小朋友要不停的换位置，所以要存储原来的下标

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
pair<int, int> a[N], b[N]; // 存储值和下标
long long sum[N];
int n;void merge_sort(int l, int r){if(l >= r) return;int mid = (l + r) / 2;merge_sort(l, mid), merge_sort(mid + 1, r);int x = 0, i = l, j = mid + 1;while(i <= mid && j <= r){// 加上后面比 a[i] 小的数if(a[i].first <= a[j].first){sum[a[i].second] += j - mid - 1;b[x++] = a[i++];}else{// 加上前面比 a[j] 大的数sum[a[j].second] += mid - i + 1;b[x++] = a[j++];}}while(i <= mid){sum[a[i].second] += j - mid - 1;b[x++] = a[i++];}while(j <= r) b[x++] = a[j++];for(int i = l, j = 0; j < x; i++, j++) a[i] = b[j];
}int main(){scanf("%d", &n);int x;for(int i = 0; i < n; i++){scanf("%d", &x);a[i] = make_pair(x, i);}merge_sort(0, n - 1);long long res = 0;for(int i = 0; i < n; i++) res += (1 + sum[i]) * sum[i] / 2;printf("%lld", res);return 0;
}

5.超快速排序

思路

逆序对的数量模板题

#include<iostream>
using namespace std;
const int N = 5e5 + 10;
int a[N], b[N];
int n;
long long res;void merge_sort(int l, int r){if(l >= r) return;int mid = (l + r) / 2;merge_sort(l, mid), merge_sort(mid + 1, r);int x = 0, i = l, j = mid + 1;while(i <= mid && j <= r){if(a[i] <= a[j]) b[x++] = a[i++];else{res += 1ll * mid - i + 1;b[x++] = a[j++];}}while(i <= mid) b[x++] = a[i++];while(j <= mid) b[x++] = a[j++];for(int i = l, j = 0; j < x; i++, j++) a[i] = b[j];
}int main(){while(scanf("%d", &n) && n){for(int i = 0; i < n; i++) scanf("%d", &a[i]);merge_sort(0, n - 1);printf("%lld\n", res);res = 0;}return 0;
}