1、数组理论基础

数组是存放在连续内存空间上的相同类型数据的集合。

需要两点注意的是

• 数组下标都是从0开始的。
• 数组内存空间的地址是连续的

因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

数组的元素是不能删的，只能覆盖。

二维数组在内存的空间地址是连续的么？

不同编程语言的内存管理是不一样的，以C++为例，在C++中二维数组是连续分布的。

2、二分查找

二分法的前提条件

• 有序数组
• 数组中无重复元素

二分法的两种写法

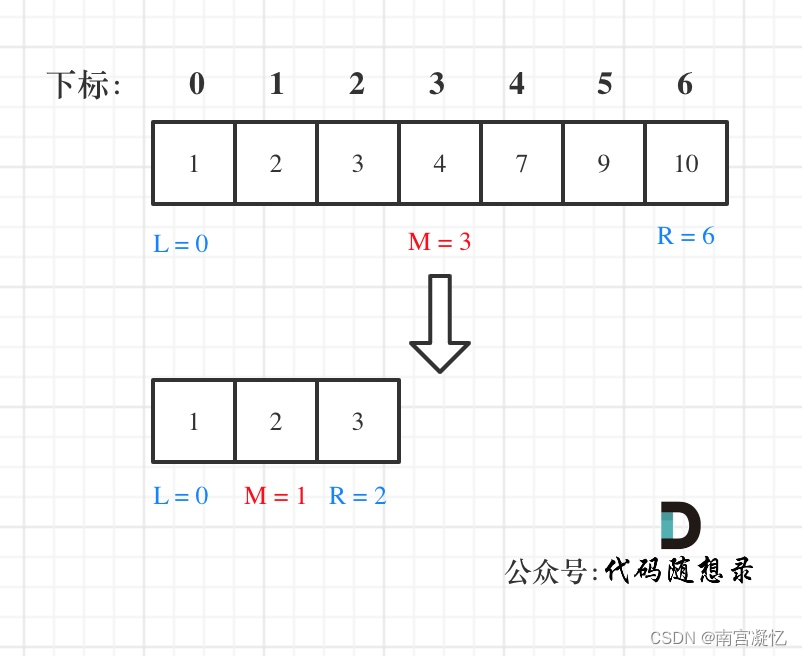
（1）定义 target 是在一个在左闭右闭的区间里，也就是[left, right]。

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

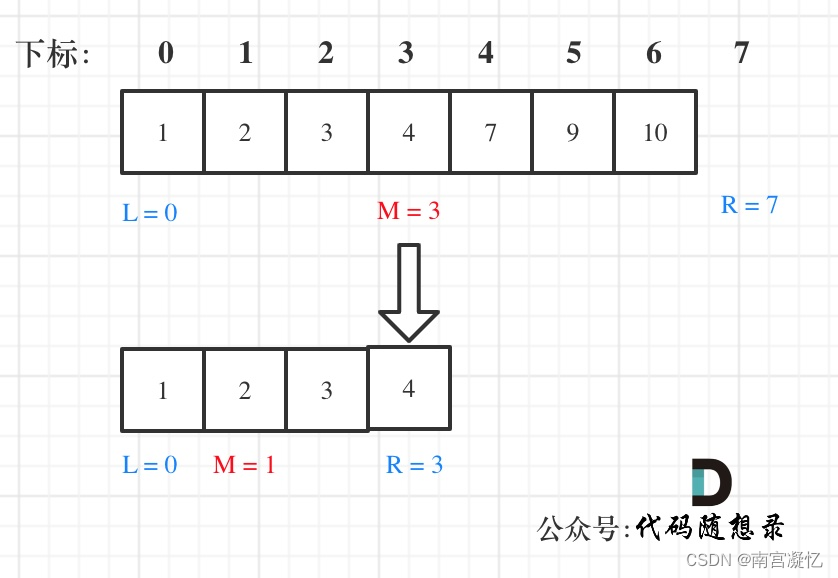
（2）定义 target 是在一个在左闭右开的区间里，也就是[left, right) 。

• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

3、移除元素

数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针

• 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
• 慢指针：指向更新 新数组下标的位置

很多同学这道题目做的很懵，就是不理解 快慢指针究竟都是什么含义，所以一定要明确含义，后面的思路就更容易理解了。

4、有序数组的平方

数组是有序的， 只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

感悟：

• 拿到数组，先找数值分布是否有规律，如果有规律，可以先从规律下手；
• 如果返回的数组大小是已知的，可以先定义并初始化好，后面修改里面的值就行。

5、螺旋矩阵 II

class Solution:def generateMatrix(self, n: int) -> List[List[int]]:number = nloop = n//2start_x, start_y = 0, 0 # 当前所在的行与列now = 0result = [[0]*n for _ in range(0,n)]i,j = 0,0 # 行列中的前进脚步flag = 1while(now < loop):while(j-now < n-1): # ➡result[start_x][j] = flagj += 1flag += 1start_y = jwhile(i-now < n-1): # ⬇result[i][start_y] = flagi += 1flag += 1start_x = iwhile(j > now): # ⬅result[start_x][j] = flagj -= 1flag += 1start_y = jwhile(i > now): # ⬆result[i][start_y] = flagi -= 1flag += 1now += 1start_x, start_y = now, nowi, j = now, nown = n-2if number%2 == 1:result[loop][loop] = number*numberreturn result