Python求均值、方差、标准偏差SD、相对标准偏差RSD

均值

均值是统计学中最常用的统计量，用来表明资料中各观测值相对集中较多的中心位置。用于反映现象总体的一般水平，或分布的集中趋势。

import numpy as npa = [2, 4, 6, 8]print(np.mean(a))  # 均值
print(np.average(a, weights=[1, 2, 1, 1]))  # 带权均值

方差

方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式：

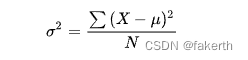
在这里插入图片描述
实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，样本方差计算公式：

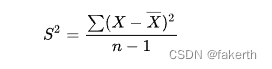
import numpy as npa = [2, 4, 6, 8]print(np.var(a))  # 总体方差
print(np.var(a, ddof=1))  # 样本方差

标准差SD

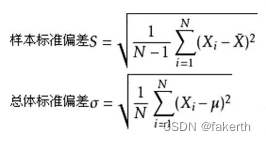
标准偏差(Std Dev,Standard Deviation) ，一种度量数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。

在这里插入图片描述

import numpy as npa = [2, 4, 6, 8]print(np.std(a))  # 总体标准差
print(np.std(a, ddof=1))  # 样本标准差

相对标准偏差RSD

相对标准偏差(relative standard deviation；RSD)又叫标准偏差系数、变异系数、变动系数等，由标准偏差除以相应的平均值乘100%所得值，可在检验检测工作中分析结果的精密度。

在这里插入图片描述

import numpy as npa = [2, 4, 6, 8]RSD = np.std(a, ddof=1)/np.mean(a)
print(RSD)

汇总

import numpy as npa = [2, 4, 6, 8]print(np.mean(a))  # 均值
print(np.average(a, weights=[1, 2, 1, 1]))  # 带权均值print(np.var(a))  # 总体方差
print(np.var(a, ddof=1))  # 样本方差print(np.std(a))  # 总体标准差
print(np.std(a, ddof=1))  # 样本标准差RSD = np.std(a, ddof=1)/np.mean(a)  # 相对标准偏差
print(RSD)

Numpy的数据离散程度度量

函数	功能
np.mean(list_a)	计算列表list_a的均值
np.average(list_a)	计算列表list_a的均值
np.average(list_a, weights = [1, 2, 1, 1])	计算列表list_a的加权平均数
np.var(list_a)	计算列表list_a的总体方差
np.var(list_a, ddof = 1)	计算列表list_a的样本方差
np.std(list_a)	计算列表list_a的总体标准差
np.std(list_a, ddof = 1)	计算列表list_a的样本标准差
np.median(list_a)	计算列表list_a的中位数
np.mode(list_a)	计算列表list_a的众数
np.percentile(list_a, (25))	计算列表list_a的第1四分位数
np.percentile(list_a, (50))	计算列表list_a的第2四分位数
np.percentile(list_a, (75))	计算列表list_a的第3四分位数
np.percentile(list_a, (25)) - np.percentile(list_a, (75))	计算列表list_a的四分位差
np.max(list_a) - np.min(list_a))	计算列表list_a的极差

四分位数

四分位数（Quartile）也称四分位点，是指在统计学中把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值。多应用于统计学中的箱线图绘制。它是一组数据排序后处于25%和75%位置上的值。四分位数是通过3个点将全部数据等分为4部分，其中每部分包含25%的数据。很显然，中间的四分位数就是中位数，因此通常所说的四分位数是指处在25%位置上的数值（称为下四分位数）和处在75%位置上的数值（称为上四分位数）。