① 打家劫舍

//不在栈内申请内存，防止溢出
int dp[101] = {0};
class Solution {
public:int rob(vector<int>& nums) {int sz = nums.size();//处理特殊情况if(sz == 1) return nums[0];else if(sz == 2) return max(nums[0], nums[1]);//先定义好前两个屋子，因为如果只有一个屋，答案就是它，如果两个屋，答案是比较大那个dp[0] = nums[0]; dp[1] = max(nums[0], nums[1]); for(int i = 2; i < sz; ++i) // sz = 3{//注释的部分是我第一遍写的代码，也确实是通过了全部用例，但比题解要复杂一些//这里通过遍历除了当前屋子紧挨的那屋前面所有dp状态找到能偷的最大值//但其实只用找dp[i - 2]就好了，所以多遍历了很多地方// int max = 0;// for(int j = 0 ; j < i - 1; ++j)// {//     if(max < arr[j]) max = arr[j];// }// arr[i] = nums[i] + max;//两个状态，要么不偷i这个屋子，偷的钱就是dp[i - 1]//要么就是偷i这个屋子，偷的钱就是i的钱数+dp[i - 2]dp[i] = max(nums[i] + dp[i - 2], dp[i - 1]);}//最大值出现在dp数组最后，直接返回即可return dp[sz - 1];}
};

② 删除并获得点数

仔细看完题目之后会觉得和打家劫舍非常相似，但是这里我们为了方便取出要利用到哈希算法，具体实现请看代码：

class Solution {
public:int deleteAndEarn(vector<int>& nums) {//处理特殊情况if(nums.empty()) return 0;else if(nums.size() == 1) return nums[0];int sz = nums.size();//找到整个数组中的最大值，以便创建哈希数组。int nums_max = nums[0];for(int i = 1; i < sz; ++i){nums_max = nums[i] > nums_max ? nums[i] : nums_max;}//向哈希数组中存储对应的个数，有一个就在对应位置加一vector<int> count(nums_max + 1);for(int i = 0; i < sz; ++i){count[nums[i]] += 1;}//最后这段是核心，也是理解动态规划的重点//题目中要求如果你删除掉了一个数获得了其积分，那么其紧邻的所有数都要被删除（没有积分）//因此在每次删除中你要么选择删除其紧邻的前一个数而放弃掉i所在位置的数//要么获得i所在数的全部积分以及i的上上个状态下的dp状态积分//也就是下面循环中单独那个语句的含义vector<int> dp(nums_max + 1);dp[1] = count[1] * 1;for(int i = 2; i <= nums_max; ++i){dp[i] = max(dp[i - 1],dp[i - 2] + i * count[i]);}//由于dp[0]不存东西，因此nums_max的位置是dp数组最后一位，也就是最大积分//（因为每一步都在寻找最大积分）return dp[nums_max];}
};

③ 不同路径

动态规划方程是每一个状态的路径数=其上面一个格子和左面一个格子的路径数之和，看代码👇

// 申请dp数组
int dp [110][110] = { 0 };
class Solution {
public:int uniquePaths(int m, int n) {for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j){// 初始化第一个格子if(i == 1 && i == j){dp[i][j] = 1;continue;} // 否则将当前格子上面和左面的格子的数字加起来就是结果dp[i][j] = dp[i-1][j] + dp[i][j-1];}}//返回dp数组最后一个位置的值（因为走到最后一个格子）return dp[m][n];}
};

④ 最小路径和

首先仍然只能往右走和往下走，然后给了个路径矩阵，让你找一个路径，使路径上数字和最小，代码👇

int dp[210][210] = {0};
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int row = grid.size();int col = grid[0].size();dp[1][1] = grid[0][0];for(int i = 1; i <= row; ++i){for(int j = 1; j <= col; ++j){//跳过第一格if(i == 1 && j == i) continue;//对于第一行的元素，除了首个元素，都只能从其左边右移得到//因此dp数组的当前状态应该是其左边的dp状态加上当前位置的值//这里grid都-1了是因为我是从i=1，j=1开始遍历的，对应grid中的位置要-1if(i == 1)dp[i][j] = grid[i - 1][j - 1] + dp[i][j-1];//对于第一列的元素，除了首个元素，都只能从其上面下移得到//因此dp数组的当前状态应该是其上面边的dp状态加上当前位置的值else if(j == 1)dp[i][j] = grid[i - 1][j - 1] + dp[i-1][j];//如果不在边上，那么就是上面格子和左面格子找个小的加上当前grid对应位置的值elsedp[i][j] = grid[i - 1][j - 1] + min(dp[i-1][j],dp[i][j-1]);}}//返回dp数组右下角元素return dp[row][col];}
};

⑤ 不同路径Ⅱ

和不同路径的区别就是多了个障碍，遇到障碍要绕开。

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int row = obstacleGrid.size();int col = obstacleGrid[0].size();vector<int> dp (col);//如果第一个位置就是障碍，直接就是0dp[0] = (obstacleGrid[0][0] == 0);for(int i = 0; i < row; ++i){for(int j = 0; j < col; ++j){if(obstacleGrid[i][j] == 1){//如果当前位置障碍是1，那么dp数组对应位置就是0dp[j] = 0;continue;}//若当前位置不是第一列并且当前位置无障碍，就根据其左侧和上侧状态求出dp[j]//而dp[j-1]就是(i,j)位置的左侧，被+=的dp[j]就是(i,j)位置的上侧//最后的+=结果就是(i,j)位置的新dp结果if(j > 0 && obstacleGrid[i][j] == 0)dp[j] += dp[j - 1];}}return dp.back();}
};

不理解滚动数组看看这里

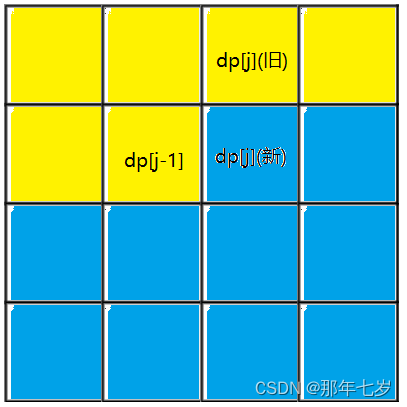
这里面涉及到一个滚动数组的概念。正常我们要设计二维dp来解决问题，但在此题目中，新路径数等于其dp矩阵中上面和左面的数字之和，如果换成一维数组，其左边的dp[j - 1]是刚好更新过的数字，那上面呢？上面是马上就要被覆盖的数字，就是+=之前的dp[j]！所以新的dp[j]就是原来的dp[j]加上刚刚左边更新的dp[j - 1]，就可以完成当前格子的更新。

⑥ 统计全为 1 的正方形子矩阵

此题重点仍然是理解dp推导的形式：
首先，dp矩阵的第一行和第一列直接copy原矩阵，是0就是0，是1就是1，因为在边上没办法组成边长大于一的正方形；
其次，除第一行和第一列外，如果矩阵中某个位置是0，那么与其对应的dp矩阵的相同位置也是0，因为包含此位置的情况是肯定组不成正方形的；
最后，也是最难理解的一点，假设dp数组dp[i][j]表示的是以(i, j)这个坐标为正方形右下角时正方形的最大边长，那么就可以认为最终的答案就是dp[i][j]这个二维dp数组中所有数之和（这里跳了很多步骤，讲解一下。因为每个正方形只有一个右下角格子，如果二维dp数组中存储的是以当前坐标格作为正方形右下角而算出来的能够形成正方形的个数，那么dp数组中每个格子所计算的个数都是不重复的[都有各自的右下角]，最后把他们加在一起，就能得到能形成的正方形的总数。至于为什么存储最大边长就能算出来个数，是因为假设dp[i][j] = 4，那么(i, j)这个坐标作为右下角就能够形成边长分别为1、2、3和4的四个正方形，不难看出，最大边长是几，就能以此坐标为右下角形成几个正方形，自然而然也就可以存入dp矩阵进而求和了。）

随后我们来进行递推：
假设包围(i, j)这个坐标的三个坐标(i - 1, j - 1)、(i, j - 1)、(i - 1, j)对应的f[i - 1][j - 1]、f[i][j - 1]、f[i - 1][j]中的最小值3，含义就是这三个坐标均可作为一个最大变长为3的正方形的右下角。前面我们已经说到了，如果矩阵中某个位置是0，那么与其对应的dp矩阵的相同位置也是0，所以如果(i, j)坐标的矩阵值是1，我们就不难发现，f[i][j]只能是4。我们用这个图举例子：

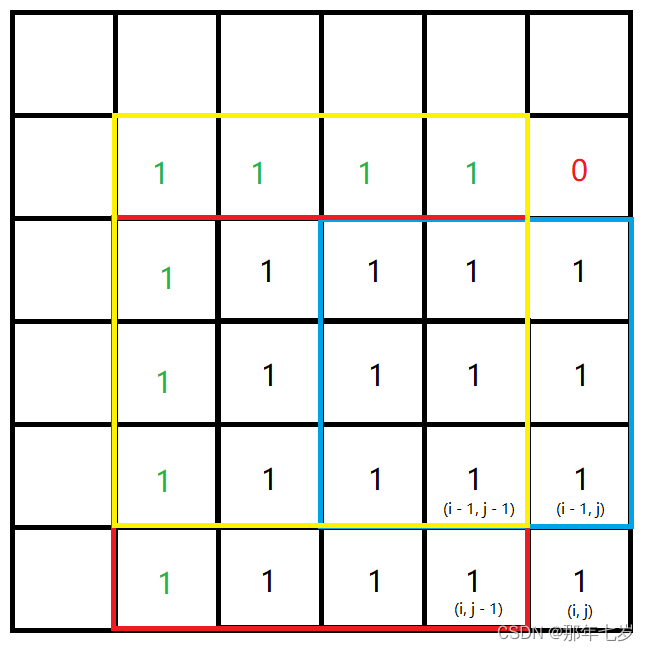
如果我们知道包围(i, j)这个坐标的三个坐标(i - 1, j - 1)、(i, j - 1)、(i - 1, j)对应的f[i - 1][j - 1]、f[i][j - 1]、f[i - 1][j]中的最小值3（红黄框为4，蓝框为3），那么加上(i, j)这个值为1坐标，我们只能得到边长为4的正方形，想小一点的话，这个4×4矩阵除了右下角全是1，除非这位置是0，不然就只能乖乖形成最大边长为4的右下角；想大一点的话，我们知道f[i - 1][j - 1]、f[i][j - 1]、f[i - 1][j]中的最小值3，你但凡在左侧和上侧各填一行，最少会添一个0，就不成立了。因此直接锁死递推式：

dp[i][j]=min(dp[i][j−1],dp[i−1][j],dp[i−1][j−1])+1 //伪代码，min函数最多接受两个参数

力扣给出的完整递推式如下：

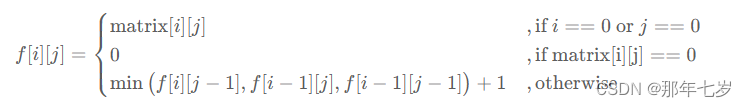
也是严格按照前面的步骤来的，第一行或者第一列直接赋值；原矩阵为0的位置，dp矩阵也为0；剩下的情况就是求左、左上、上的最小值再加1，就是当前坐标dp矩阵的结果。下面是实现代码👇

class Solution {
public:int countSquares(vector<vector<int>>& matrix) {int ret = 0;int row = matrix.size(), col = matrix[0].size();vector<vector<int>> dp(row, vector<int>(col,0));for(int i = 0; i < row; ++i){for(int j = 0; j < col; ++j){if(i == 0 || j == 0)dp[i][j] = matrix[i][j];else if(matrix[i][j] == 0)dp[i][j] = 0;elsedp[i][j] = min(min(dp[i - 1][j - 1],dp[i - 1][j]),dp[i][j - 1]) + 1;// 在循环最内层把dp矩阵中每一个元素进行累加，以求得结果ret += dp[i][j];}}return ret;}
};

⑦ 最大正方形

和上面的题思路完全一致，这次不是找到所有正方形了，就是单纯找到dp矩阵中的最大值，代码如👇：

class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {int length = 0;int row = matrix.size(), col = matrix[0].size();int pre = 0;//vector<vector<int>> dp(row, vector<int>(col, 0));vector<int> dp(col + 1);for(int i = 0; i < row; ++i){for(int j = 0; j < col; ++j){int temp = dp[j];if(i == 0 || j == 0)dp[j] = matrix[i][j] - '0';else if(matrix[i][j] == '0')dp[j] = 0;elsedp[j] = min(min(dp[j - 1],dp[j]),pre) + 1;pre = temp;length = length > dp[j] ? length : dp[j];}}return length * length;}
};

这里我们优化了空间，前面一道题的解法使用的是二维的dp矩阵，但是我们每部运算只需要当前位置左、上以及左上三个位置的数据。当我们在使用一维dp数组时，当前位置左侧的就是我们要的左侧，当前位置未更新前的数据就是我们要的上侧，所以我们只需要保存上一次计算中的左上的数据即可，因此引入pre和temp变量，每次pre保存的是这个循环计算前dp[j]的值，留用下次循环进行比较用，而temp则是直接保存计算dp值前的状态，在计算后赋给pre。