【洛谷 P8744】[蓝桥杯 2021 省 A] 左孩子右兄弟题解（深度优先搜索+贪心算法+树形DP+邻接表）-编程知识

【洛谷 P8744】[蓝桥杯 2021 省 A] 左孩子右兄弟题解（深度优先搜索+贪心算法+树形DP+邻接表）

[蓝桥杯 2021 省 A] 左孩子右兄弟

题目描述

对于一棵多叉树，我们可以通过“左孩子右兄弟”表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

给定一棵包含 $N$ 个结点的多叉树，结点从 $1$ 至 $N$ 编号，其中 $1$ 号结点是根，每个结点的父结点的编号比自己的编号小。请你计算其通过"左孩子右兄弟"表示法转化成的二叉树，高度最高是多少。（只有根结点这一个结点的树高度为 $0$ ）

例如如下的多叉树：

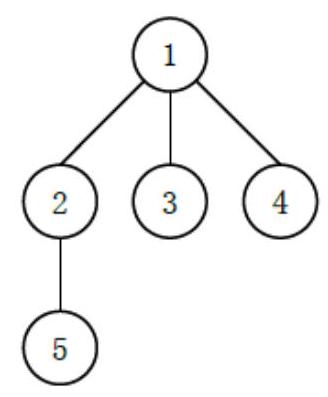
可能有以下 $3$ 种 (这里只列出 $3$ 种, 并不是全部) 不同的 “左孩子右兄弟” 表示:

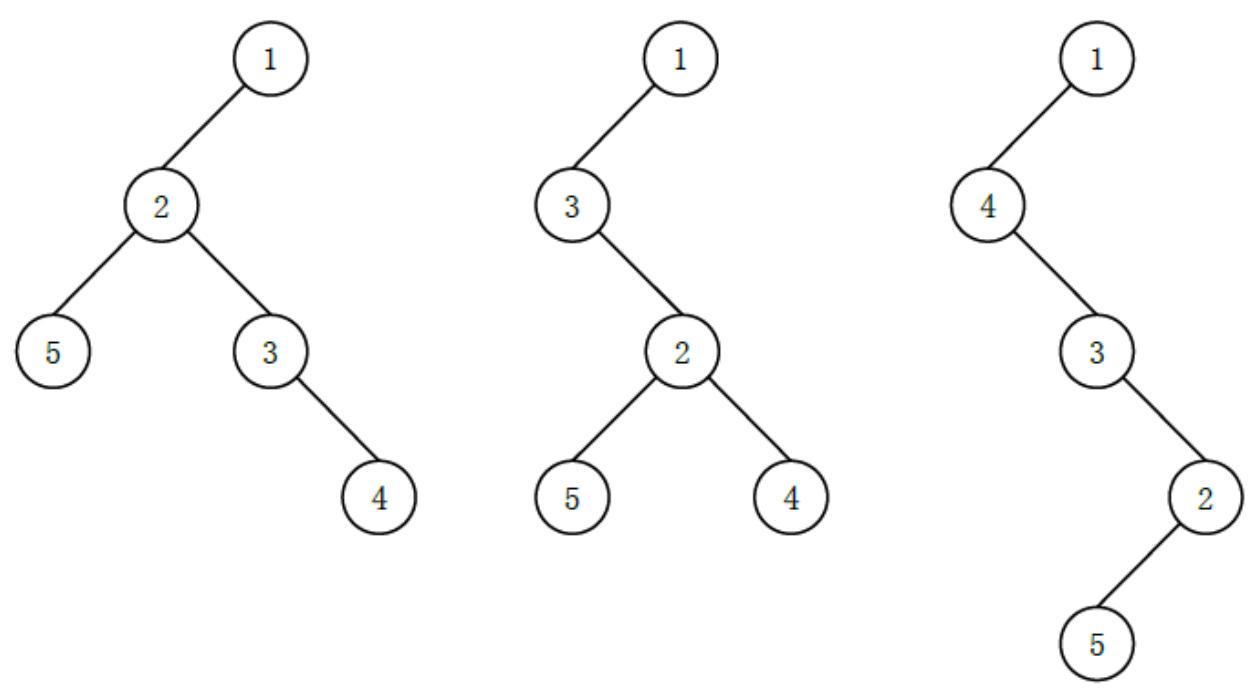
其中最后一种高度最高, 为 $4$ 。

输入格式

输入的第一行包含一个整数 $N$ 。

以下 $N - 1$ 行, 每行包含一个整数, 依次表示 $2$ 至 $N$ 号结点的父结点编号。

输出格式

输出一个整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

对于 $\%$ 的评测用例， $\leq N \leq 20$ ;

对于所有评测用例， $\leq N \leq 10^5$ 。

蓝桥杯 2021 第一轮省赛 A 组 H 题。

思路

首先，定义一个全局变量dp[N]，dp[i]存储的是节点i作为根的子树转化为二叉树后的最大高度。

定义一个全局的vector数组child[N]，用于存储每个节点的所有子节点。例如，child[i]存储的是节点i的所有子节点。

从输入中读取节点数量n，然后读取每个节点的父节点编号，并将当前节点加入到父节点的子节点列表中。

接下来，从根节点1开始进行深度优先搜索。在每个节点x处，遍历其所有子节点。

设 $d p [i]$ 表示节点 $i$ 作为根的子树转化为二叉树后的最大高度， $c$ 表示节点 $i$ 的子节点， $sz$ 表示节点 $i$ 的孩子数量。节点 $i$ 作为根的子树转化为二叉树后的最大高度等于该节点孩子的数量加上孩子节点中作为根的子树转化为二叉树后的最大高度。状态转移方程为：

$max_{c \in child[i]}(dp[c])$

对每个子节点i，先通过递归调用dfs(i)进行深度优先搜索，然后更新dp[x]为dp[x]和dp[i]中的最大值。最后，将节点x的子节点数量sz加到dp[x]上，因为每个子节点都可以作为一个新的层级添加到二叉树中。

最后，输出dp[1]，即根节点作为根的子树转化为二叉树后的最大高度，即为所求的二叉树的最大高度。

AC代码

#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
#define mp make_pair
#define AUTHOR "HEX9CF"
using namespace std;
using ll = long long;const int N = 1e6 + 7;
const int INF = 0x3f3f3f3f;
const ll MOD = 1e9 + 7;int n;
ll dp[N];vector<int> child[N];void dfs(int x) {int sz = 0;for (const auto i : child[x]) {// 访问孩子dfs(i);sz++;dp[x] = max(dp[x], dp[i]);}dp[x] += sz;
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);memset(dp, 0, sizeof(dp));cin >> n;for (int i = 2; i <= n; i++) {int fa;cin >> fa;child[fa].push_back(i);}dfs(1);cout << dp[1];return 0;
}