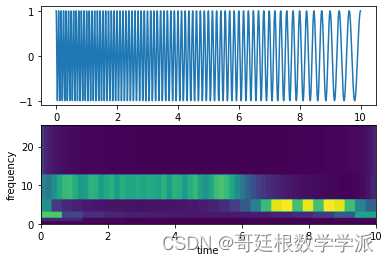
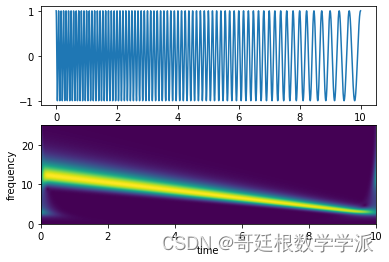
Python环境下一维时间序列的Stockwell变换(原始S-transform 和快速离散标准正交S-transform)。
Stockwell变换是连续小波变换思想的延伸,并且使用的是一个可移动的,可伸缩的高斯窗函数。它具有连续小波变换所不具有的一些有价值的性质。Stockwell变换的特别之处在于它具有很好地频率相关分辨率,同时它与傅里叶变换有直接的关联。Stockwell变换最初是用在地震波的分析处理中的。在地理数据分析及其他学科领域,平稳信号只是一种理想化的数学模型,很难实现并且在信号分析中用处不大。尽管傅里叶变换包含整个时间序列的频谱信息,但是对于大多数实用信号来说,傅里叶变换所体现的信息是不够的。例如,地震波信号。这些时间序列的频谱成分与时间有很大的相关性,因此,地震波信号的分析需要联合时域分析,这时Stockwell变换因其时频分布具有频率相关的分辨率而被提出。
再以脑电信号为例,由于脑电信号同样是时变非平稳信号,其频谱中含有大量的生理和病理信息,分析正常脑电信号与异常脑电信号的频谱对于自动癫痫检测具有重要的意义。因此,可以将Stockwell变换类比于地震波信号尝试用于脑电信号的分析。传统的用于脑电信号分析的时频分析方法包括短时傅里叶变换、小波变换、维格纳-维利分布等。短时傅里叶变换通常被用于非平稳、多成分的信号。由于它使用的是固定的窗函数,因此无法在高频提供好的时间分辨率、低频提供好的频率分辨率。尽管小波变换能够克服短时傅里叶变换的缺陷,但同时失去了局部频率之间的联系。维格纳-维利分布分布提供了一个高的时间与频率分辨率,但是由于其双线性的特性导致交叉项干扰的存在。Stockwell变换结合了时频相位的频率相关分辨率以及绝对引用局部相位信息。
Stockwell提供了很高的频率相关分辨率,当频率增大时,Stockwell变换的窗函数就会变小,因此它具有良好的频率局域化特性:低频处有出众的时频分辨率,高频处有高的时间分辨率。由于其良好的线性性质,附加噪声也可很容易去除。由于Stockwell变换结合了短时傅里叶变换的特性及小波变换的优点,因此它成为非平稳信号特征提取的一个理想的方法。
该代码为一维时间序列信号的Stockwell变换,包括原始Stockwell变换和快速离散标准正交Stockwell变换,运行环境为Python,部分代码如下:
# parameter:
# data——numpy.ndarray , the origion 1-D signal
# minfreq——int , the minimum frequence in result
# maxfreq——int , the maximum frequence in result
# samprate——int , the time interval of origion signal
# freqsamprate——int , the frequence interval in result
# remove_edge——boolean , remove a least-squares fit parabola and put a 5% hanning taper on origion signal
# analytic_signal——boolean , turn the real_value signal into analytic signal and then start s-transform
# factor——int , the width factor of localizing gaussian window: factor=1 —— original S transform
# factor≠1 —— generalized S transform(GST)
#
# For simple use ———— if you have 500 points of 50Hz singal,you want check 10-30Hz frequency domain
# then set st(data,minfreq=100,maxfreq=300)
#import numpy as np
from scipy import signal
import sys
import copy完整代码:https://www.toutiao.com/article/7346036982370419226/
出图如下: