SAT和SMT介绍及求解器使用-编程知识

一、SAT

1、介绍

（1）定义

SAT即命题逻辑公式的可满足性问题/布尔可满足性问题。即给定一个与或非和变量组成的命题公式，判断是否存在一些结果使得这个公式成立

它是第一个被确认为NP完全的问题。

输入：析取范式（CNF）
输出：布尔值，代表是否可满足（SAT/UNSAT）

以演讲是否需要打领带的例子，说明它有几个组成部分：

布尔变量/文字(literal)：tie(领带)，shirt(衬衫)
符号：~(非)、∧(与)、 ∨(或)
子句(clause)-析取式
- 演讲不能只打领带，不穿衬衫： _(tie∧shirt) → ~ tie ∨ shirt
- 演讲不能既不打领带，也不穿衬衫： ₍ tie∧~shirt) → tie ∨ shirt
- 自己不喜欢既打领带，又穿衬衫： ~(tie∧shirt) → ~ tie ∨ ~ shirt
约束/公式-合取式： (~ tie ∨ shirt) ∧ (tie ∨ shirt) ∧ (~ tie ∨ ~ shirt)

由文字和符号组成子句。经过变换，子句构成完整约束。则SAT求解器的输入是3个子句。

（2）求解思路

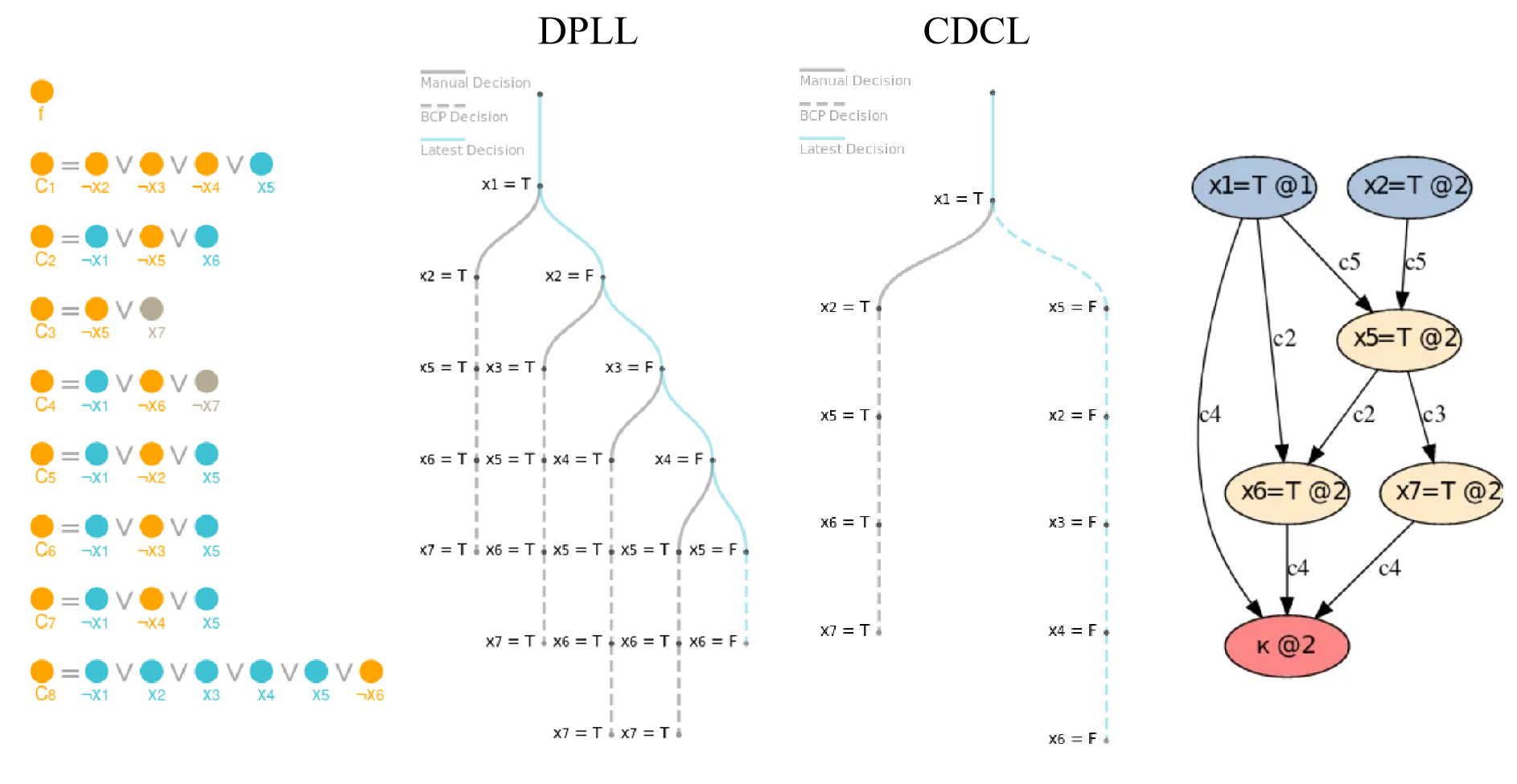
SAT的求解过程可以划分成两个阶段：第一阶段是布尔约束传播/子句传播，第二阶段是冲突分析，可以采用递归回溯(DPLL算法)或冲突子句学习(CDCL算法)。

求解过程及两个算法的差异可以在网站 https://cse442-17f.github.io/Conflict-Driven-Clause-Learning/ 上看到可视化效果。

a）布尔约束传播

子句传播就类似在做数独游戏时，在某个空格填入某一个数字之后，就会排除掉一些其它空格内数字的选项，从而减少尝试赋值的次数。如果这个过程推出一个值为假的子句，我们称为『发生冲突』。如果发生冲突，就像是走迷宫，要退回上一个岔路口，选择一条不同的路再继续走。它的运行思路如下：

对一个文字赋值后，以此为条件进一步给其他文字赋值（BCP）
- 未发生冲突，尝试为下一个赋值。
- 直到所有变量均赋值且没有冲突 → SAT
发生冲突，回溯

但这个过程也有可能在退到上一个路口后又来到同一个死胡同，我们希望找到可以避开死胡同的岔路。这就来到冲突分析环节。

b）冲突分析

递归回溯(DPLL算法)

冲突回溯也会产生两个结果：回溯到了首次赋值，这意味着这个问题横竖都是无法满足的，那么就可以宣告“UNSAT”；反之，则回溯到之前的某次赋值，撤销这次赋值之后的所有赋值，类似一个undo操作。这个就是比较经典的DPLL算法，但这样存在一些问题。一方面是，它遇到冲突的时候，只知道当前的部分赋值会导致冲突，除此之外学不到任何东西。另一方面，它每次只会回溯一层，因此可能会把大量时间浪费在一片必定会失败的搜索空间中。DPLL的运行思路如下：
- 回溯到首次赋值 → UNSAT
- 回溯到之前某次赋值
  - 撤销这次之后的所有赋值
  - 换一条没走过的路
冲突子句学习（CDCL算法）

CDCL的不同之处在于，我们是如何从这一步走入之前的冲突的信息，现在作为一个新的子句被加入到子句列表中，为要使这个新子句满足，我们一定不会再进入到之前的冲突了。它比DPLL多了一步操作，运行思路如下：
- 回溯到首次赋值 → UNSAT
- 回溯到之前某次赋值
  - 撤销这次之后的所有赋值
  - 这次冲突作为新的子句加入到条件中
  - 换一条没走过没冲突的路

在这里插入图片描述

2、Minisat求解器

官网：http://minisat.se/

Github：https://github.com/niklasso/minisat

Minisat的基本使用方法：https://blog.csdn.net/nbu_dahe/article/details/115518719

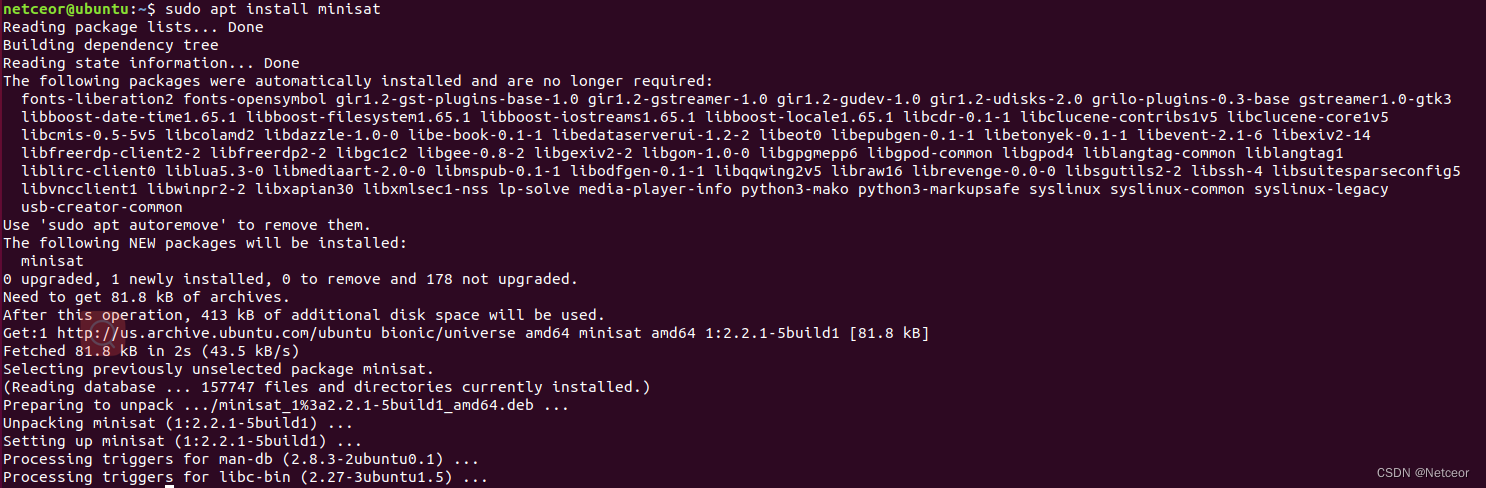
（1）安装

sudo apt install minisat

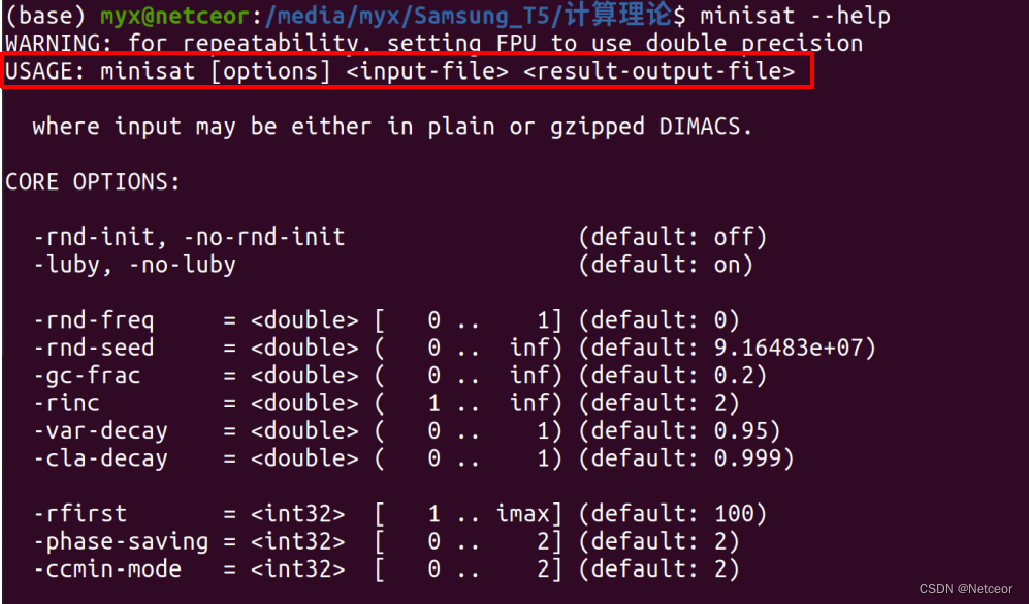
使用说明：minisat --help
- 使用格式：minisat [options] <input-file> <result-output-file>

（2）使用

创建CNF.txt文件如下，c代表注释行

【CNF.txt】
c An example DIMACS CNF
p cnf 2 3 
-1 2 0 
1 2 0
-1 -2 0

示例一

用minisat调用刚才创建的CNF.txt，结果输出到answer.txt

.txt的后缀名也可以改成.cnf

minisat CNF.txt answer.txt

运行完成后会在当前目录得到一个answer.txt

【answer.txt】
SAT
-1 2 0

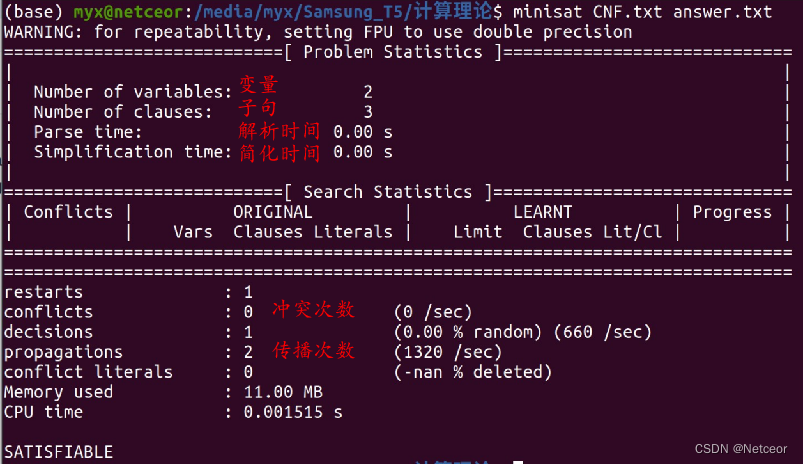
请添加图片描述

示例二

【CNF.txt】
p cnf 2 4
-1 2 0 
1 2 0
-1 -2 0
1 -2 0
【answer.txt】
UNSAT

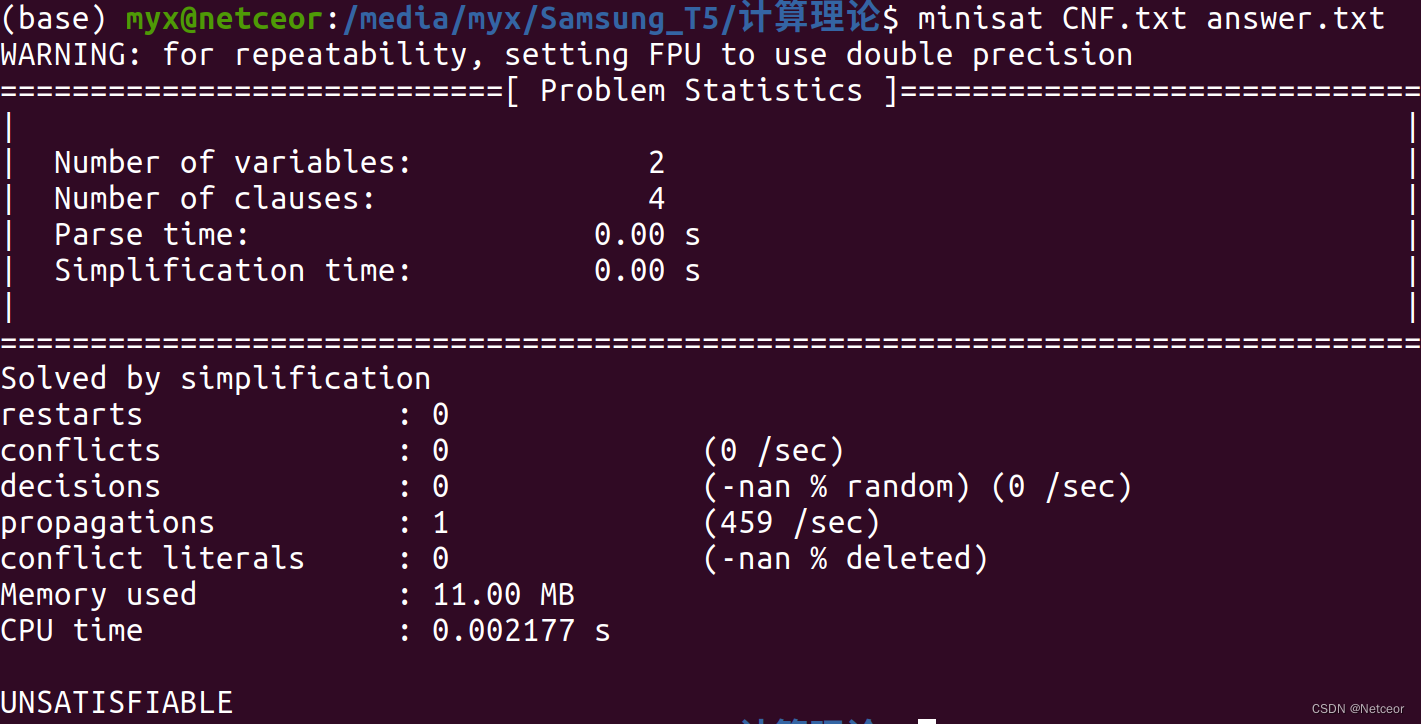
请添加图片描述

3、EasySAT求解器

Github： https://github.com/shaowei-cai-group/EasySAT

安装：在目录下make

4、其他求解器

CaDiCaL求解器：github

其他：GRASP、Chaff、SATO、BerkMin

二、SMT

1、介绍

这个SMT是在SAT的基础上实现的，目的是求出指定约束下的可行解。如果说SAT把注意力放在命题公式判定上，SMT就在SAT的基础上可以分析各种不等式和等式下的约束求解

SMT惰性算法流程如下：

1、对SMT公式进行预处理，把公式中的命题变量替换为布尔变量，再将SMT公式转化为可满足性意义上等价的SAT公式；
2、检查此SAT公式是否可满足，如果不可满足，那么SMT公式也不可满足，算法结束；
3、如果SAT公式可满足，则结合SMT背景理论去判断SMT公式的可满足性，返回判断结果，算法结束。
惰性算法是SAT求解器与对应的背景理论相结合的产物

2、z3-solver求解器

z3-solver是由Microsoft Research(微软)开发的SMT求解器，它用于检查逻辑表达式的可满足性，可以找到一组约束中的其中一个可行解，缺点是无法找出所有的可行解(对于规划求解问题可以是scipy) 。

z3-solver可应用于软/硬件的验证与测试、约束求解、混合系统的分析、安全、生物,以及几何求解等问题。

Z3主要由**C++**开发,提供了.NET、 C、 C++、 Java、 Python 等语言调用接口，下面以python接口展开讲解。

github：https://github.com/Z3Prover/z3

document：https://github.com/Z3Prover/z3/wiki/Documentation

API：C、C++、.NET、Java、Python、ML/OCaml
Z3 Guide
- z3介绍
- Python样例：Z3 API in Python（链接1）；Z3 API in Python（链接2）
- 网页端在线运行-Freeform Editing：应用SMTLIB语言
  - SMT-LIB语言介绍：https://zhuanlan.zhihu.com/p/624758007
Slide
Publications

（1）安装

pip install z3-solver importlib_resources

变量
- 整型(Int)，实型(Real)、向量(BitVec)和布尔(Bool)
  - Int(name)：创建一个整数变量，有名字
  - Ints(names)：创建多个整数变量，有名字
  - IntVal (val)：创建一个整数常量，有初始值
关键函数
- x, y = Ints(‘x y’) —设置变量
- s=solver() —创建解对象
  - s.add(条件)：为解增加一个约束
  - s.check()：检查解是否存在，存在则返回“SAT”
  - s.model()：返回解，即变量x和y的具体数值
  - s.assertions()：查看已经添加的约束And(a,b)、Or(a,b)、Not(a)、 Implies(a,b)

（2）使用-解数独问题

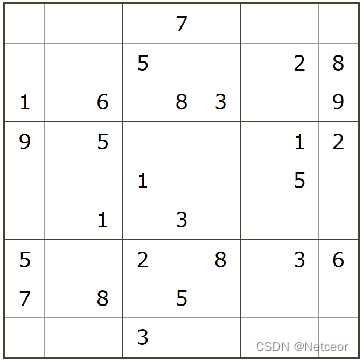
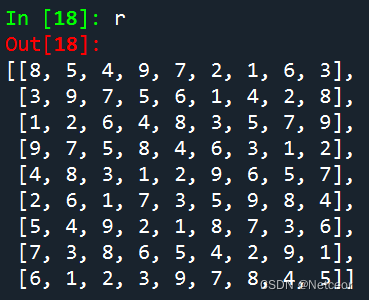
请添加图片描述

from z3 import *def solveShuDu(constraint, board: list):board_c = [If(board[i][j] == 0,True,X[i][j] == board[i][j])for i in range(9) for j in range(9)]s = Solver()s.add(constraint + board_c)if s.check() == sat:m = s.model()r = [[m[X[i][j]].as_long() for j in range(9)]for i in range(9)]return r# 1、变量：9x9 整数变量矩阵
X = [[Int(f"x_{i}_{j}") for j in range(9)] for i in range(9)]# 2、条件
# 每个单元格只能取1-9
cells_c = [And(1 <= X[i][j], X[i][j] <= 9) for i in range(9) for j in range(9)]# 每行每个数字最多出现一次
rows_c = [Distinct(X[i]) for i in range(9)]# 每列每个数字最多出现一次
cols_c = [Distinct([X[i][j] for i in range(9)]) for j in range(9)]# 每个 3x3 方格每个数字最多出现一次
sq_c = [Distinct([X[3*i0 + i][3*j0 + j]for i in range(3) for j in range(3)])for i0 in range(3) for j0 in range(3)]
# 数独完整约束条件
constraint = cells_c + rows_c + cols_c + sq_c# 3、求解
board = [[0, 0, 0, 0, 7, 0, 0, 0, 0],[0, 0, 0, 5, 0, 0, 0, 2, 8],[1, 0, 6, 0, 8, 3, 0, 0, 9],[9, 0, 5, 0, 0, 0, 0, 1, 2],[0, 0, 0, 1, 0, 0, 0, 5, 0],[0, 0, 1, 0, 3, 0, 0, 0, 0],[5, 0, 0, 2, 0, 8, 0, 3, 6],[7, 0, 8, 0, 5, 0, 0, 0, 0],[0, 0, 0, 3, 0, 0, 0, 0, 0]
]
r = solveShuDu(constraint, board)

参考样例：z3求解器(SMT)解各类方程各种逻辑题非常简单直观

3、Yices2求解器(Ubuntu)

（1）安装

官网： https://yices.csl.sri.com/index.html

安装

sudo add-apt-repository ppa:sri-csl/formal-methods
sudo apt-get update
sudo apt-get install yices2

（2）使用-解方程

使用格式：yices [option] <filename>
- 参考样例：https://yices.csl.sri.com/papers/manual.pdf（P34）

创建yices_example.txt

这是一个解方程问题，对于-y<0和y-10<0、-2x-7y<0

(define x::real)
(assert
(forall (y::real)
(=> (and (< (* -1 y) 0) (< (+ -10 y) 0))
(< (+ -7 (* -2 x) y) 0))))
(ef-solve)
(show-model)

运行 yices
```
yices --mode=ef yices_example.txt
```

4、CVC5求解器

（1）安装

官网： https://cvc5.github.io/
在线CVC： https://cvc5.github.io/app/
说明文档：https://cvc5.github.io/docs/cvc5-1.0.8/
安装

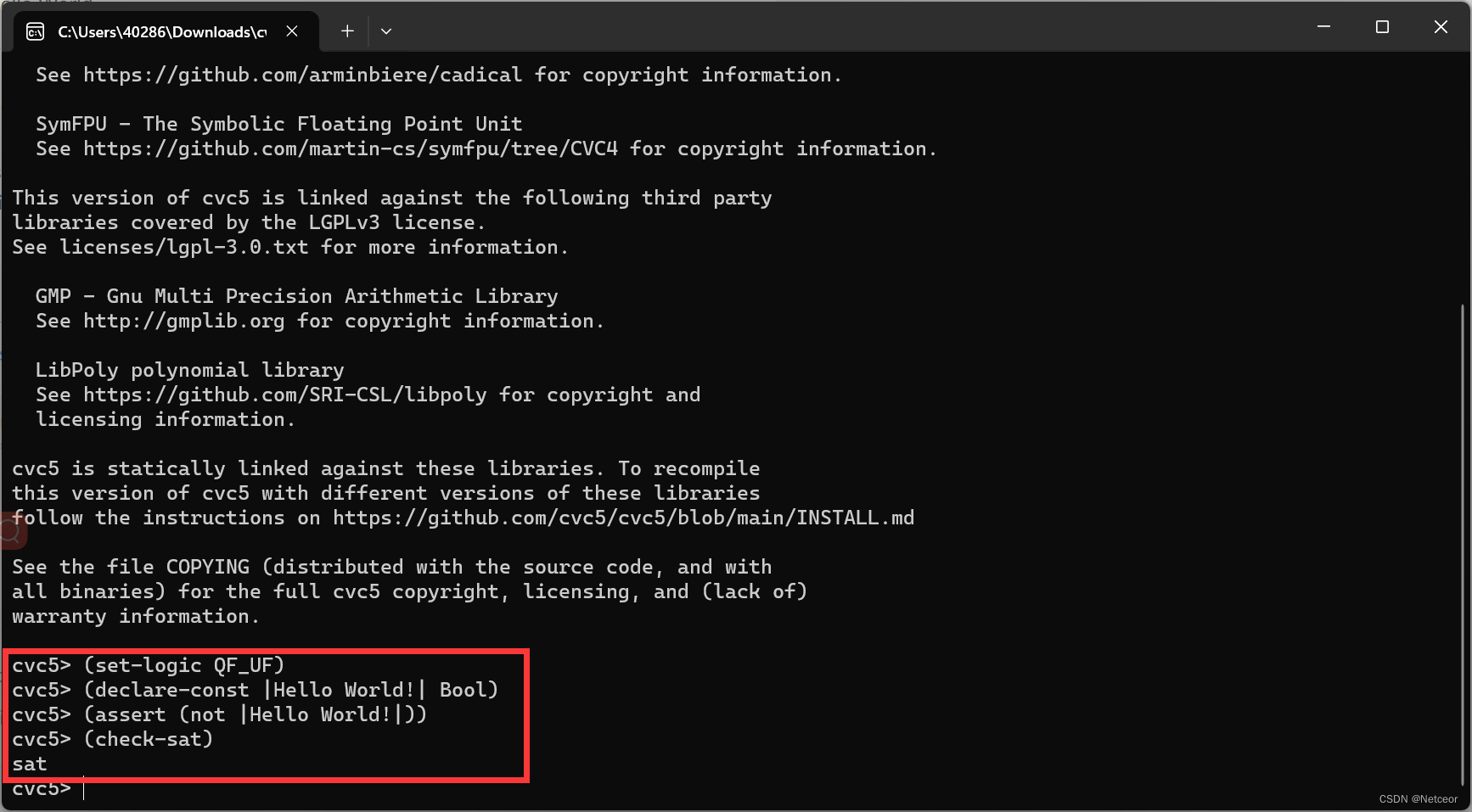
请添加图片描述

（2）使用-字符串判断

参考样例：
- https://cvc5.github.io/docs/cvc5-1.0.8/examples/examples.html
- https://smtlib.cs.uiowa.edu/examples.shtml (smtlib语言)
SMT-LIB语言：https://zhuanlan.zhihu.com/p/624758007

请添加图片描述