Tensorflow笔记（二）：常用函数2、激活函数、优化器等、神经网络模型实现（商品销量预测）-编程知识

Tensorflow笔记（二）：常用函数2、激活函数、优化器等、神经网络模型实现（商品销量预测）

import tensorflow as tf
import numpy as np
from tqdm import tqdm# ----------------------------- tensor常用函数2 -----------------------------------
a = tf.constant([1, 2, 3, 1, 2])
b = tf.constant([0, 1, 3, 4, 5])
c = tf.where(tf.greater(a, b), a, b)  # 若a>b，返回a对应位置的元素，否则返回b对应位置的元素rdm = np.random.RandomState(seed=110)  # 设置种子保证每次生成的随机数相同
a = rdm.rand()  # 返回一个随即标量
b = rdm.rand(2, 3)  # 返回维度为2行3列的随机数矩阵a2 = np.array([1, 2, 3])
b2 = np.array([4, 5, 6])
c2 = np.vstack((a2, b2))  # 将数组按垂直方向叠加x, y = np.mgrid[1:3:1, 2:4:0.5]  # 返回若干组维度相同的等差数组，格式为：起始值:结束值:步长
grid = np.c_[x.ravel(), y.ravel()]  # ravel函数将多维数组变为一维数组，c_则是使返回的间隔数值点配对y_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])  # 真实值（labels）
y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])  # 预测值（logits）
# 可以直接用交叉熵损失函数计算
loss_ce = tf.nn.softmax_cross_entropy_with_logits(y_, y)
# 也可以先用softmax把y_转换成概率，然后再求交叉熵损失
y_pro = tf.nn.softmax(y)
loss_ce = tf.losses.categorical_crossentropy(y_, y_pro)# ----------------------------- 商品销量神经网络预测模型 -----------------------------------
epochs = 15000
lr = 0.005
seed = 110
cost = 1  # 成本1元
profit = 99  # 利润99元rdm = np.random.RandomState(seed)
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10 - 0.05)] for (x1, x2) in x]  # 用公式生成销量（带噪声）
x = tf.cast(x, dtype=tf.float32)w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=seed))for epoch in tqdm(range(epochs)):with tf.GradientTape() as tape:y = tf.matmul(x, w1)# 如果销量预测多了（y>y_）则浪费成本了，如果销量预测少了（y<y_）则利润少了loss = tf.reduce_sum(tf.where(tf.greater(y, y_), cost * (y - y_), profit * (y_ - y)))grads = tape.gradient(loss, w1)w1.assign_sub(lr * grads)if epoch % 500 == 0:print(f"after {epoch} training steps, w1 is {w1.numpy()}")
# 因为利润更大，所以最后参数的结果会尽量给出大于1的系数

# ----------------------------- 神经网络复杂度 -----------------------------------

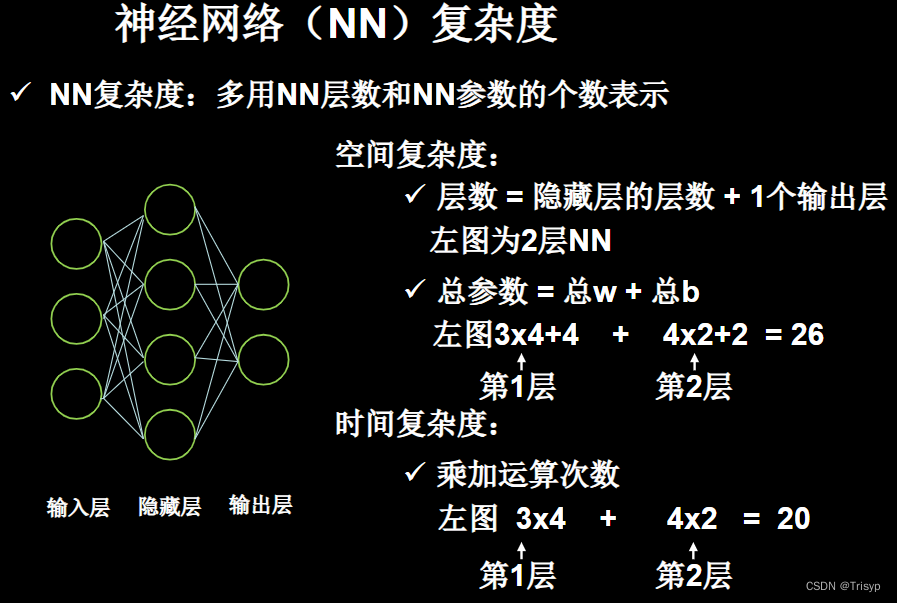
# ---------------------------------------------- 学习率 ----------------------------------------------------

# ---------------------------------------------- 激活函数 ----------------------------------------------------

优秀的激活函数:
非线性:激活函数非线性时，多层神经网络可逼近所有函数可微性:优化器大多用梯度下降更新参数
单调性:当激活函数是单调的，能保证单层网络的损失函数是凸函数
近似恒等性:f(x)≈x当参数初始化为随机小值时，神经网络更稳定
激活函数输出值的范围：
激活函数输出为有限值时，基于梯度的优化方法更稳定
激活函数输出为无限值时，建议调小学习率

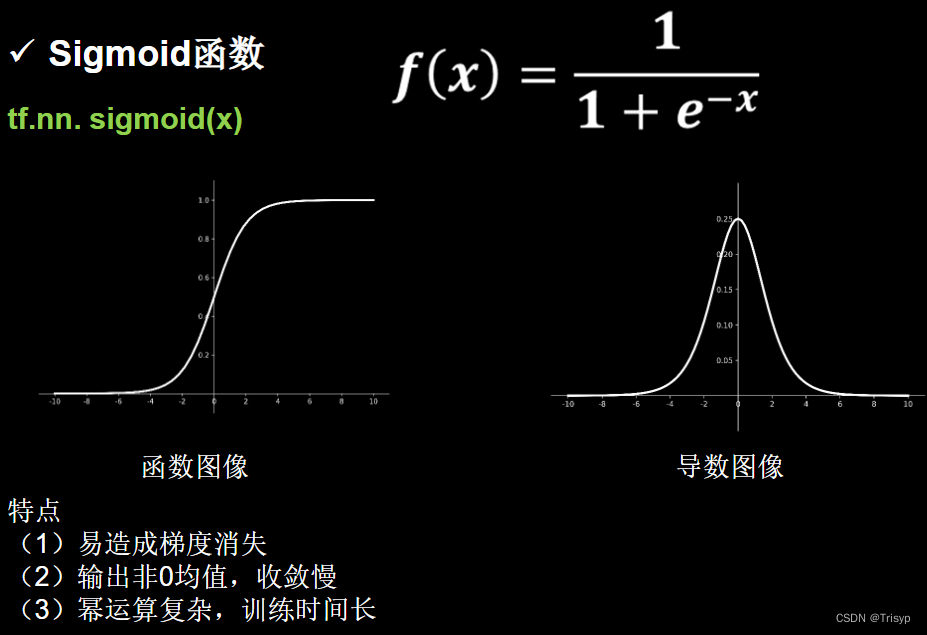
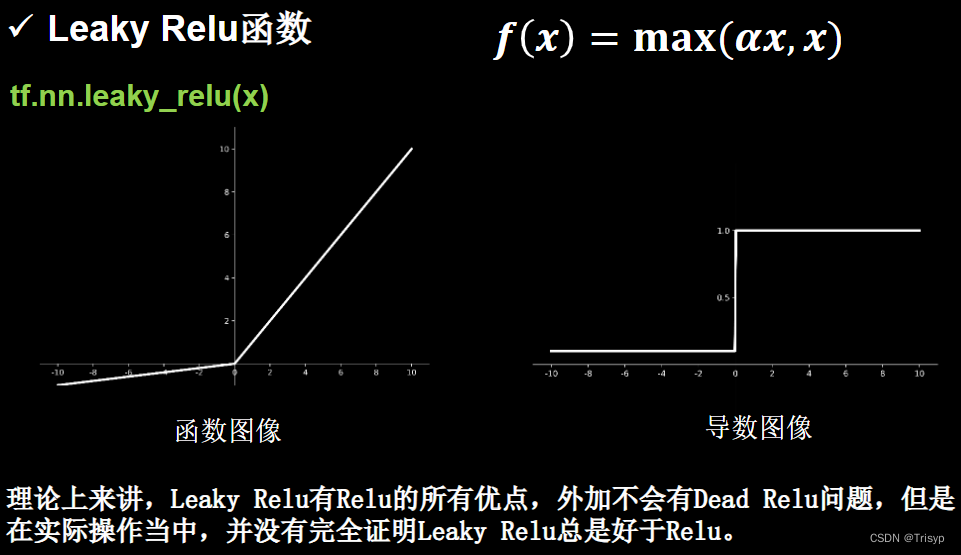
关于激活函数的选择，对于初学者的建议:
--首选relu激活函数:
--学习率设置较小值;
--输入特征标准化，即让输入特征满足以0为均值1为标准差的正态分布
--初始参数中心化，即让随机生成的参数满足以0为均值， $\sqrt{\tfrac{2}{feature-num}}$ 为标准差的正态分布，其中feature-num表示当前层输入特征个数。