引言

上一节介绍了线搜索方法使用非精确搜索近似求解最优步长的过程中，讨论了$f(x_{k+1})<f(x_k)$与 { f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk​)}k=0∞​⇒f∗之间的条件关系。本节以该条件关系为引，介绍$\text{Armijo Condition}$。

回顾：

关于$f(x_{k+1})=\varphi (\alpha )$的一些特性

在线搜索方法——步长角度(精确搜索)中介绍过，由于目标函数$f(\cdot )$未知，导致我们没有办法得到$\varphi (\alpha )=f(x_{k+1})$的精确函数，但并不妨碍我们了解一些关于$\varphi (\alpha )$的特性：

• 由于步长变量$\alpha$具有物理意义，因而$\alpha$存在下界$0$，从而$\varphi (0)=f(x_k+0\cdot {\mathcal{P}}_k)=f(x_k)$；
• $\varphi (\alpha )$在$\alpha =0$处的斜率$\begin{array}{r}\frac{\partial \varphi (\alpha )}{\partial \alpha }{|}_{\alpha =0}\end{array}$可表示成如下形式：
  $$\begin{array}{rl}\frac{\partial \varphi (\alpha )}{\partial \alpha }{|}_{\alpha =0}& ={\varphi }^{\prime }(0)\\ & ={\left[\nabla f(x_k+0\cdot {\mathcal{P}}_k)\right]}^T\cdot {\mathcal{P}}_k\\ & ={\left[\nabla f(x_k)\right]}^T\cdot {\mathcal{P}}_k\end{array}$$
  其中${\mathcal{P}}_k$是一个单位向量，描述的是下降方向；而$\nabla f(x_k)$表示梯度方向。因而它们的内积有：
  $$[\nabla f(x_k){]}^T\cdot {\mathcal{P}}_k<0$$

也就是说：无论$\varphi (\alpha )$是什么形式，该函数总会经过$[0,f(x_k)]$点，且该点处的斜率$<0$恒成立。最终，该点的切线函数$l(\alpha )$表示为：
$$l(\alpha )=f(x_k)+[\nabla f(x_k){]}^T{\mathcal{P}}_k\cdot \alpha$$

非精确搜索近似求解最优步长的条件

关于最优化目标函数$\underset{\mathcal{X}\in {\mathbb{R}}^n}{\min }f(\mathcal{X})$，使用线搜索方法获取一系列数值解 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk​}k=0∞​：
$$x_{k+1}=x_k+{\alpha }_k\cdot {\mathcal{P}}_k$$
最终目标希望：随着迭代过程的增加，$x_k$对应的目标函数结果$f(x_k)$收敛到最小值$f^{\ast }$：
{ f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk​)}k=0∞​⇒f∗
我们不否认：如果实现该目标，必然需要数值解序列对应的目标函数结果 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk​)}k=0∞​满足严格的单调性：

• 在最优解${\alpha }_k$没有求出之前，将步长视作一个变量$\alpha$。
• 观察$f(x_k+\alpha \cdot {\mathcal{P}}_k)$,由于$x_k,{\mathcal{P}}_k$都是已知/被固定的量，因此该式子中仅包含一个标量变量$\alpha$，以此将$f(x_{k+1})$视作仅关于$\alpha$的函数，记作$\varphi (\alpha )$。
  $$\{\begin{array}{l}\begin{array}{rl}& f(x_{k+1})=f(x_k+\alpha \cdot {\mathcal{P}}_k)=\varphi (\alpha )\\ & \varphi (\alpha )=f(x_{k+1})<f(x_k)=\varphi (0)\end{array}\end{array}$$

但如果 { f ( x k ) } k = 0 ∞ \{f(x_{k})\}_{k=0}^{\infty} {f(xk​)}k=0∞​仅仅满足严格的单调性，并无法证明 { f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk​)}k=0∞​⇒f∗。也就是说，这仅仅是一个必要不充分条件。
关于条件不充分的反例，见上一节传送门。

$\text{Armijo Condition}$

可以看出，条件$f(x_{k+1})<f(x_k)$的约束能力是松散的，因为该条件并没有考虑到目标函数$f(\cdot )$的复杂性。假设关于$\varphi (\alpha )$的函数图像表示如下(蓝色曲线)：

其中红色直线描述$f(x_{k+1})=\varphi (\alpha )=f(x_k)$的情况。如果按照条件$f(x_{k+1})<f(x_k)$的描述，那么红色线下方$\varphi (\alpha )$图像对应的$\alpha$结果均满足约束条件。

而$\text{Armijo Condition}$将$f(x_k)<f(x_{k+1})$这个条件之所以松散归结为：在$\varphi (\alpha )$函数中，满足$f(x_{k+1})<f(x_k)$条件下，可选择的步长$\alpha$结果过多，从而更不容易选择出最优步长。

基于这种动机，$\text{Armijo Condition}$的想法是：通过一种约束方法，基于该方法下有效降低步长$\alpha$的选择范围。那么如何构造这种方法$?$

• 回顾上图：关于初始点$\varphi (0)=f(x_k)$处的切线函数$l(\alpha )$(橙色线)。由于切线的原因，导致局部范围内，在该切线下方范围内找出一个有效的$\alpha$取值是极难的。
  这里主要关注的是‘凸函数’，在局部范围内如果是个凸函数，不可能在切线下方找到有效的$\alpha$值。
• 但这也仅限于局部范围内。如果在全局范围内，这种值还是有可能存在的。例如下面的$\varphi (\alpha )$图像：
  
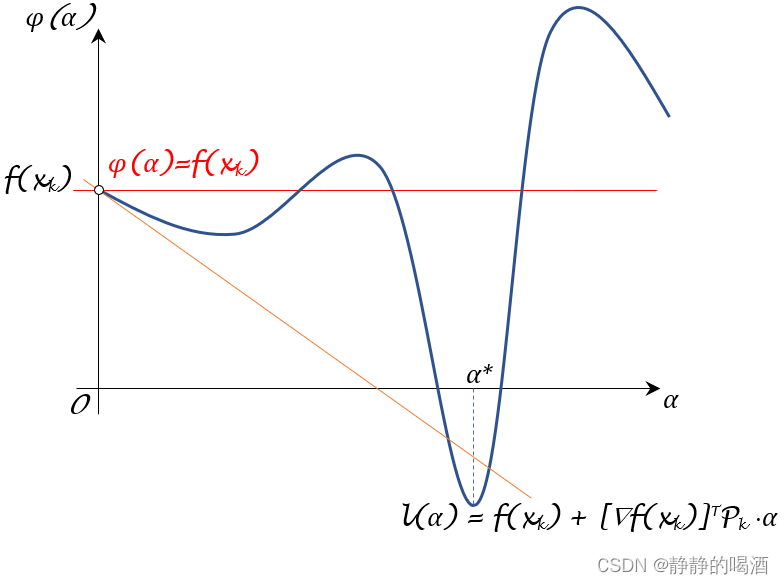
  从上图可以看出，关于过$[0,\varphi (0)]$的切线函数下方可能存在可选择的步长，并且从图像上观察，该步长范围的映射结果非常优秀。但实际上我们并不清楚$\varphi (\alpha )$的真实形状，但可以肯定的是：如果将$[0,\varphi (0)]$位置的切线作为约束条件，该切线筛选出的$\alpha$数量相比$f(x_{k+1})=f(x_k)$明显减少，甚至是苛刻的。
  上图仅是我们构想出的示例，实际上也可能会出现‘在切线$l(\alpha )$下方，没有任何$\varphi (\alpha )$图像的情况。这会使切线$l(\alpha )$自身作为约束条件返回的$\alpha$范围不稳定甚至是空集。因而我们需要选出一个位于$f(x_{k+1})=f(x_k)$与$l(\alpha )$之间的直线作为判别条件。
  $$\mathcal{L}(\alpha )=f(x_k)+{\mathcal{C}}_1\cdot \alpha [\nabla f(x_k){]}^T{\mathcal{P}}_k{\mathcal{C}}_1\in (0,1)$$
• 其中${\mathcal{C}}_1\in (0,1)$相当于以$f(x_k)$为中心，在$l(\alpha )$与$f(x_{k+1})=f(x_k)$所围成的范围内选择合适的斜率，从而得到相应的约束条件：
  • 由于$f(x_{k+1})=f(x_k)$自身斜率为$0$,因而$\mathcal{L}(\alpha )$斜率${\mathcal{C}}_1\cdot {\left[\nabla f(x_k)\right]}^T{\mathcal{P}}_k{\mathcal{C}}_1\in (0,1)$可看作是从 { 0 , [ ∇ f ( x k ) ] T P k } \{0, [\nabla f(x_k)]^T\mathcal P_k\} {0,[∇f(xk​)]TPk​}范围内滑动产生的斜率结果，并作为筛选$\alpha$的约束条件。
  • 关于新的约束条件见绿色线,可以看出，可以通过调节参数${\mathcal{C}}_1$,从而约束$\alpha$的可选择范围。
    
    从上图可以看出：
• 关于新的约束函数$\mathcal{L}(\alpha )$，其斜率${\mathcal{C}}_1\cdot {\left[\nabla f(x_k)\right]}^T$的上界是$0$，对应$\mathcal{L}(\alpha )=f(x_k)$；
• 对应地，其斜率${\mathcal{C}}_1\cdot {\left[\nabla f(x_k)\right]}^T{\mathcal{P}}_k$的下界是${\left[\nabla f(x_k)\right]}^T{\mathcal{P}}_k$，对应$\mathcal{L}(\alpha )=l(\alpha )$；

从而将$\varphi (\alpha )\le f(x_k)+{\mathcal{C}}_1\cdot {\left[\nabla f(x_k)\right]}^T{\mathcal{P}}_k\cdot \alpha$称作$\text{Armijo Condition}$。

相关参考：
【优化算法】线搜索方法-步长-Armijo Condition