算法空间复杂度计算-编程知识

空间复杂度定义

影响空间复杂度的因素

算法在运行过程中临时占用的存储空间讲解

例子

斐波那契数列递归算法的性能分析

二分法（递归实现）的性能分析

空间复杂度定义

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。
一个算法在计算机存储器上所占用的存储空间，包括程序代码所占用的空间，输入数据所占用的空间和辅助变量所占用的空间这三个方面。

影响空间复杂度的因素

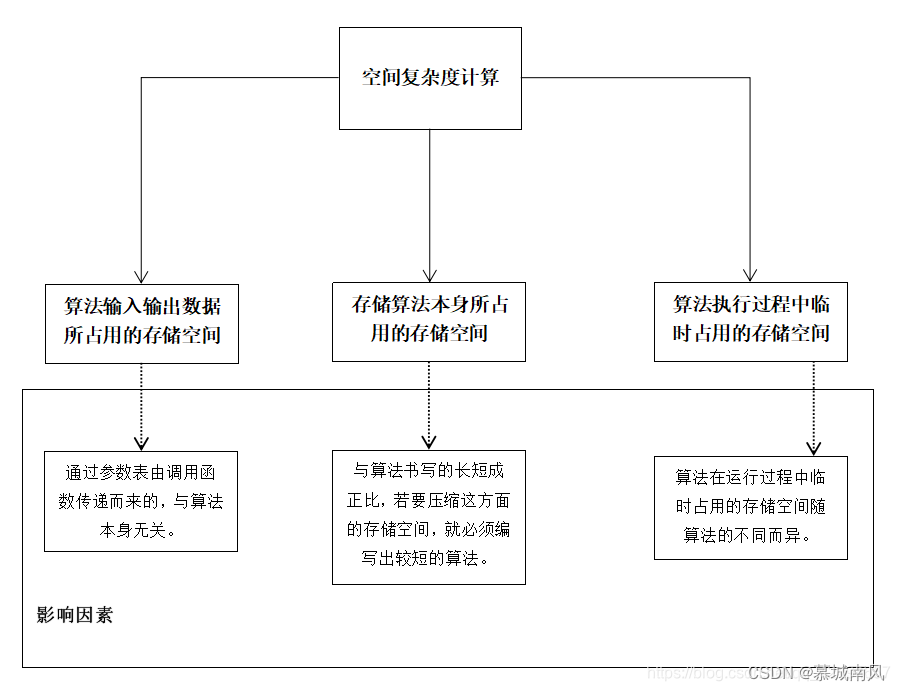
注意：
一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小，它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。若一个算法为递归算法，其空间复杂度为递归所使用的堆栈空间的大小。它等于一次调用所分配的临时存储空间的大小乘以被调用的次数(即为递归调用的次数加1，这个1表示开始进行的一次非递归调用)
递归的空间复杂度：每次递归所开空间*深度。

算法在运行过程中临时占用的存储空间讲解

1、有的算法只需要占用少量的临时工作单元，而且不随问题规模的大小而改变，我们称这种算法是“就地”进行的，是节省存储的算法，下面会介绍。

2、有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况。

计算方法
①忽略常数，用O(1)表示
②递归算法的空间复杂度=递归深度n*每次递归所要的辅助空间
③对于单线程来说，递归有运行时堆栈，求的是递归最深的那一次压栈所耗费的空间的个数，因为递归最深的那一次所耗费的空间足以容纳它所有递归过程。

为什么要求递归的深度呢？

因为每次递归所需的空间都被压到调用栈里（这是内存管理里面的数据结构，和算法里的栈原理是一样的），一次递归结束，这个栈就是就是把本次递归的数据弹出去。所以这个栈最大的长度就是递归的深度。

例子

1、空间算法的常数阶

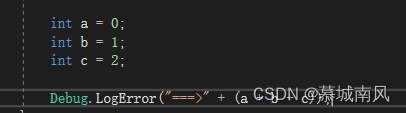
如上图，这里有三个局部变量分配了存储空间，所以f(n) = 1 + 1 + 1 = 3，根据上面的法则该函数不受n的影响且为常数项，所以空间复杂度记作O(1)。这种与问题的大小无关（n的多少），执行时间恒定的算法，我们称之为具有O(1)的空间复杂度，又叫常数阶。

2、两个函数，空间复杂度分别为 $O(1), O(n)$ ：

# O(1)
def f1(n):j = 0for i in range(n):j += 1return j# O(n)
def f2(n):a = []for i in range(n):a.append(i)return a

在第一个函数中，所需开辟的内存空间并不会随着n的变化而变化，即此算法空间复杂度为一个常量，所以表示为O(1)。在第二个函数中，随着n的增大，开辟的内存大小呈线性增长，这样的算法空间复杂度为O(n)。在递归的时候，会出现空间复杂度为logn的情况，比较特殊。

3、空间算法的线性阶（递归算法）

如上图，这是一个递归算法（计算从n + (n-1) + (n-2) + … + 2 + 1的和）
每当执行一次该函数就会为tmp分配一个临时存储空间，所以f(n) = 1*(n-1+1) = n，函数是受n影响的所以空间复杂度记为O(n)

斐波那契数列递归算法的性能分析

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……
这个数列从第3项开始，每一项都等于前两项之和。

如果设F(n）为该数列的第n项（n∈N*），那么这句话可以写成如下形式：:F(n)=F(n-1)+F(n-2)

显然这是一个线性的递推数列。

通项公式：

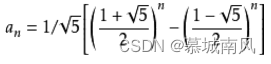
上面就是斐波那契数列的递推公式，这样一个完全是自然数的数列，通项公式却是用无理数来表达的。而且当n趋向于无穷大时，前一项与后一项的比值越来越逼近黄金分割0.618

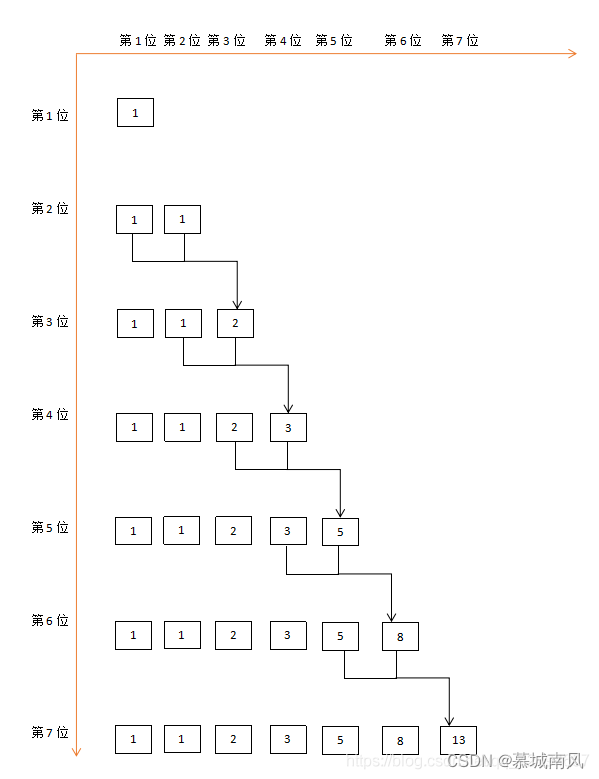
递推是公式是求解斐波那契数列的一个方法，我们当然也可以用计算机编写程序来求解。

方法一（迭代法）

  /// <summary>/// 斐波那契（迭代法）/// </summary>/// <param name="n"></param>/// <returns></returns>int Fibonacci(int n){if (n <= 0)return -1;if (n == 1 || n == 2)return 1;else{int num = 0;int a = 1;int b = 1;while (n - 2 > 0){num = a + b;a = b;b = num;n--;}return num;}}

时间复杂度：
while以外的算法语句都忽略不计(不随n的变化而变化)
while算法语句所有语句
f(n) = 4 *（n - 2） = 4n - 8
时间复杂度记为:O(n)

空间复杂度：
算法中num、a、b只创建1次
s(n) = 1 + 1 + 1 = 3
空间复杂度记为:O(1)

方法二（递归法）

def fibonacci(n):if n <= 0:return 0elif n == 1:return 1else:return fibonacci(n - 1) + fibonacci(n - 2)

首先回顾一下时间复杂度：递归算法的时间复杂度 = 递归的次数 * 每次递归中的操作次数。每次递归进行了一次加法操作，时间复杂度是O(1)，递归的次数可以抽象成一棵递归树：（以n=5为例）

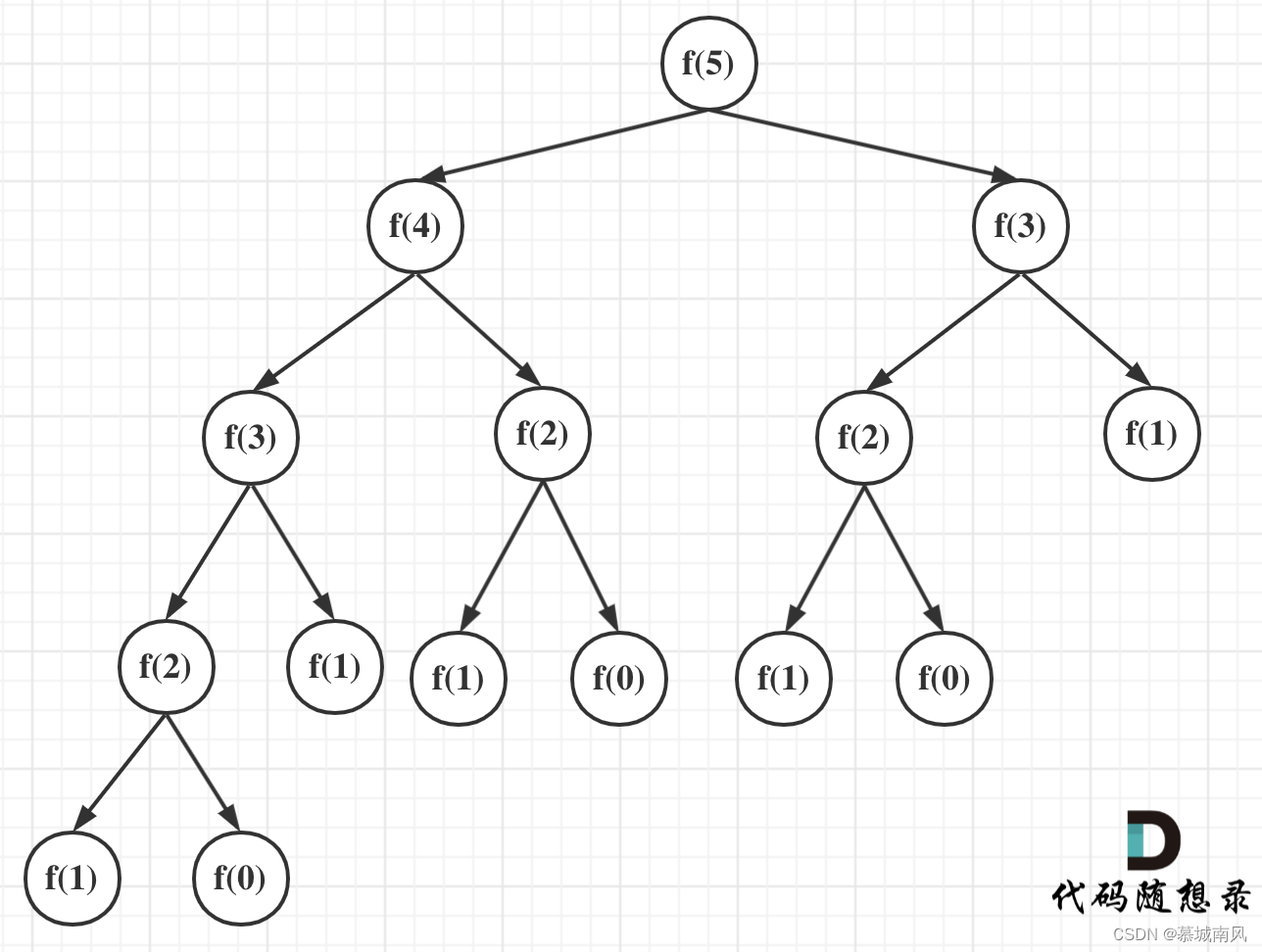
在这棵二叉树中每一个节点都是一次递归，一棵深度（按根节点深度为1）为k的二叉树最多可以有个节点，所以该递归算法的时间复杂度为O(2^n)，这个复杂度是非常大的，随着n的增大，耗时是指数上升的。

然后再来看空间复杂度：递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度。

为什么要求递归的深度呢？因为每次递归所需的空间都被压到调用栈里（这是内存管理里面的数据结构，和算法里的栈原理是一样的），一次递归结束，这个栈就是把本次递归的数据弹出去。所以这个栈最大的长度就是递归的深度。

回到斐波那契数列的例子，每次递归所需要的空间大小都是一样的，所以每次递归中需要的空间是一个常量，并不会随着n的变化而变化，每次递归的空间复杂度就是 O(1)。递归的深度如图所示：

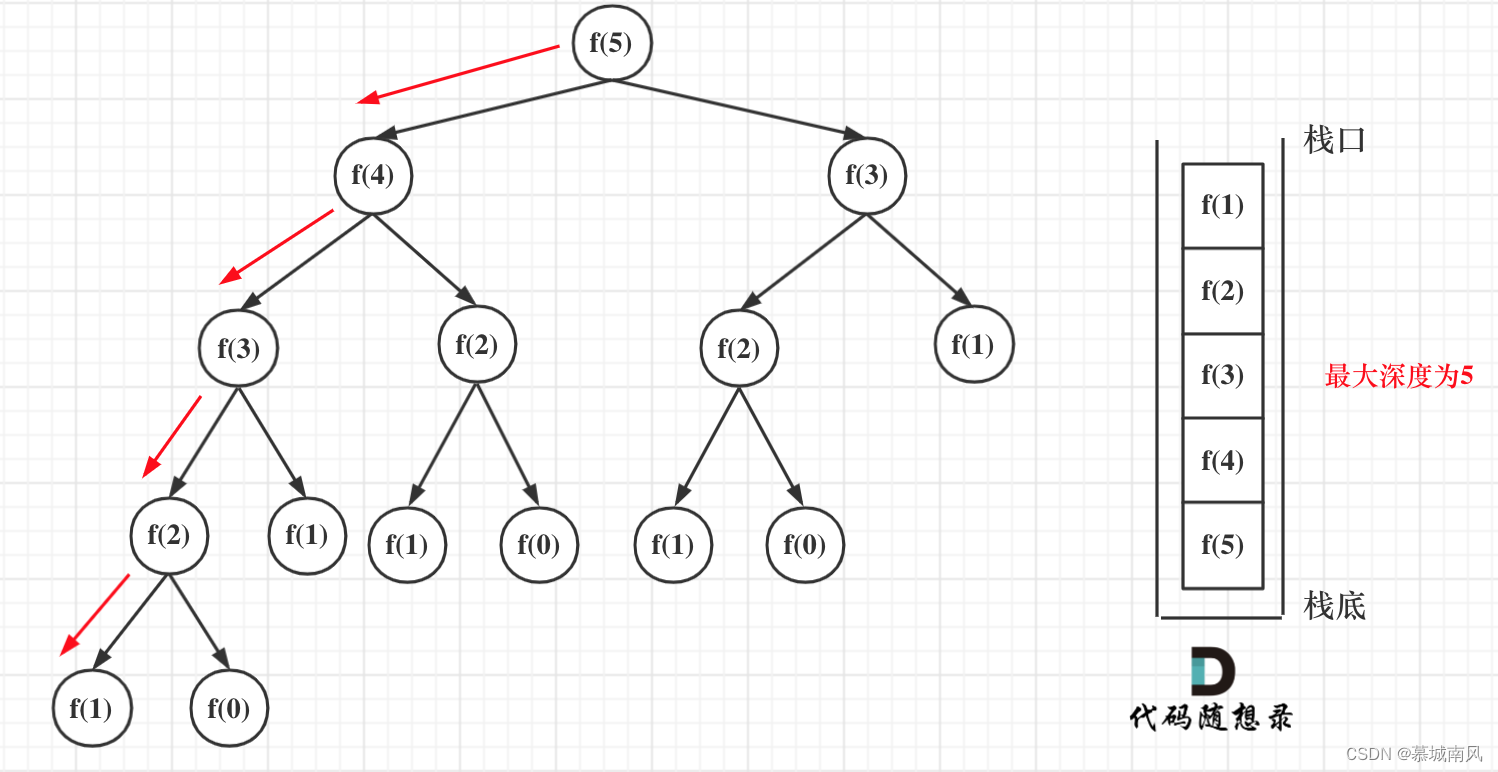
递归第n个斐波那契数的话，递归调用栈的深度就是n。那么每次递归的空间复杂度是O(1)，调用栈深度为n，所以这段递归代码的空间复杂度就是O(n)。

此算法时间复杂度非常高的主要原因是最后一行的两次递归，所以优化算法的方向就是减少递归的调用次数：

def fibonacci(first, second, n): #初始值 first = second = 1if n <= 0:return 0elif n <= 2:return 1elif n == 3:return first + secondelse:return fibonacci(second, first + second, n - 1)

举例来说 n=5 时 fibonacci(1,1,5) → fibonacci(1,2,4) → fibonacci(2,3,3) → 2+3=5。这里相当于用first和second来记录当前相加的两个数值，此时就不用两次递归了。因为每次递归的时候n减1，即只是递归了n次，所以时间复杂度是 O(n)。同理递归的深度是n-2，每次递归所需的空间还是常数，所以空间复杂度依然是O(n)。

最后总结一下：

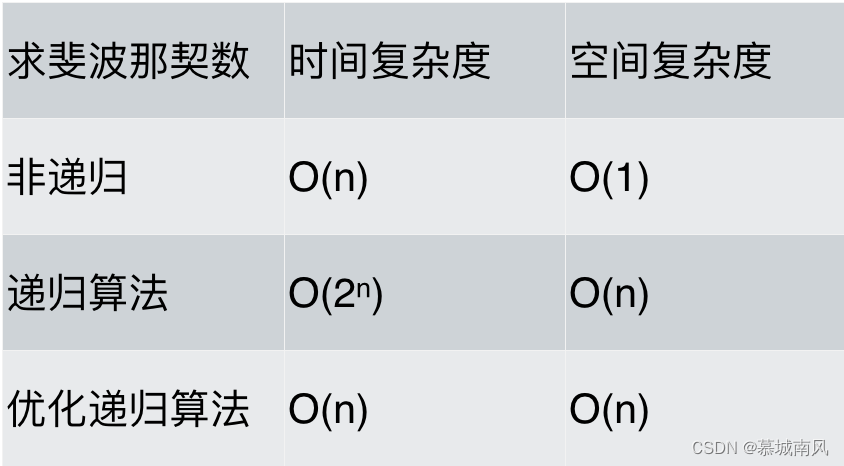
可以看出，求斐波那契数的时候，使用递归算法并不一定在性能上是最优的，但递归确实简化了代码层面的复杂度。

二分法（递归实现）的性能分析

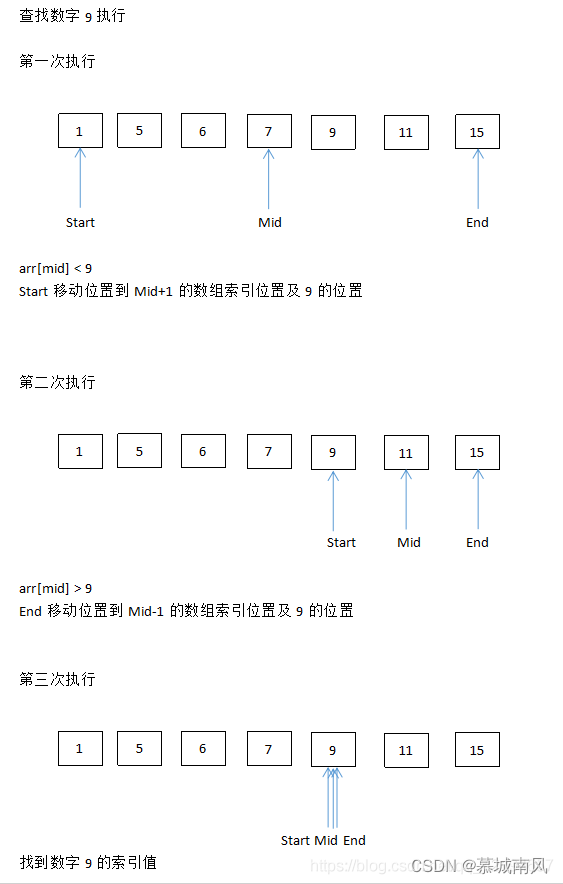
方法一（迭代法）

	/// <summary>/// 二分查找/// </summary>/// <param name="arr">查找数组</param>/// <param name="len">数组长度</param>/// <param name="num">查找项</param>/// <returns></returns>int BinarySearch(int[] arr,int len,int num){int left = 0;int right = len - 1;int mid;while (left <= right){mid = (left + right) / 2;if (arr[mid] > num)right = mid - 1;else if (arr[mid] < num)left = mid + 1;elsereturn mid;}return -1;}

时间复杂度：
left、right、mid运算次数
f(n1) = 1 + 1 + 1 = 3
我们将While循环中的运算作为一个整体看待，每次都是折半运算次数
f(n2) = log2^n
总运行次数
f(all) = f(n1)+f(n2) = 3 + log2 ^ n
时间复杂度记为:O(log2^n)

空间复杂度：
算法中left、right、mid只创建的次数
s(n) = 1 + 1 + 1 = 3
空间复杂度记为:O(1)

方法二（递归法）

def binary_search(arr, l, r, x):if r >= l:mid = l + (r - l) // 2if arr[mid] == x:return midelif arr[mid] > x:return binary_search(arr, l, mid - 1, x)else:return binary_search(arr, mid + 1, r, x)else:return -1

此算法时间复杂度为O(logn)。每次递归的空间复杂度主要就是参数里传入的这个arr数组，但需要注意的是在C/C++中函数传递数组参数，不是整个数组拷贝一份传入函数而是传入数组首元素地址。也就是说每一层递归都是公用一块数组地址空间的，所以每次递归的空间复杂度是常数即：O(1)。（Python呢？）再来看递归的深度，二分查找的递归深度是logn ，递归深度就是调用栈的长度，那么这段代码的空间复杂度为 1 * logn = O(logn)。

注意：关注语言在传递函数参数时，是拷贝整个数值还是拷贝地址，如果是拷贝整个数值那么该二分法的空间复杂度就是O(nlogn)。