pytorch（十）循环神经网络-编程知识

文章目录

- 卷积神经网络与循环神经网络的区别
- RNN cell结构
- 构造RNN
- 例子 seq2seq

卷积神经网络与循环神经网络的区别

卷积神经网络：在卷积神经网络中，全连接层的参数占比是最多的。

卷积神经网络主要用语处理图像、语音等空间数据，它的特点是局部连接和权值共享，减少了参数的数量。CNN通常包括卷积层、池化层和全连接层，卷积层用于提取输入数据的特诊，池化层用语降维和压缩特征，全连接层将特征映射到更加高维度的空间中。

卷积神经网络在处理空间数据的时候，其输入通常是一个二维或者三维的张量，每一个元素对应一个输出。CNN通过卷积操作获取特征，这些特征往往是局部相关的，即每个特征都与输入数据的一个局部区域相关联（相邻的特征往往具有相似性）。

循环神经网络

循环神经网络主要用于处理序列数据，比如自然语言处理、语音识别和时间序列预测（具有时间依赖的数据），它的特点是具有时间轴，能够保留和处理序列中的历史信息。RNN包括循环层，能够接收前一层的信息并且与当前的输入结合，生成当前的输出序列。

循环神经网络处理的数据往往是序列数据，即输入的数据是一个序列，每一个时间步都有一个对应的输出，RNN通过循环层保留和传递历史信息，从而建立时间上的依赖关系。

循环神经网络也使用到了权值共享的想法，RNN在不同的时间位置共享参数（CNN在不同的空间位置共享参数）

RNN cell结构

RNN cell的结构在本质上类似于传统的神经网络模型（输入层、隐藏层、输出层），但是RNN于传统的NN最大的区别在于：隐藏层的输入不仅包括输入层的输出，还包括上一时刻隐藏层的输出，其结构如下：

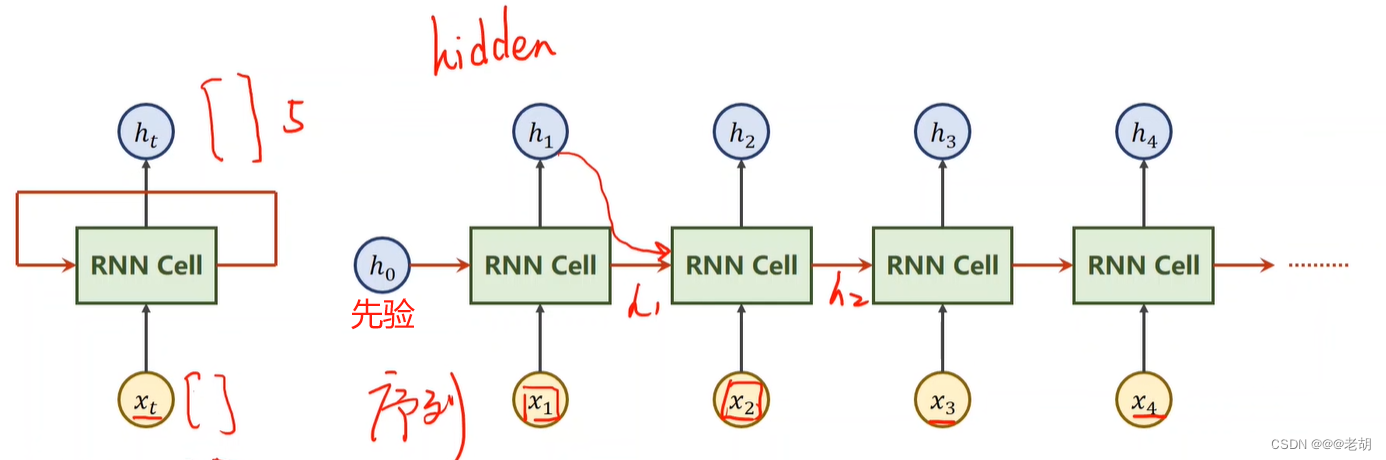
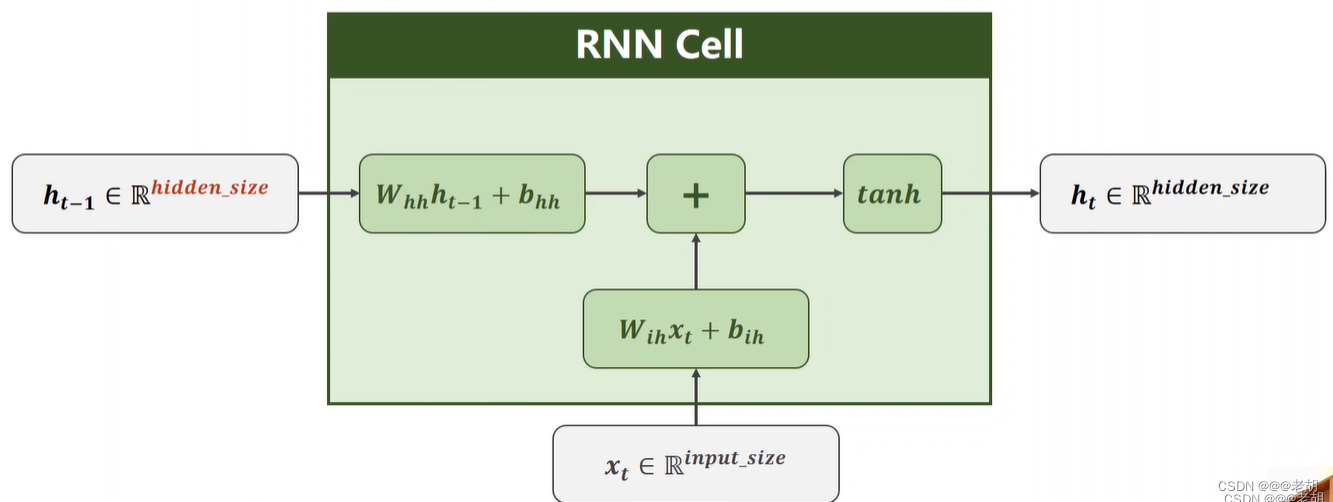
在这里插入图片描述

之所以叫做循环神经网络，是因为以上的cell都是同一个cell，参数也只有cell里的一份而已，在训练中，cell层使用的是循环结构，使用不同的输入数据进行训练。

构造RNN

第一种方法 RNNCell

cell=torch.nn.RNNCell(input_size=input_size,hidden_size=hidden_size)
hidden=cell(input,hidden)
# input of shape(batch,input_size)
# hidden of shape(batch,hidden_size)
# output of shape(batch,hidden_size)
# dataset.shape(seqLen,batchSize,inputSize)

import torchbatch_size=1 # N=1
seq_len=3 # x=[x1,x2,x3]
input_size=4 # [4*3]
hidden_size=2 # [2*3]
# 两种构造方式——1
cell=torch.nn.RNNCell(input_size=input_size,hidden_size=hidden_size)#(seq,batch=n,features) 序列的长度 * 批量 * 维度
dataset=torch.randn(seq_len,batch_size,input_size)
# 批量 * 维度
hidden=torch.zeros(batch_size,hidden_size)print('dataset:',dataset)
print('hidden:',hidden)# 构造循环
for idx,input in enumerate(dataset):print('=' *20,idx,'='*20)print(input)print('Input size:',input.shape)hidden=cell(input,hidden)print(hidden)print('Outputs size:',hidden.shape)print(hidden)

第二种方法

cell=torch.nn.RNN(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers)
out,hidden=cell(input,hidden)
# input：表示整个输入序列；input of shape(seqSize,batch,input_size),这里的seqSize实际上就是上面的循环过程
# hidden：表示h0；hidden of shape(numLayers,batch,hidden_size)
# output of shape(seqLen,batch,hidden_size)

import torchbatch_size=1 # N=1
seq_len=3 # x=[x1,x2,x3]
input_size=4 # [4*3]
hidden_size=2 # [2*3]
num_layers=1
# 两种构造方式——2 num_layers表示层数
cell=torch.nn.RNN(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers)
# cell=torch.nn.RNN(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers)
# inputs=torch.randn(batch_size,seq_len,input_size)inputs=torch.randn(seq_len,batch_size,input_size)
hidden=torch.zeros(num_layers,batch_size,hidden_size)out,hidden=cell(inputs,hidden)
print('Output size:',out.shape)
print('Output:',out)
print('Hidden size:',hidden.shape)
print('Hidden:',hidden)

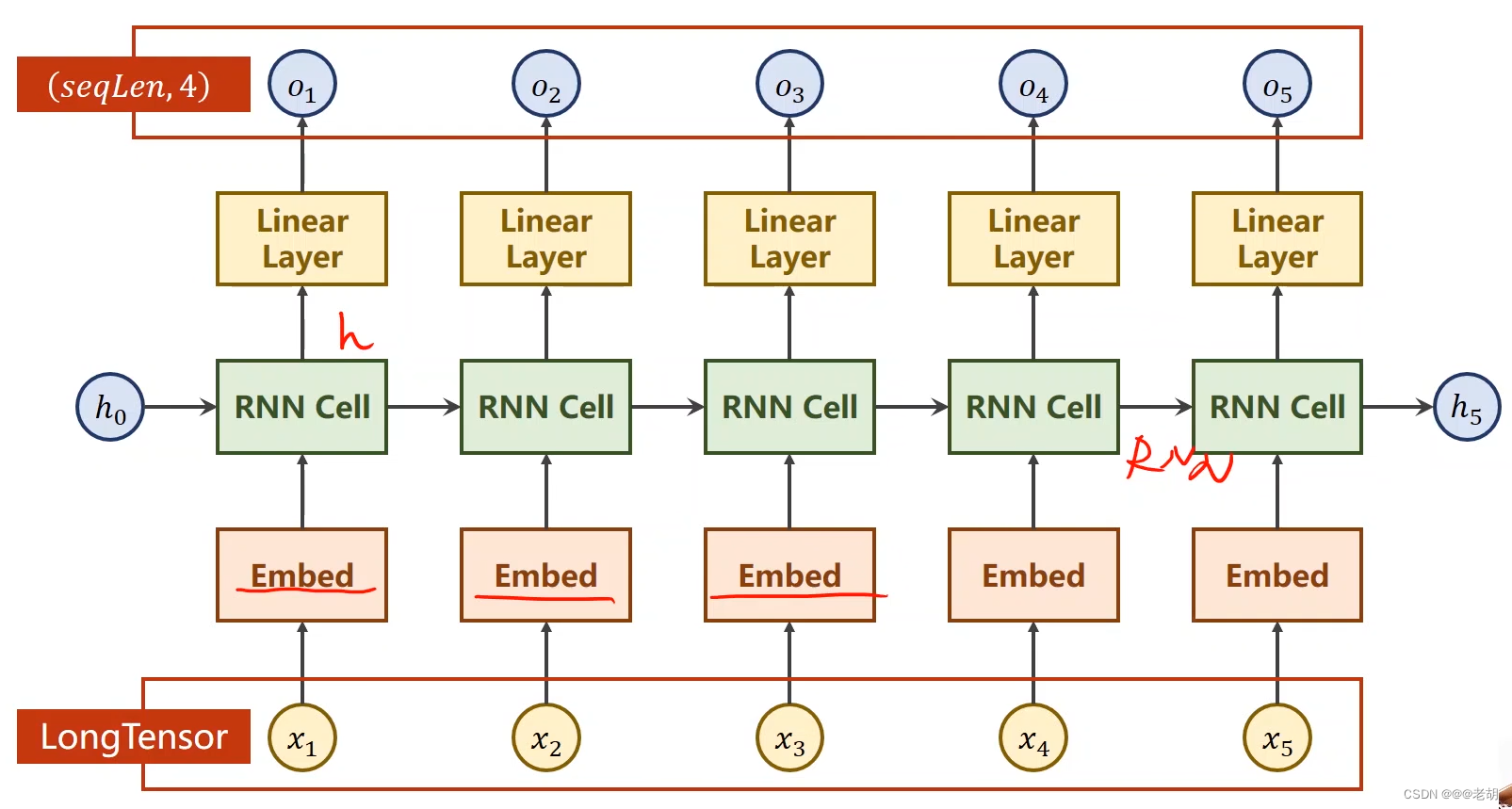
例子 seq2seq

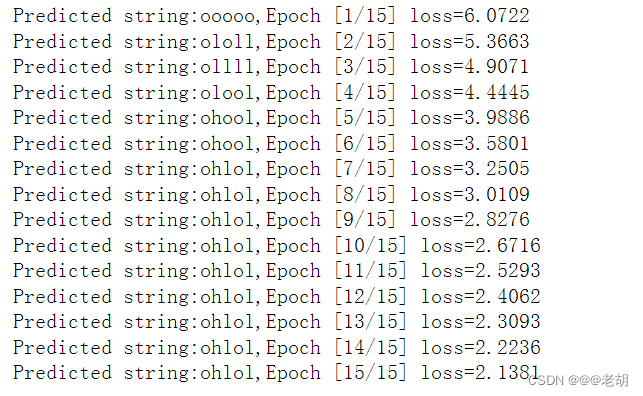
需要把 hello 序列经过训练变成 ohlol 序列，x=[x1,x2,x3,x4,x5]

这里是需要训练一个模型，使得输入“hello”，而输出为“ohlol”，实际上对于输入的数据，判别输出的数据属于哪一个类别，这里只有4种字母，所以输出的维度为4。

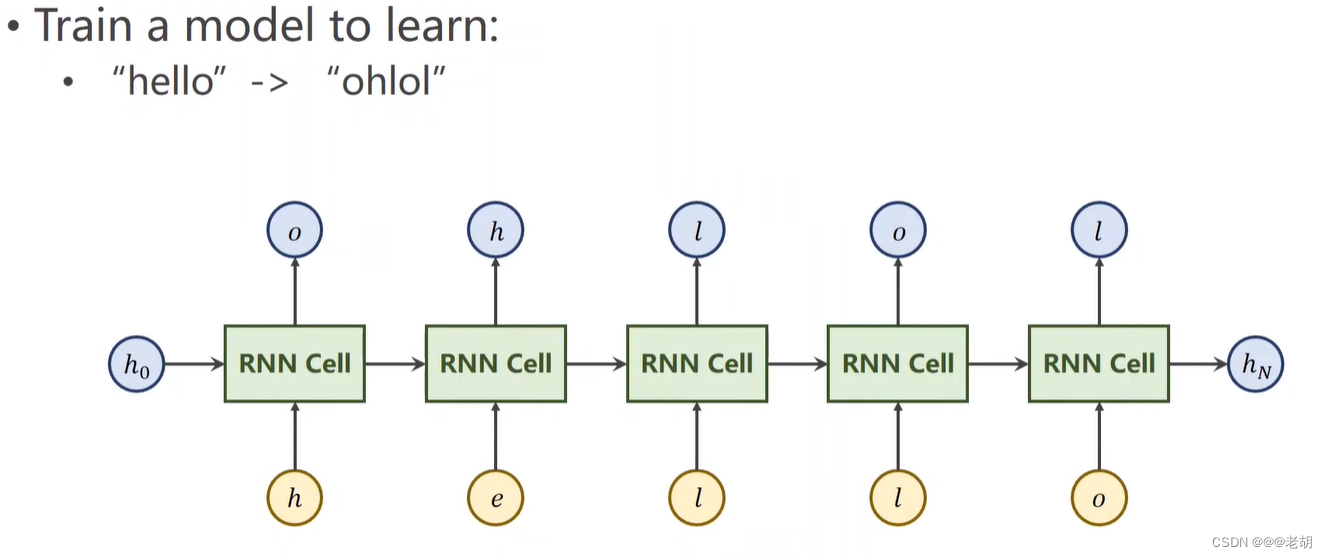
在这里插入图片描述

将序列数据转变成向量，一般转换为独热向量

在这里插入图片描述

import torchbatch_size=1
input_size=4
hidden_size=4idx2char=['e','h','l','o']
# 字典转变
x_data=[1,0,2,2,3]
y_data=[3,1,2,3,2]one_hot_looup=[[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]]x_one_hot=[one_hot_looup[x] for x in x_data]# 两个数据中的-1表示序列的长度seqSize
inputs=torch.Tensor(x_one_hot).view(-1,batch_size,input_size)
print('inputs:',inputs)
labels=torch.LongTensor(y_data).view(-1,1)class Model(torch.nn.Module):def __init__(self,input_size,hidden_size,batch_size):super(Model,self).__init__()self.batch_size=batch_sizeself.input_size=input_sizeself.hidden_size=hidden_sizeself.rnncell=torch.nn.RNNCell(input_size=self.input_size,hidden_size=self.hidden_size)def forward(self,input,hidden):hidden=self.rnncell(input,hidden)return hidden# h0def init_hidden(self):return torch.zeros(self.batch_size,self.hidden_size)net=Model(input_size,hidden_size,batch_size)
criterion=torch.nn.CrossEntropyLoss()
optimizer=torch.optim.Adam(net.parameters(),lr=0.1)for epoch in range(15):loss=0optimizer.zero_grad()hidden=net.init_hidden()print('Predicted string:',end='')# 这个实际上就是RNNfor input,label in zip(inputs,labels):# print('input:',input,'label:',label)hidden=net(input,hidden)loss+=criterion(hidden,label)# 输出可能性最大的那个值，也就是预测的值_,idx=hidden.max(dim=1)print(idx2char[idx.item()],end='')loss.backward()optimizer.step()print(',Epoch [%d/15] loss=%.4f'%(epoch+1,loss.item()))