题意翻译
对于下图中的树,
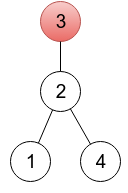
可以用数组表示为 [2,3,3,2]。这种可以表示树的数组(即有效)需要符合以下条件:
- 有且只有一个索引 r ,符合pr=r 。其中顶点 r 是树的根。
- 对于所有剩下的 n−1 个顶点 i 一定要有在 i 和 pi 之间的边。
比如 数列 (1,2,2)、(2,3,1) 和 (2,1,3) 都是因为根的数目而导致不有效。
现在给你一个数组 a1,a2,⋯,an,不一定是有效的。你需要对数组里面的值,通过最小次数的更改,使得这个数组有效。
并输出最小更改次数和一个通过最小更改次数而更改成功的有效数组。
如果有多种解,只需说出任何一组。
输入格式
第一行是一个整数 n (2≤n≤200000) ----树的顶点个数。
第二行包含 n 个整数 (1≤ai≤n。
输出格式
第一行一个整数,最小更改次数。
第二行输出任意一个通过最小更改次数而更改成功的有效数组。
说明
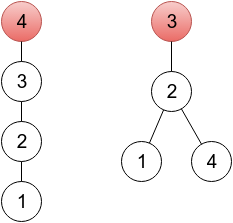
- 第一个样例只需要改一个就好啦!第一个样例输出是一个扎根于顶点 44 的树(因为 p4=4),你可以在下面的图中看到。另一个正确的答案应该是数列 2,3,3,2,扎根在顶点 3,也可以在下面的图中看到。两个图中顶点将用红色标出。
- 第二个样例中,给出的数列已经是有效的了。
输入输出样例
输入 #1复制
4 2 3 3 4
输出 #1复制
1 2 3 4 4
输入 #2复制
5 3 2 2 5 3
输出 #2复制
0 3 2 2 5 3
输入 #3复制
8 2 3 5 4 1 6 6 7
输出 #3复制
2 2 3 7 8 1 6 6 7
说明/提示
In the first sample, it's enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex 4 (because p4=4 ), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex 3 (right drawing below). On both drawings, roots are painted red.
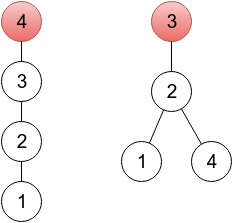
In the second sample, the given sequence is already valid.
解析:
本题的题意:
给定一些连接的点,可以时有环的,也可以是没有环的。将他们全部合成一颗树,树根只有一个。
我们考虑,确定一个为树根,将自环的一个节点,连接到给定的根节点上,这样子就解环了。
修改的次数可以复制一个数组和原数组做对比。
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;long long n,a[2000010],f[2000010],vis[2000010],root =0,tot=0,ans;void dfs(long long u){if(vis[u]) return;vis[u]=tot;if(f[u]==u){if(!root) root=u;//如果本来没有root它自己就当rootelse{f[u]=root;}return;} if(vis[f[u]]){if(vis[f[u]]==tot){//是环if(!root){f[u]=u;// 把u设为根root=f[u];}else{f[u]=root; //当前点连接到 设定的根节点 } }return;}dfs(f[u]);
}int main(){long long i,j,u,v;cin>>n;for(i=1;i<=n;i++){cin>>a[i];}memcpy(f,a,sizeof(a));for(i=1;i<=n;i++){//提前找rootif(f[i]==i){root=i;break;}}for(i=1;i<=n;i++){tot++;//这是一个细节坑点:有可能你之前访问过树的一部分(不是环),所以每次dfs都要打不同的标记dfs(i);}for(i=1;i<=n;i++){if(f[i]!=a[i]) ans++;//最后统计答案}cout<<ans<<endl;for(i=1;i<=n;i++){cout<<f[i]<<" ";}cout<<endl;return 0;
}时间复杂度为:O(n);