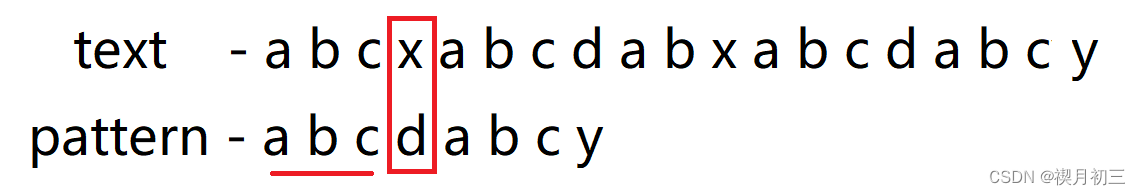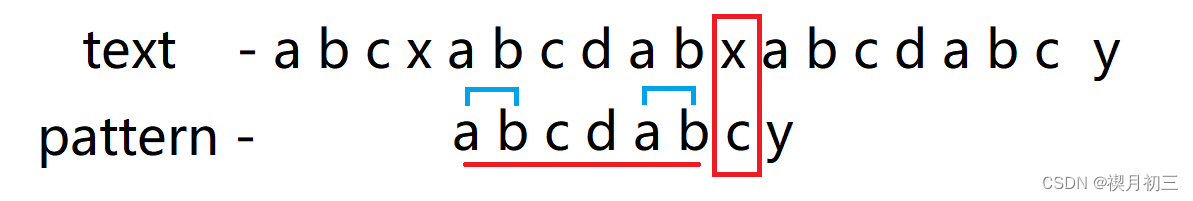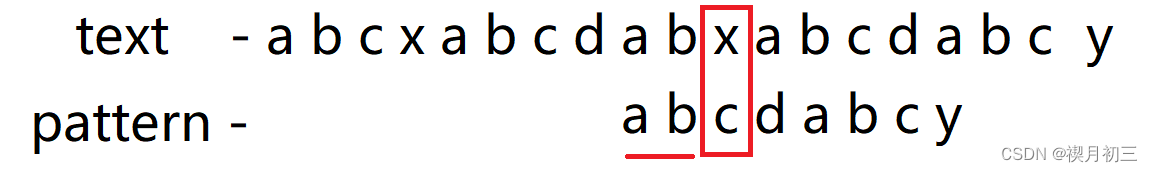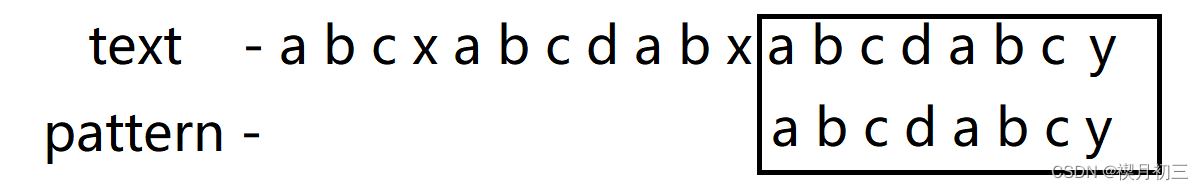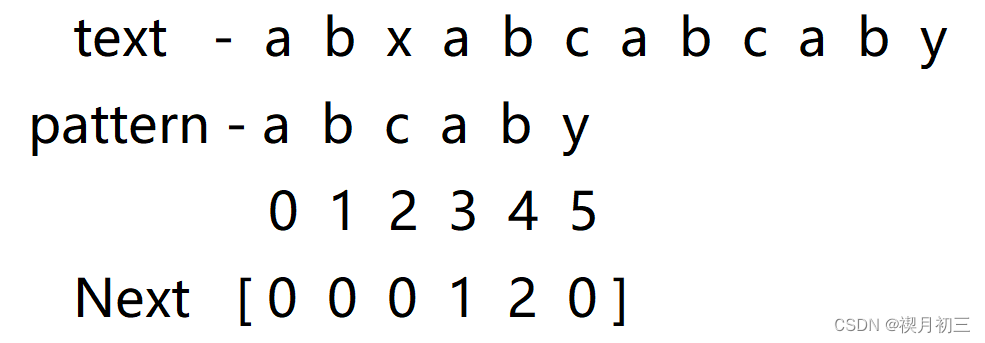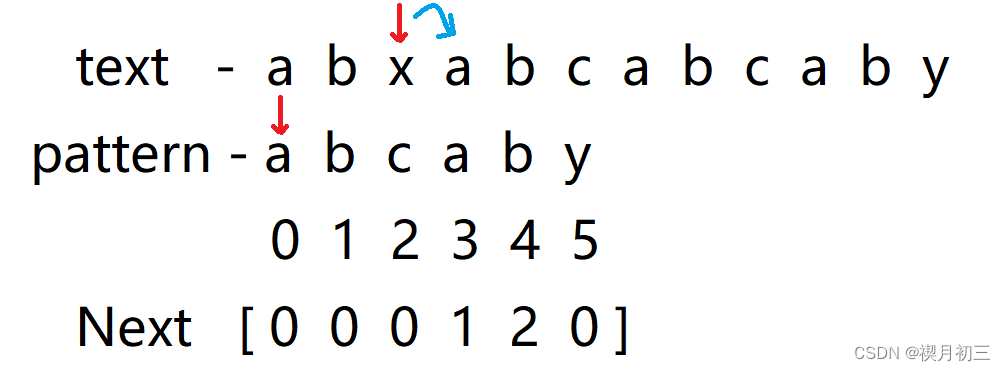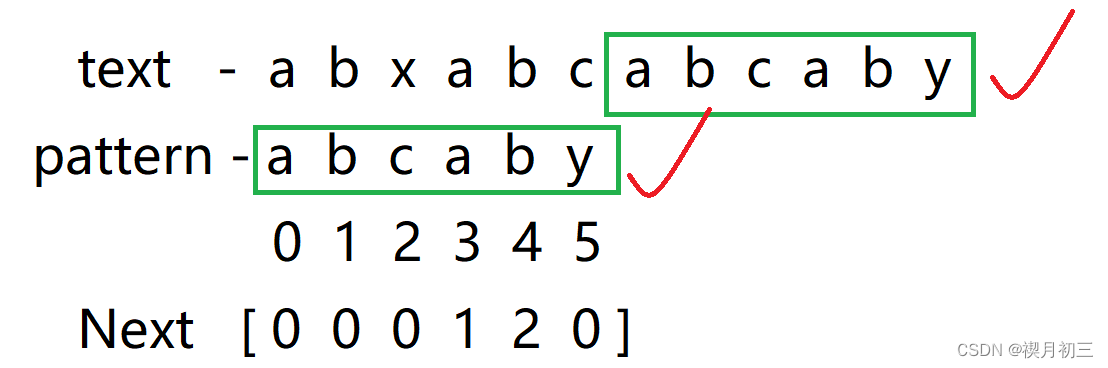数据结构、算法总述：数据结构/基础算法 C/C++_禊月初三的博客-CSDN博客
问题：假设现在我们面临这样一个问题：有一个文本串S，和一个模式串P，现在要查找P在S中的位置，怎么查找呢？
暴力匹配
即2层循环，太过复杂
for (int i = 1; i <= n; i ++ )
{bool flag = true; // 初始化一个标志变量，用于标记是否匹配成功for (int j = 1; j <= m; j ++ ){if (s[i + j - 1] != p[j]){flag=false; // 如果字符不匹配，将标志变量设置为falsebreak; // 并退出内层循环}}
}
时间复杂度：O(m*n)
KMP算法
KMP（Knuth-Morris-Pratt）算法是一种在字符串中查找子串的高效算法，由Donald Knuth, Vaughan Pratt和James H. Morris共同发明。KMP算法的核心思想是，当出现不匹配时，能够利用已经匹配的信息，将模式串合理地向右滑动，跳过一些必然不匹配的位置，从而提高搜索效率。
KMP算法的主要步骤包括两个部分：
- 计算Next[]
- 利用Next[]进行匹配。
理解KMP算法如何运用前缀与后缀的信息：
查找主串(text)中的模式串(partern)
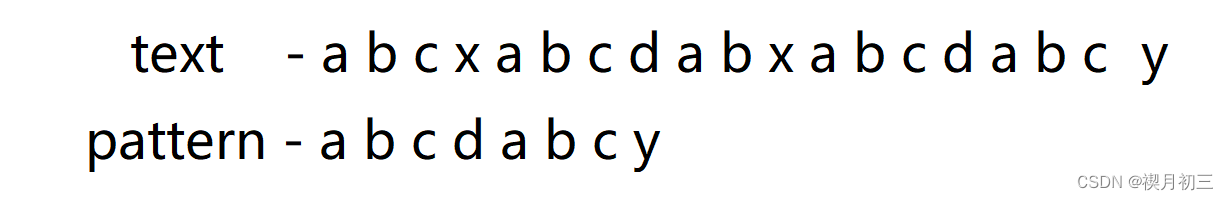
- 从前往后一一匹配，发现x与d不匹配，且d前子串中没有前缀和后缀相同的情况，所以下次将a与x进行匹配，发现不匹配随将其后移一位，使a与a进行匹配；
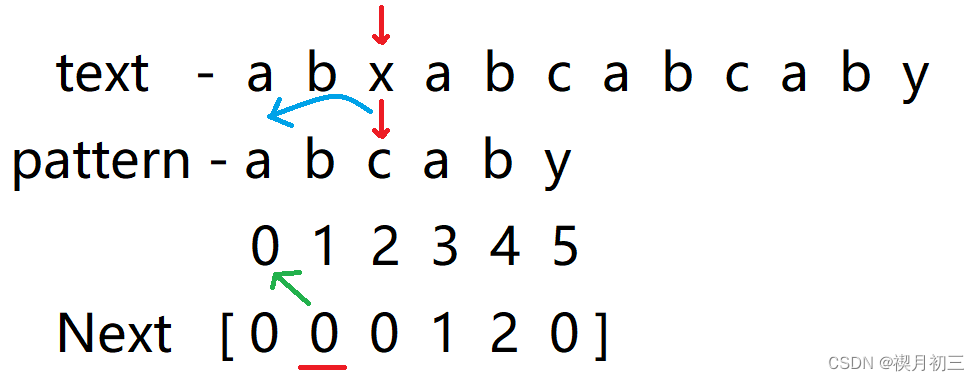
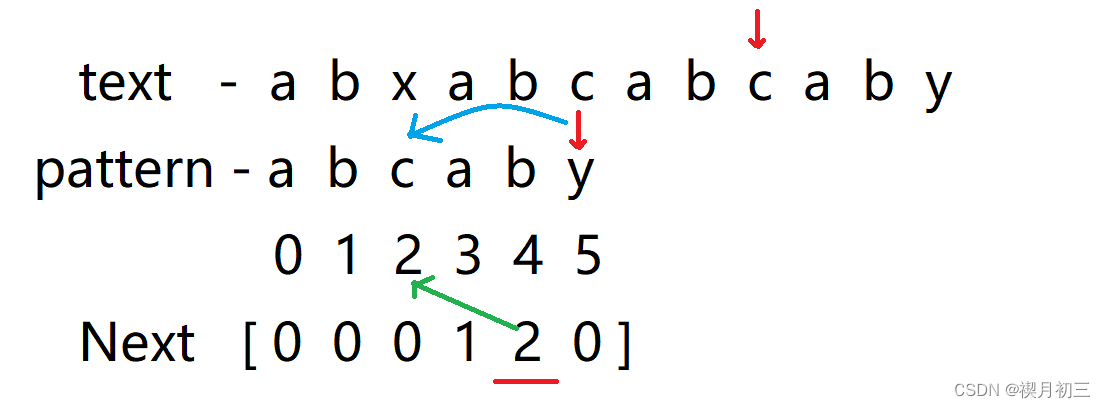
- 从前往后一一匹配，发现x与c不匹配，且c前子串中存在ab为子串相同前后缀（一定要最长的相同前后缀），这意味着x左侧一定与模式串前2位相同为ab，则下次匹配只需将模式串中的c与x进行匹配；
- x与c不匹配，且x前子串中没有前缀和后缀相同的情况,所以下次将a与x进行匹配，发现不匹配随将其后移一位，使a与a进行匹配；
- 从前往后一一匹配,发现匹配完成，即查找到text中pattern的位置。
如何高效的处理前缀与后缀：
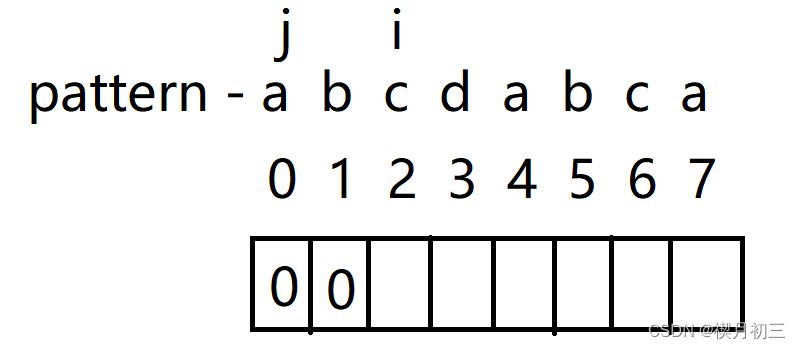
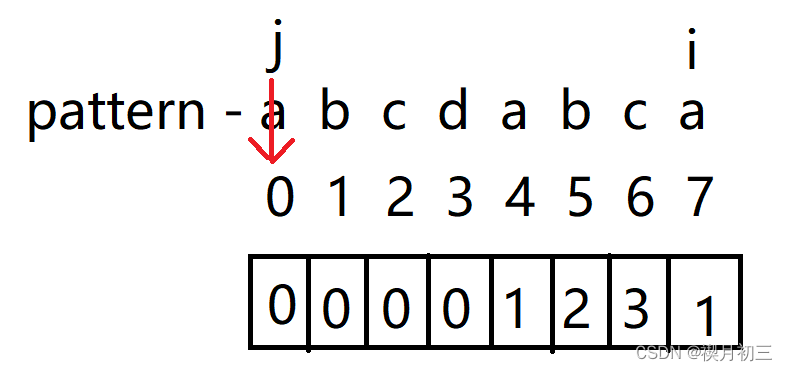
计算Next[]
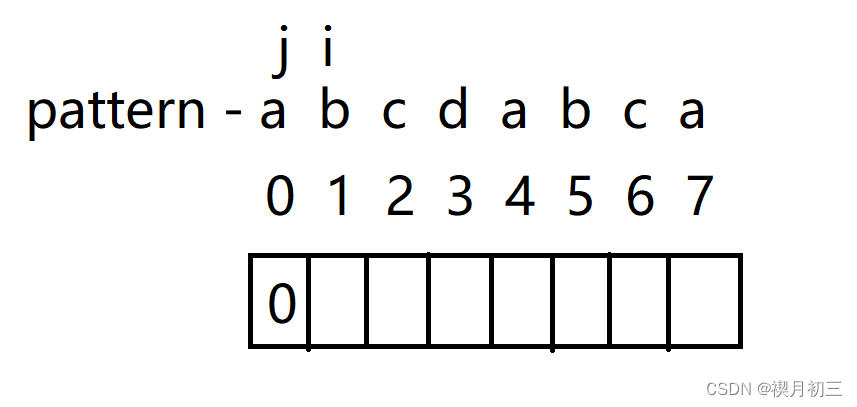
- i与j对应字符不同，将i所对应的字符(b)对应的值计为0，并将i后移；
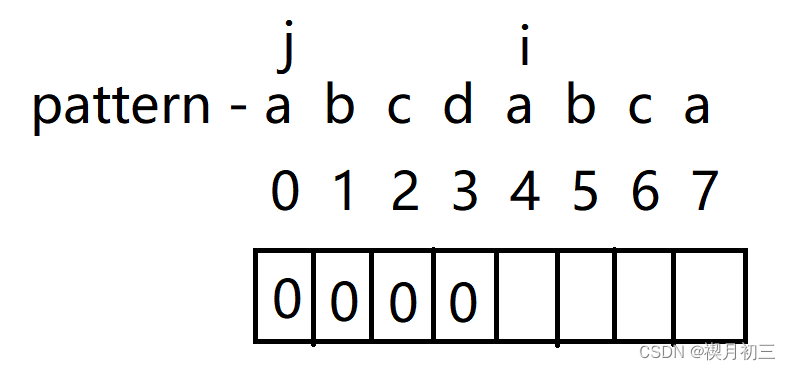
- 同理可得c，d对应值也为0；
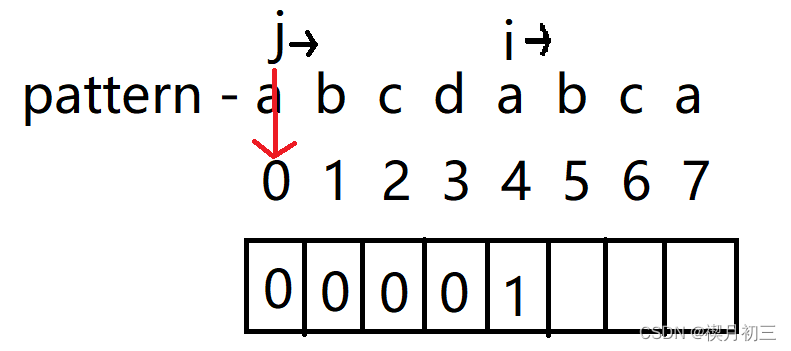
- 当i与j对应的字符相等时，将i对应的值计为j下标+1，并将i，j同时后移；
- 同理可将b，c对应值计算出
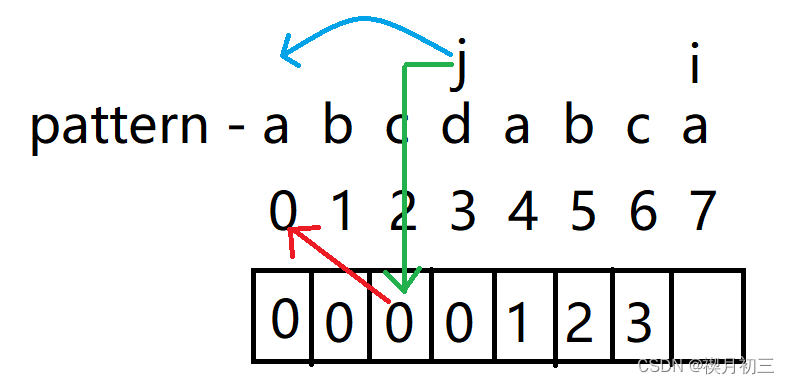
- 当i与j对应字符不同时，看j对应字符的前一个字符所计算的值，并找到pattern中下标与该值相同所对应的字符，并将j前移至该字符；
- 当i， j所对应字符相同时，将j下标+1计为i的值。
eg:
在这个主串和模式串上运用KMP算法：
算法模板
// s[]是主串，p[]是模式串，n是s的长度，m是p的长度
// 求模式串的Next数组：
for (int i = 2, j = 0; i <= m; i ++ )
{while (j && p[i] != p[j + 1]) j = ne[j];if (p[i] == p[j + 1]) j ++ ;ne[i] = j;
}// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{while (j && s[i] != p[j + 1]) j = ne[j];if (s[i] == p[j + 1]) j ++ ;if (j == m){j = ne[j];// 匹配成功后的逻辑}
}时间复杂度：O(m+n)
题目：
831. KMP字符串 - AcWing题库
https://www.acwing.com/problem/content/833/ KMP算法视频参考：
【搬运】油管阿三哥讲KMP查找算法，中英文字幕，人工翻译，简单易懂_哔哩哔哩_bilibili
