Dijkstra算法：求单源最短路径的算法

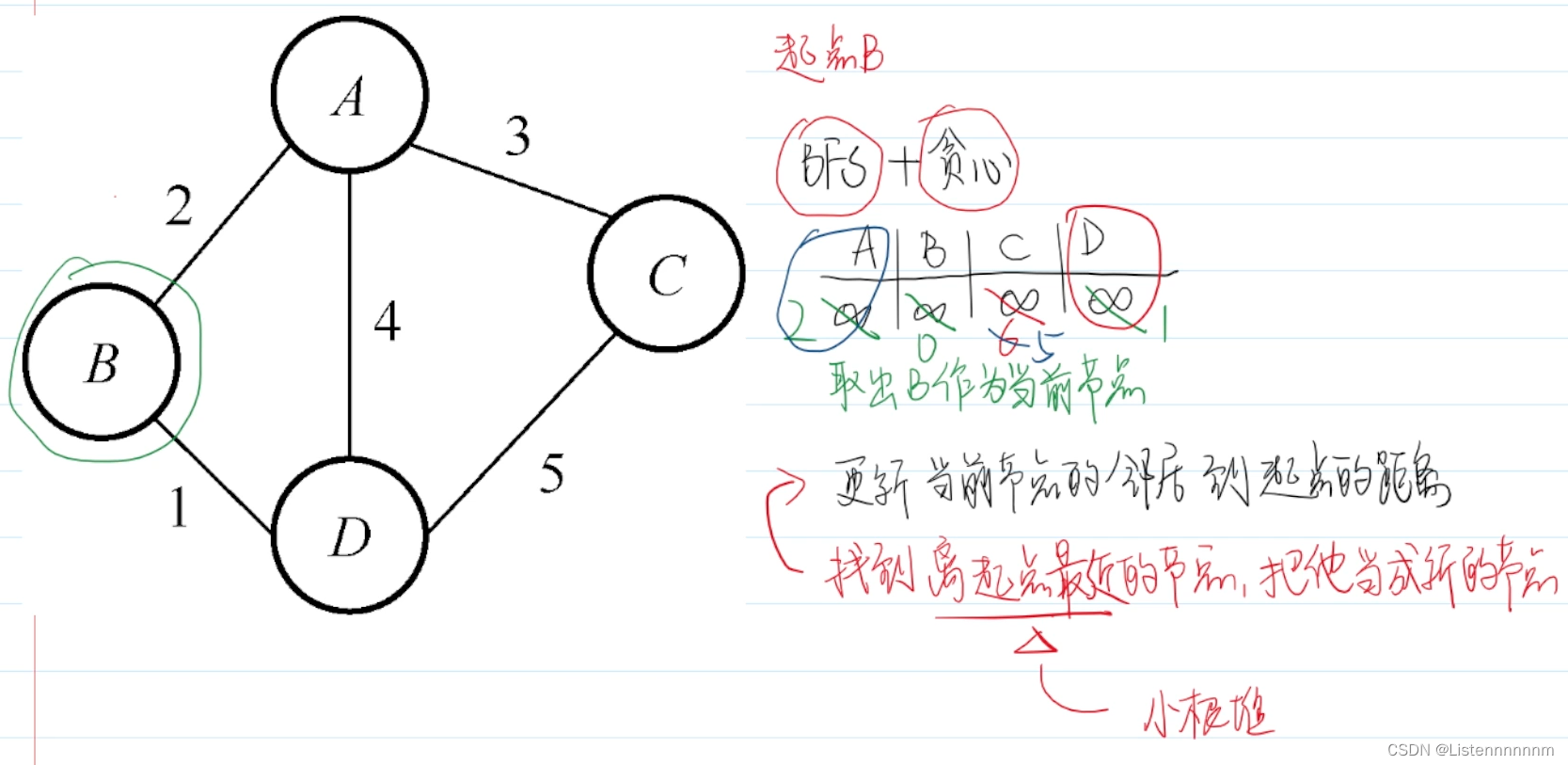
题干

C++实现

#include <stdio.h>
#include <vector>
#include <algorithm>
#include <queue>using namespace std;struct Edge {int u;int v;int weight;Edge(int _u,int _v,int _weight) {u = _u;v = _v;weight = _weight;}
};
vector<Edge> graph[300];struct PQueueNode {int u;//结点编号int distance;//离源点的距离PQueueNode(int _u,int _distance) {u = _u;distance = _distance;}
};//自定义类型不支持<运算符，所以要运算符重载
bool operator<(PQueueNode lhs,PQueueNode rhs) {return lhs.distance > rhs.distance;
}int Dijkstra(int s,int t) {//准备一个优先队列，保存下一个将要访问的结点priority_queue<PQueueNode> pqueue;//就是小根堆，每次出队的都是距离最小的结点int distance[300];int isVisited[300];for(int i = 0; i<300; i++) {distance[i] = -1;isVisited[i] = false;}//起点进入小根堆distance[s] = 0;PQueueNode qnode(s,0);pqueue.push(qnode);while(pqueue.empty() == false) {int u = pqueue.top().u;pqueue.pop();if(isVisited[u] == true) {continue;}isVisited[u] = true;//遍历所有邻居，加入队列for(int i = 0; i<graph[u].size(); ++i) {int v = graph[u][i].v;int weight = graph[u][i].weight;if(distance[v] == -1 || distance[v] > distance[u] + weight) {distance[v] = distance[u] + weight;PQueueNode next(v,distance[v]);pqueue.push(next);}}}return distance[t];
}int main() {int n,m;while(scanf("%d%d",&n,&m) != EOF) {for(int i = 0; i<n; ++i) {graph[i].clear();}for(int i = 0; i < m; ++i) {int u,v,weight;scanf("%d%d%d",&u,&v,&weight);Edge e1(u,v,weight);graph[u].push_back(e1);Edge e2(v,u,weight);graph[v].push_back(e2);}int s,t;scanf("%d%d",&s,&t);printf("%d\n",Dijkstra(s,t));}return 0;
}