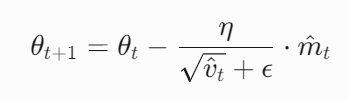08 梯度消失与梯度爆炸问题

news/2025/2/26 17:49:17/文章来源:https://www.cnblogs.com/wangle1006/p/18739214

由反向传播原理可知，梯度的计算遵循链式法则。由于网络层数不断加深，梯度的连乘效应可能会导致梯度呈指数形式衰减，又或以指数形式增加。
前者叫做梯度消失，梯度消失导致网络中的早期层几乎不更新，使得网络难以学习到输入数据的有效特征。可能导致网络权重更新非常缓慢，使得训练过程变得不稳定。
后者叫做梯度爆炸，梯度爆炸会导致权重更新过大，使得网络在训练过程中跳过最优解，无法收敛。

1. 可能导致梯度消失/爆炸的原因

激活函数的选择

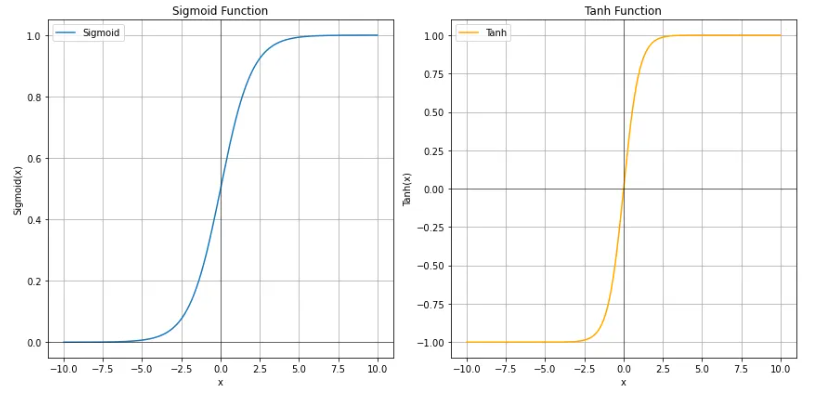
常用的sigmoid和tanh激活函数的梯度小于1，尤其是sigmoid函数其导数最大为0.25。在深度网络中，经过多个层的反向传播后，梯度会乘以这些小的导数值，导致梯度指数级减小。

权重初始化

如果权重初始化过小，乘积效应会导致梯度在传播过程中迅速减小。如果权重初始化过大，那么在反向传播过程中，梯度的计算会受到很大的影响，容易导致梯度爆炸。例如，如果权重由标准正态分布初始化，其期望数量级为1，那么在多层传播后，梯度值可能会变得非常大。

学习率设置

学习率决定了模型参数更新的步长。如果学习率设置得过高，那么模型参数在更新时可能会因为步长过大而跳出最优解的范围。同时，过高的学习率会使模型在更新参数时过于激进，从而加剧梯度的波动，导致梯度爆炸。

深度网络的层次

在非常深的网络中，梯度必须通过多个层传播。每经过一个层，梯度都会乘以该层的权重导数。如果这些乘积都很小，最终梯度会趋向于零；如果每一层的梯度都稍微增大一点，那么经过多层传播后，梯度值就会变得非常大，从而导致梯度爆炸。因此，网络层数的增加会加剧梯度消失/爆炸的风险。

2. 梯度消失/爆炸的一些解决方法

替换激活函数

如将sigmoid替换成Relu等，因为Relu的导数在正数部分恒等于1，不会出现梯度消失和爆炸的问题。

权重初始化

合理的权重初始化方法（如He初始化或Xavier初始化）可以帮助防止梯度消失或爆炸。
Xavier初始化方法根据输入和输出神经元的数量来调整权重的初始值，使得前向传播和反向传播中的激活值和梯度值保持相近的方差，适用于sigmoid等激活函数。
He初始化针对ReLU及其变种，能使权重在正向和反向传播中保持合适的方差，确保梯度有效传递。

权重正则化

如L1和L2正则化可以限制权重的大小，减少梯度爆炸的风险。L1正则化通过给参数增加绝对值约束来鼓励参数稀疏化；L2正则化则通过给参数增加平方约束来鼓励参数值接近0。
正则化不仅可以防止模型过拟合，还可以在一定程度上缓解梯度爆炸问题。因为通过给参数增加约束项，可以限制参数在更新过程中的取值范围，从而避免梯度因参数值过大而爆炸。

梯度剪切

梯度裁剪是一种有效的解决梯度爆炸的方法。它的基本思想是在每个训练步骤后检查梯度的范数（或某些权重的范数），如果超过了某个阈值，就将梯度进行缩放，从而限制梯度的大小。这样可以防止梯度在反向传播过程中无限增长，导致网络不稳定。

BN（批量归一化）

批归一化（Batch Normalization）是一种通过在每层的输入上对数据进行标准化来减少梯度变化的方法。它通过对当前小批次的均值和方差进行归一化，使得每一层的输入分布保持稳定。这样可以有效缓解内部协变量漂移（Internal Covariate Shift）现象，即每一层的输入分布随着网络参数的更新而发生变化的现象。批归一化不仅有助于提高网络的训练速度和稳定性，还可以在一定程度上缓解梯度爆炸问题。因为通过归一化处理，每一层的输入数据的分布变得更加稳定，从而使得梯度的变化也更加平稳。