(done 剩个什么 3/4 unigram frequency 的玩意儿没懂) word2vec 算法，计算嵌入矩阵（CBOW, Skip-gram）随机梯度下降法 SGD 负采样方案-编程知识

参考视频1：https://www.bilibili.com/video/BV1vS4y1N7mo/?vd_source=7a1a0bc74158c6993c7355c5490fc600 （讲的太浅了）

参考视频2：https://www.bilibili.com/video/BV1s64y1P7Qm?p=4&vd_source=7a1a0bc74158c6993c7355c5490fc600 (Stanford CS224n 词向量那堂课) (非常棒的理论课)

参考视频3：https://www.bilibili.com/video/BV1MS4y147js?p=4&vd_source=7a1a0bc74158c6993c7355c5490fc600 (这个讲得很含糊，看完没懂)

还有一个不知道从哪里看到的 slide

参考视频4：https://www.bilibili.com/video/BV1s64y1P7Qm?p=5&vd_source=7a1a0bc74158c6993c7355c5490fc600 (还是斯坦福教授讲得深入浅出、通俗易懂)

还有一些不知道从哪里看到的 slides

word2vec 算法基于一个重要假设：文本中离得越近得词语相似度越高
意思就是，在人类语言中，经常一起出现的单词有一定的相似性
比如这句话 “I love you”
可以认为 “I” “love” “you” 这三个单词有一定的相似性
在这里插入图片描述

理论部分 (来自 Stanford CS224n)

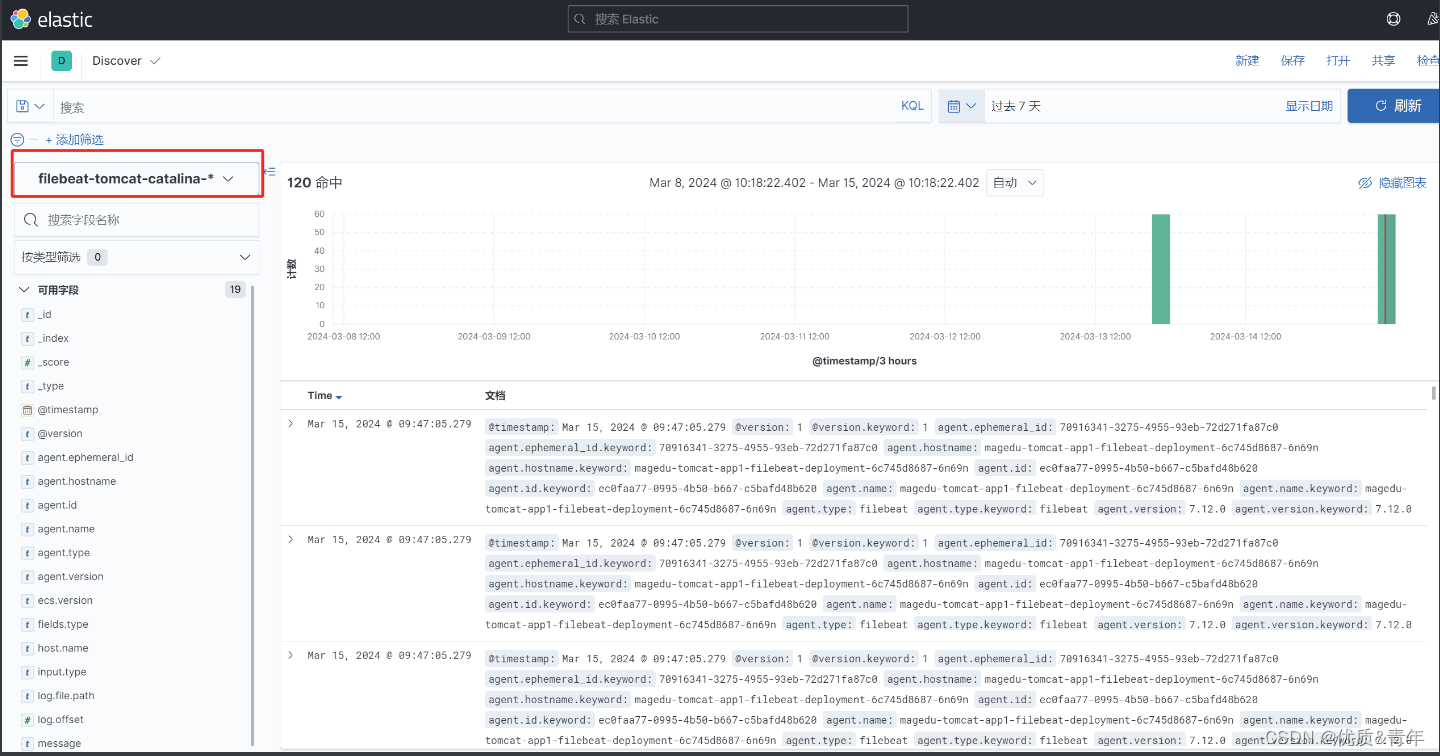
一个基本的思想是，一个单词的意思并不是由这个单词单独给出的，还由它周围的单词一起给出
因此，当我们构建单词 “banking” 的 representation 时，我们要使用它的上下文 context 一起构建
在这里插入图片描述

单词向量 (word vectors) 也有另一个名字 “词嵌入 (word embeddings)” ，或者叫 “神经单词表示 (neural word representation)”
如下图，我们使用一个实数矢量来表示单词 “banking”，那么这个实数矢量是怎么得出的呢？
在这里插入图片描述

以下是词嵌入算法 word2vec 的介绍
大致思想总结如下：
1.词汇表/语料库中的每一个单词都是用一个实数矢量表示
2.当我们扫描一个句子时，用 Vc 表示中心词，它周围的词 Vo 表示上下文词
3.我们的要求是，词义越接近的单词，它们的矢量应该越接近，这个矢量的距离就是 “假设矢量长度被正则化，则距离是夹角”
4.同时，我们希望可以使用中心词的矢量去预测它的上下文单词出现的概率
注意：实际上，余弦距离就是 cos(theta)，这里的 theta 就是两个矢量的夹角
在这里插入图片描述

在训练 word vectors 的过程中，我们会定义一个窗口 window
我们扫描训练集的句子时，锚点就是中心词 Vc，它的上下文是 Vo
在下图来看，Wt 就是中心词，而 Wt+j 就是上下文单词
P(Wt+j | Wt) 就是，当中心词 Wt 出现时，上下文单词 Wt+j 出现的概率
我们训练 word vectors 的指标，就是让 P(Wt+j | Wt) 尽可能符合我们的训练集情况
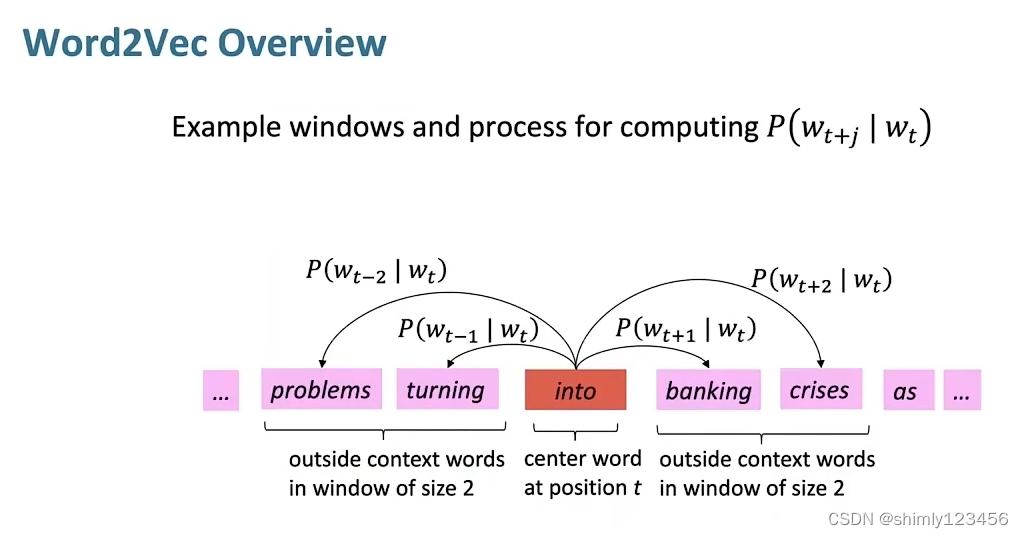
在这里插入图片描述

如此一来，就能写出如下图所示的似然函数
而我们要做的就是，找到能够让似然函数最大化的 “参数”，这个参数也就是语料库/词汇表中所有单词的 word vectors
加上 log，再加上负号(-)，我们就得到了目标函数，也可以叫做代价函数，或者损失函数
训练 word vectors 的过程，就是不断调整 word vectors，来减少 loss function
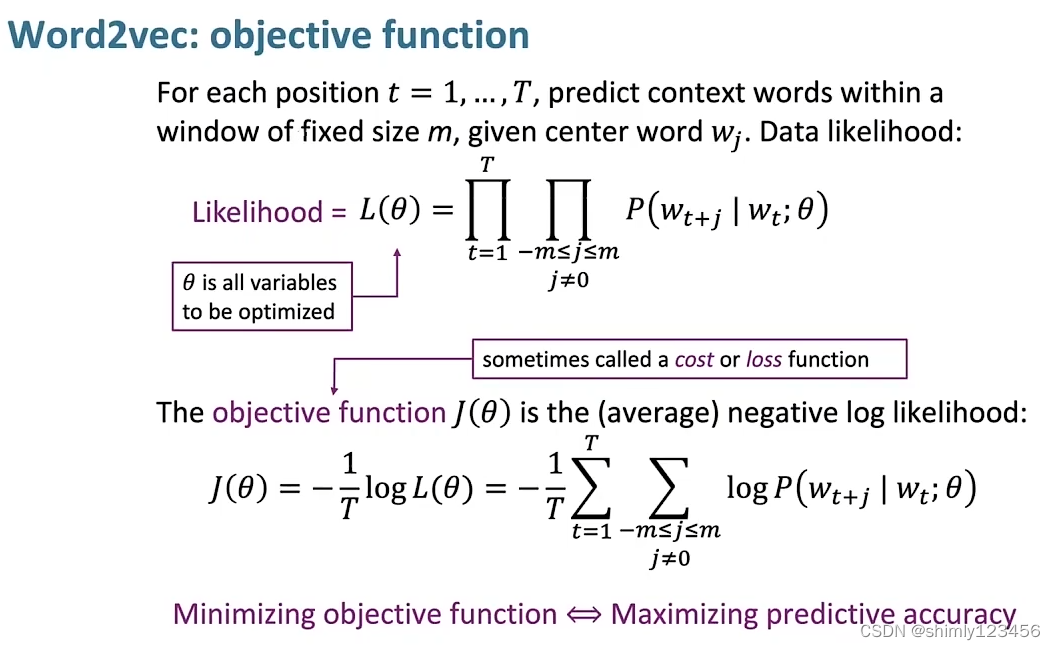
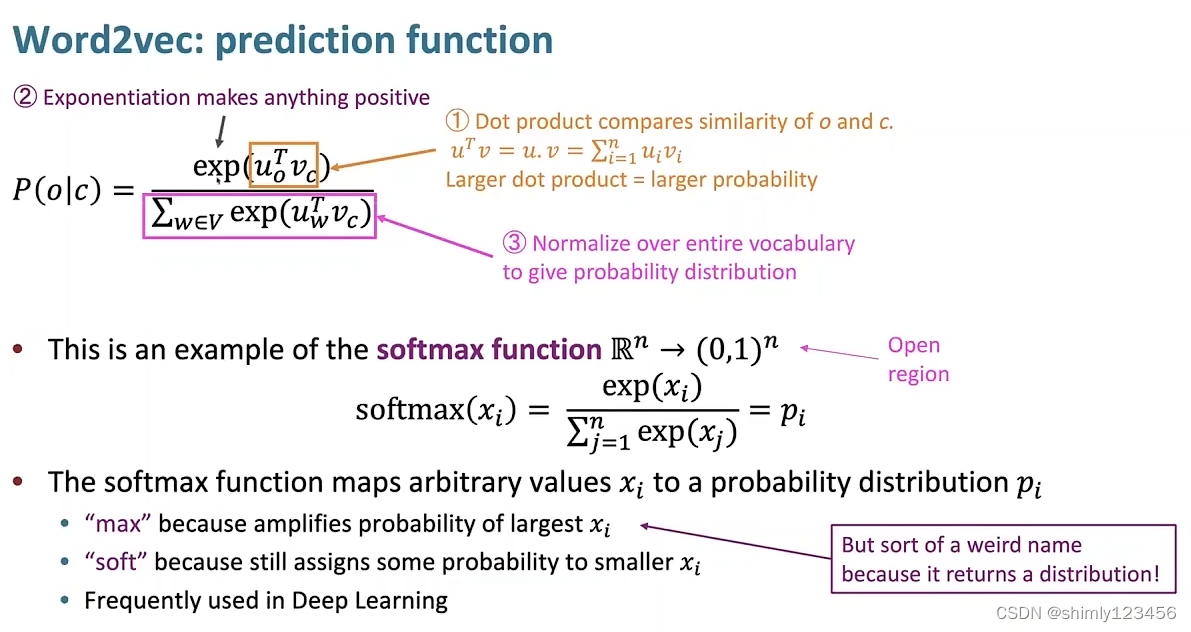
在这里插入图片描述

那么现在，有一个问题，怎么表示 P(Wt+j | Wt ; theta) ？
如下图，Stanford Chris Manning 所使用的公式有点像 softmax 函数
这里有个符号需要说明
Vw：当单词 w 是中心词时的矢量
Uw：当单词 w 是上下文词时的矢量
在这里插入图片描述

如下是聪明老头使用这个公式的理由
1.Uo’ Vc 的意义是使用 “中心词矢量” 和 “上下文词矢量” 做内积。这个是有实际意义的，在矢量长度被正则化的前提下，两个矢量越接近，那么它们内积的值就越大
2.使用 exp() 的原因：这是一个自然数指数函数，它的作用就是把实数域映射到 (0, 正无穷)，即 R —> (0, 正无穷)
3.最后再使用整个词汇表的单词，对 Vc 做内积，进行一个正则化
这也是 softmax 函数的名字的来由：max 表示这个公式会放大最大的上下文单词的概率，soft 表示这个公式依然会分配一些概率给可能性较小的上下文单词
在这里插入图片描述

搞明白了 P(Wt+j | Wt ; theta) 的公式后，代入之前的似然函数，我们就有了训练 Word Vectors 所使用的损失函数
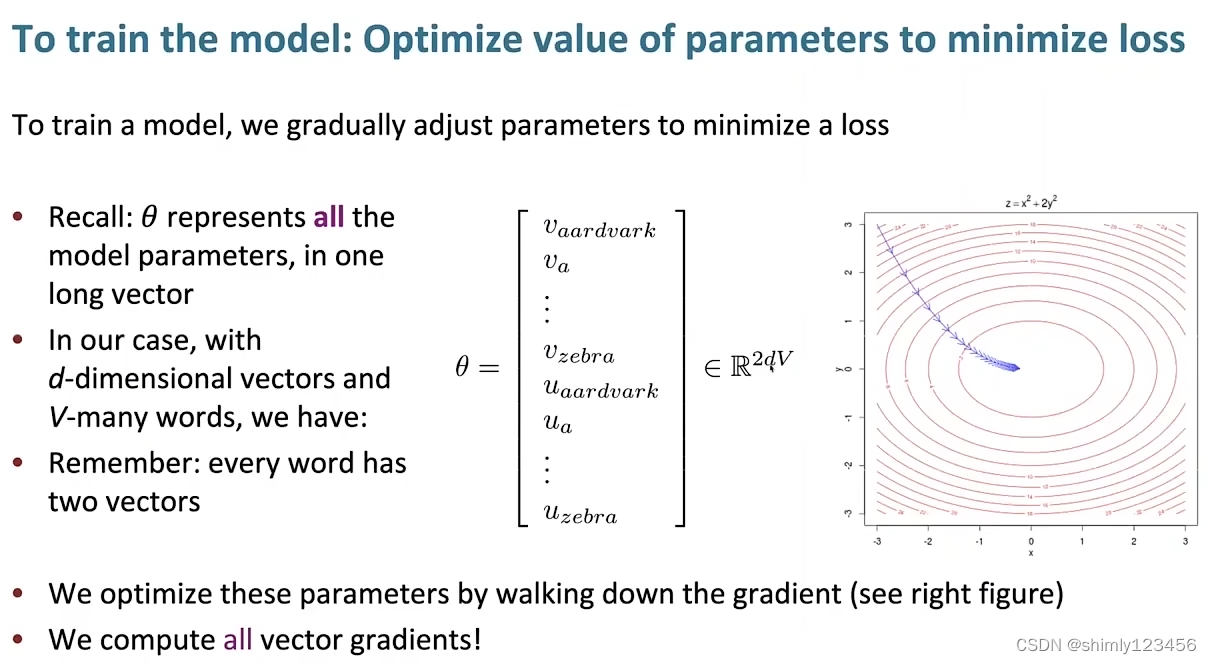
那么还有一个问题，theta，即我们要训练的参数是什么？
答案就是把所有单词矢量连接起来的一个超长矢量
假设单词总共有 V 个，每个单词使用一个 d 维矢量来表示，每个单词分别有一个中心词矢量Vc 和一个上下文矢量Uc
那么 theta 的维度就是 2dV
如此一来，theta 和损失函数都有了，假如这是一个凸函数，那我们就可以使用梯度下降法去计算最优的 theta 了
在这里插入图片描述

既然使用了梯度下降法，那么自然涉及到对损失函数的求导，让我们来求导试试
经过求导，我们可以根据求导结果来评判目前模型的好坏
在这里插入图片描述

理论部分到此为止

接下来让我们看看那个 slide，如下图
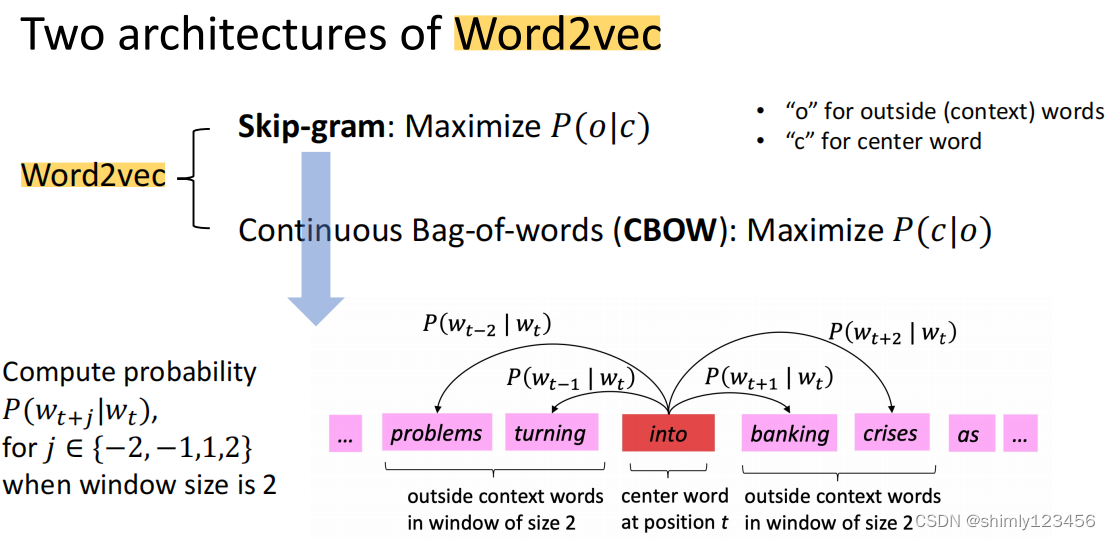
在这里插入图片描述

Word2vec 算法一共有两种，分别是 1. skip-gram 2. CBOW

我们在前面两个部分展示的理论是 skip-gram，即，当中心词出现时，计算上下文词出现的概率

CBOW 正好相反，计算当上下文词出现时，中心词出现的概率

接下来看看第三个视频

如下图，简单明了地展示了 CBOW 和 Skip-gram 两个模型的异同
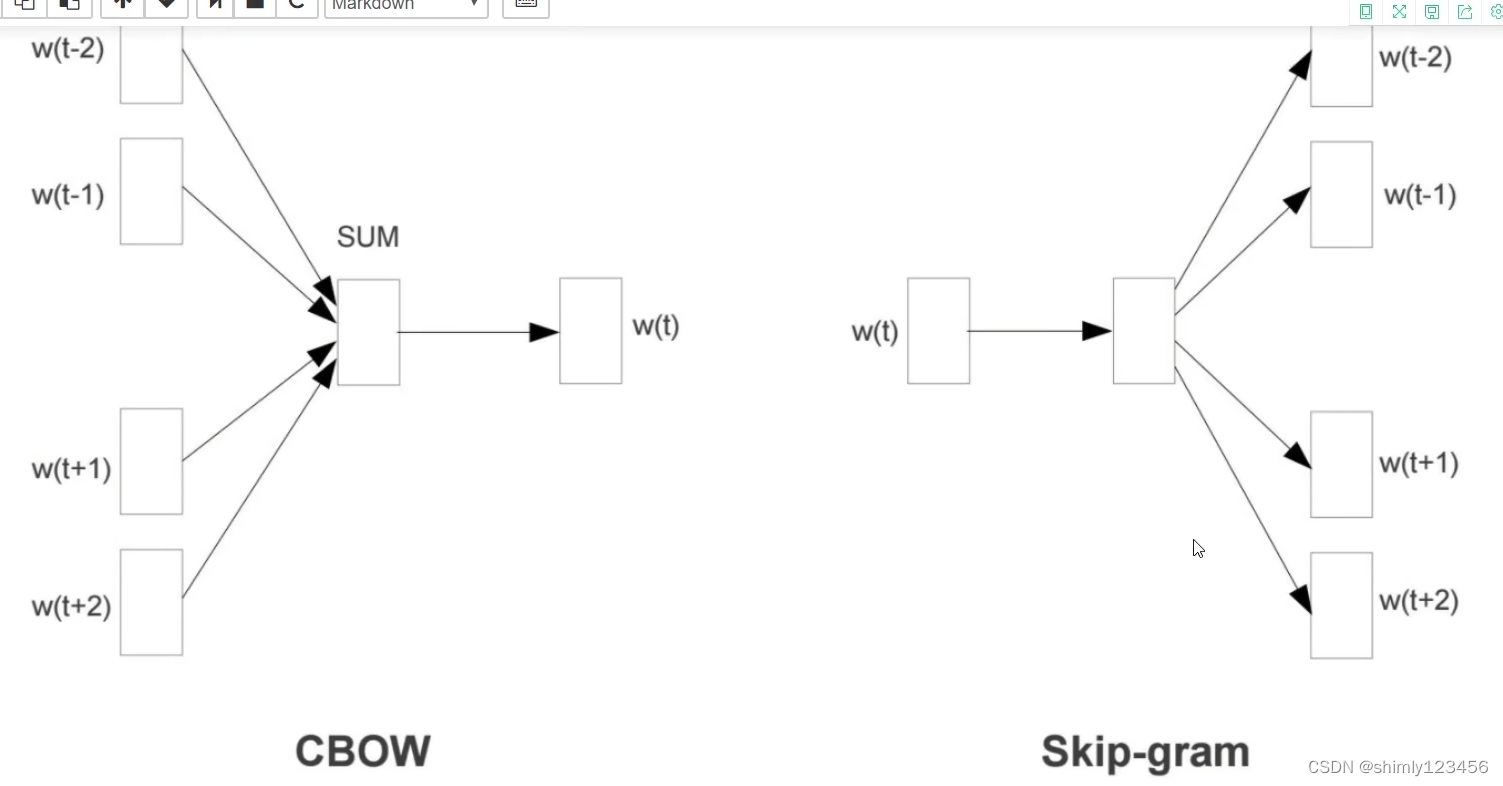
在这里插入图片描述

剩下的内容看不懂，就当作是老师讲得太烂了

接下来我们看看斯坦福教授的讲课（参考视频4），主要是看看什么是 “负采样方案”

训练 word vectors 的一开始，我们会随机初始化所有的 word vectors
随后，我们会逐个迭代语料库中的每个单词
尝试使用 P(o | c) 那个公式去预测每个单词(作为中心词) 的上下文词
此时，我们需要更新单词矢量，来让它们能够更好的预测 “上下文词”
这里有个问题：为什么同样类型的单词，它们的矢量方向会更接近？原因：它们的上下文单词预测情况接近
在这里插入图片描述

恰恰是因为同类型单词作为中心词时，上下文单词的预测情况大致相同，因此当我们把 word vectors 映射到二维平面上时，可以看到语义类似的单词靠得比较近，如下图
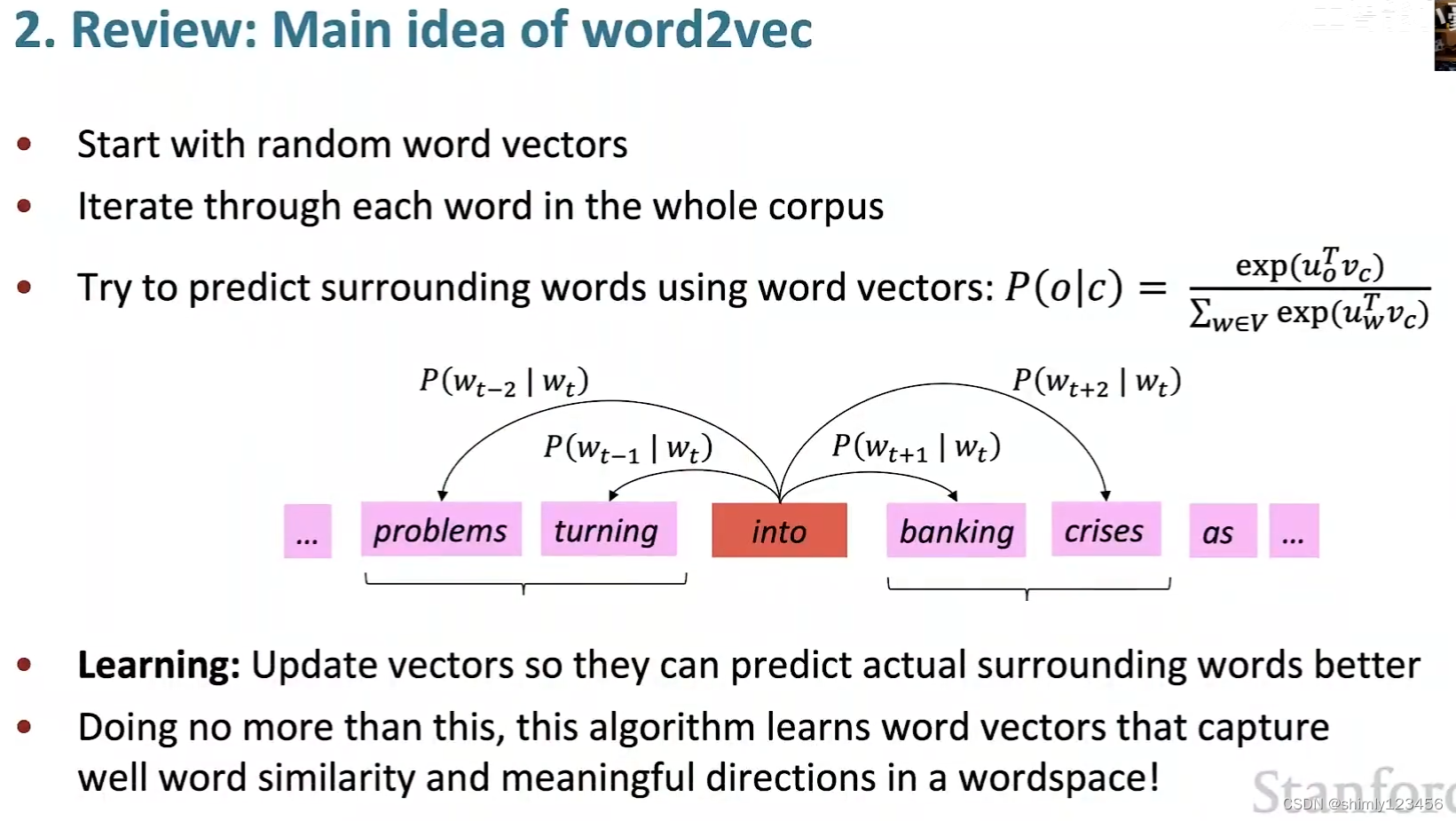
在这里插入图片描述

这里稍微讲一下 word vectors 预测 surrounding words 的计算过程，如下图
U 是语料库中所有单词的 “作为上下文单词时的单词矢量矩阵”
V 是语料库中所有单词的 “作为中心单词时的单词矢量矩阵”
当一个单词 V4 被作为中心单词，我们要获取语料库中每个单词作为上下文单词出现的概率时，计算 softmax(U V4’)，即可计算出语料库中每个单词作为上下文单词出现的概率
在这里插入图片描述

这里是对损失函数 J(theta) 进行优化的一个案例，我们所使用的是 “梯度下降法”。
这里实际上使用的是 “批次梯度下降法”，因为损失函数 J(theta) 使用了整个语料库中的单词。
在实践中，语料库通常非常庞大，因此不能使用这种 “全批次梯度下降法”，而是通常使用 “随机梯度下降法” 或者 “小批次梯度下降法”。
需要注意的是，在优化过程中，stepSize 的设置要非常注意，设置得太大或者太小都会影响训练效果
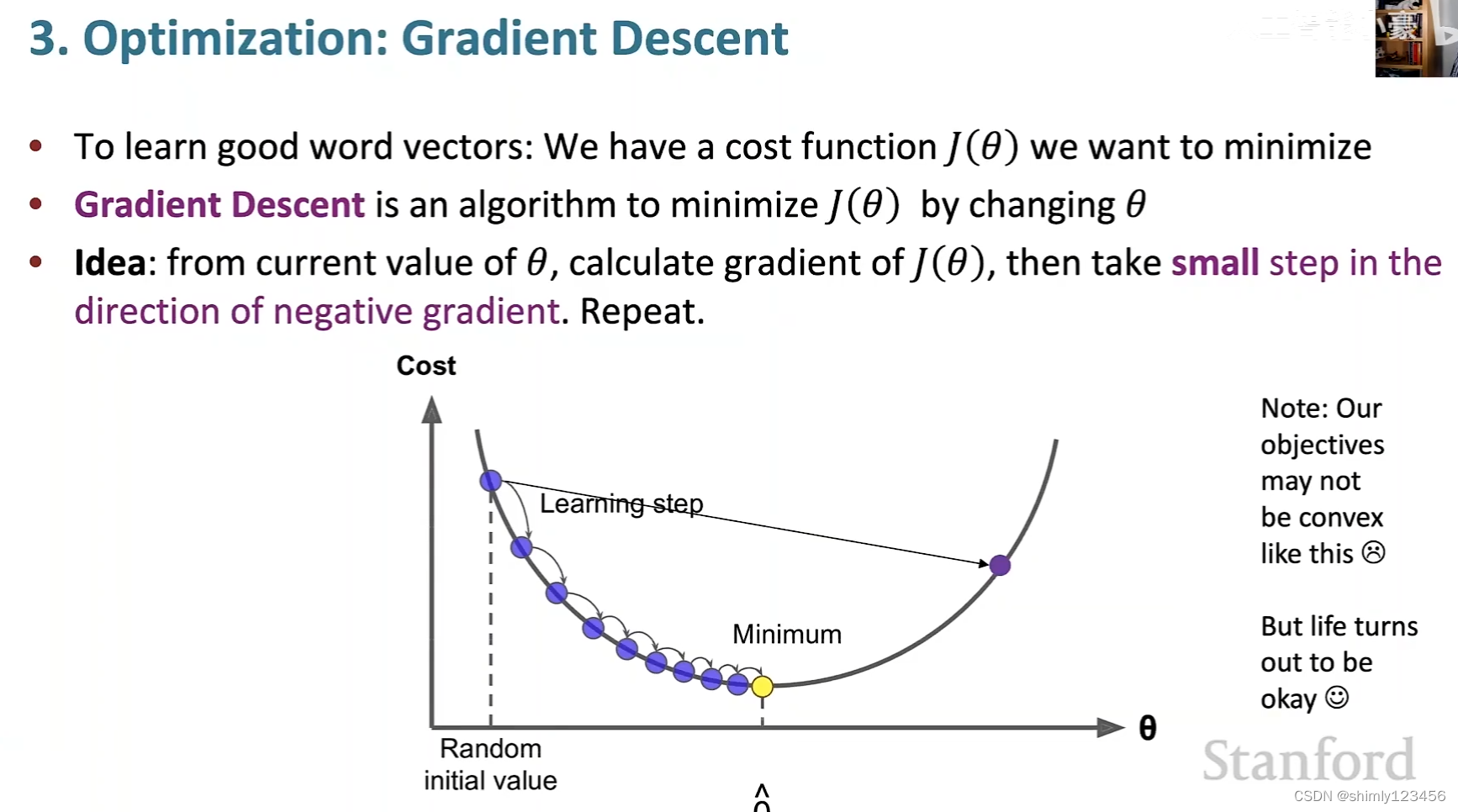
在这里插入图片描述

如下图是梯度下降法一个典型的更新参数矩阵的过程
这种简单的 “全批次梯度下降法” 几乎没有人使用
在这里插入图片描述

由于简单梯度下降法会使用整个语料库来进行一次参数的更新，在语料库很大时，简单梯度下降法的每一次更新参数都会变得非常昂贵
因此，更 practical 的方式是使用随机梯度下降法 SGD Stochastic Gradient Descent
这种方法其实很简单：每次只从整个语料库里选取一部分，使用这一部分样本构造损失函数 J(theta)，然后计算这个 J(theta) 的梯度，再使用这个梯度来更新参数矢量
在这里插入图片描述

接下来让我们研究一下 “负采样方案” 是他妈的甚？

根据远在天国的奶奶给我寄来的 “不明来源 slides”，我们可以看到，当前使用的 word2vec-skipgram 算法存在一些问题，如下两个slides
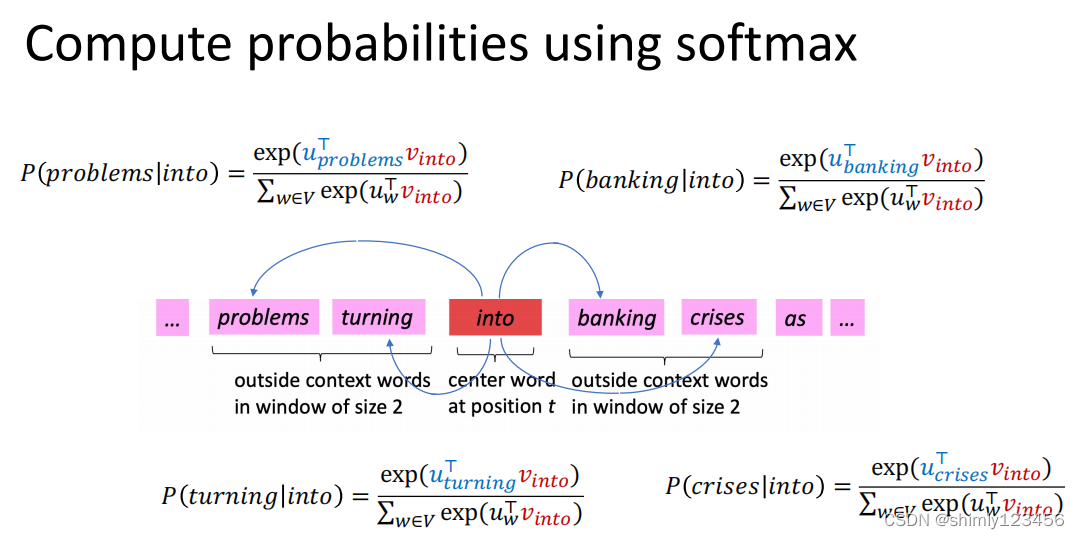
在这里插入图片描述

当我们把单词 “into” 作为中心词时，计算其它单词作为 “上下文词” 出现的概率时，我们在计算分母的时候涉及到了大量计算

假设语料库有 10000 个单词，那么这里就涉及到了 10000 次内积计算

也就是说，计算每个 P(o|c)，我们都需要计算 m 次内积 (m = 语料库的单词数量)。无论是在模型的 predict 功能上，还是在模型的 training 过程中，这都会导致相当大的开销。

解决方案有两个，如下图
方案1–层次化softmax：把 P(o|c) 的计算拆成多个概率的乘积 P(o < 5k | c) x P(o < 2.5k | c) x … 这样一来就可以把多个 softmax 计算拆成多个 sigmoid 计算的相乘，而 sigmoid 函数明显比 softmax 函数开销要少得多。这样一来，我们就把一个 softmax 计算拆成了 log(|V|) 个 sigmoid 计算。
方案2–负采样：这似乎是更加 popular 的方案，详情看后面的 slides
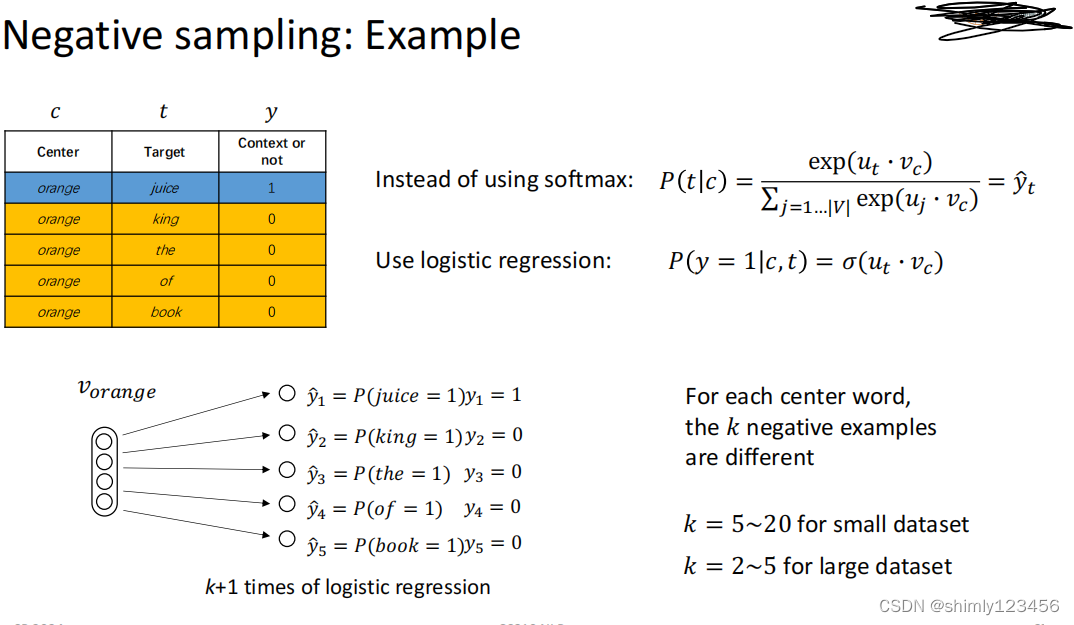
在这里插入图片描述

负采样方案的思想是：我在训练 word vectors 的时候，选取中心词后，在选取上下文单词时，我除了选一个在训练集中确实能看到的 surrounding words 作为上下文单词，还可以选一些确实在训练集中不是当前中心词的 surrounding words 的单词。随后给它们打上标签 0 和 1
在这里插入图片描述

接着，我们可以最大化下面的 log-似然函数
可以看到，总的 J(theta) = …
里面小的 Jt(theta) = …
这个似然函数相比之前的优点是：它把 softmax 计算转成了 sigmoid 计算，大大降低了计算开销
那么为什么这种似然函数会有用呢？我们看后面的 slides
在这里插入图片描述

那篇 2013 年的 paper 又臭又长，人生苦短，我们直观理解一下就好
蓝圈圈的部分表示：当我们在最大化 Jt(theta) 时，我们需要最大化蓝圈圈的部分，此时我们就是在最小化 Uo 和 Vc 两个向量之间的余弦距离，让它们尽可能接近
而橙色圈圈的部分表示：当我们在最大化 Jt(theta) 时，我们需要最小化橙色圈圈的部分，此时我们就是在最大化 Uwi 和 Vc 两个向量之间的余弦距离，让它们尽可能远离 (因为前面有负号 “-”)
在这里插入图片描述