🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972

   个人介绍: 研一｜统计学｜干货分享
         擅长Python、Matlab、R等主流编程软件
         累计十余项国家级比赛奖项，参与研究经费10w、40w级横向

熟悉eviews基本操作,利用eviews建立粮食产量和劳动力及化肥之间的简单线性回归模型,并根据回归结果进行数据解读。文章涉及普通最小二乘法、F检验、t检验、多重共线性检验、模型修正、相关可视化及解析。

1 数据背景

  我国1975-2000年粮食产量、劳动力和化肥使用量数据，数据来源于实验课数据文件，具体数据下表所示。

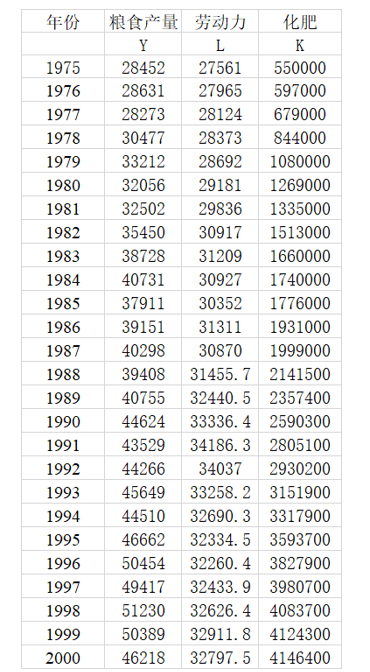
  由于生产函数具有一个最大特征：能够刻画要素的边际效益递减规律，即当其它要素投入不变时，随着某一要素的投入量增加，获得的产出增量越来越少。由C-D生产函数：

$$Y=A{K}^{{\beta }_1}{L}^{{\beta }_2}$$

2 理论模型

  该问题理论模型为：

$$ln(Y)=\alpha +{\beta }_{1}ln(L)+{\beta }_{2}ln(K)+\mu$$

  其中Y表示粮食产量，L表示劳动力，K表示化肥使用量。

3 粮食产量关系线性图

  粮食产量关系线性图如下：

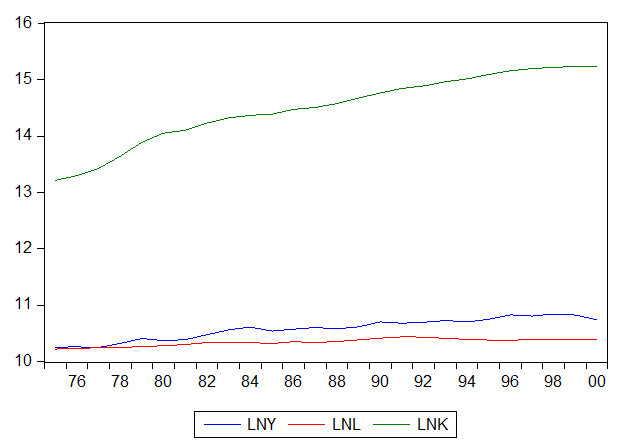
  由上图可以看出，随着年份的增加，我国1975-2000年粮食产量、劳动力和化肥使用量经对数化后逐渐趋于平稳。

4 模型求解

  通过Eviews10.0软件进行回归得到结果：

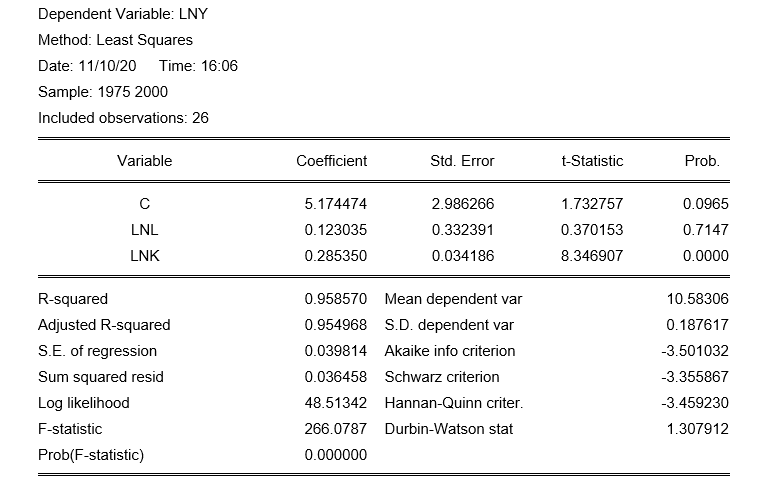
  根据结果显示，得到初步回归函数：

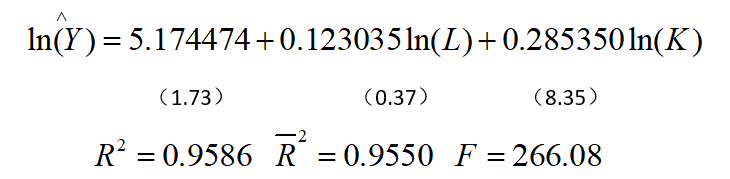
  回归方程Prob(F-statistic)=0.000000<0.05,通过显著性水平为0.05的显著性检验。

  回归结果表明$ln(Y)$变化的95.9%可由劳动力和化肥投入的变化来解释。在0.05的显著性水平下，F统计量的临界值$F_{0.05}(2,23)=3.42<266.0787$，表明模型的线性关系显著成立。自由度n-k-1=23时，的t检验统计量$t_{0.05}(23)=2.069$，因此，$ln(L)$未通过显著性检验，$ln(K)$的参数显著地异于0，考虑存在多重共线性。

5 多重共线性检验

  相关系数表如下：

  由检验结果显示，LNL、LNK的相关系数达0.9263，存在严重多重共线性。

6 模型修正

  利用逐步回归法消除多重共线性，结果如下：

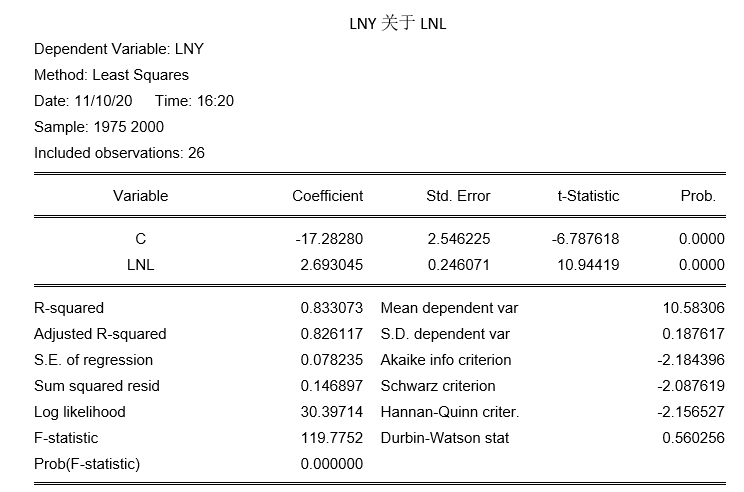
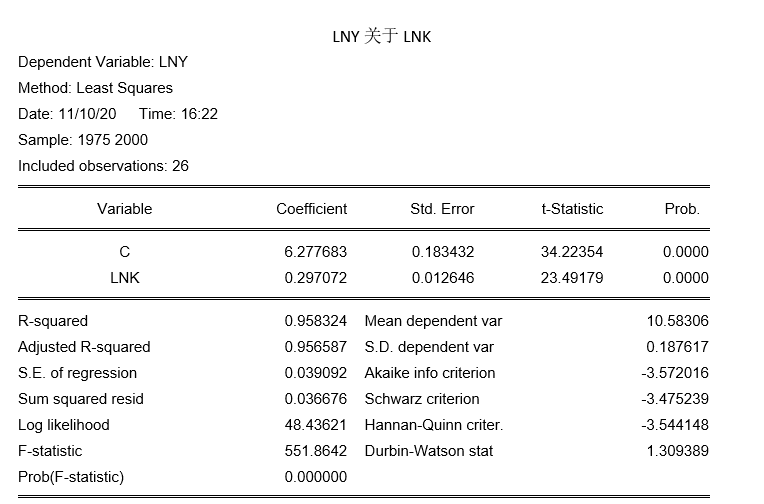
  根据结果显示，选取LNY关于LNK的函数拟合优度更好，即回归方程为：

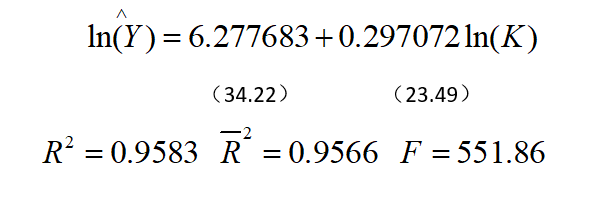
  回归结果表明：$ln(Y)$变化的95.83%可由化肥投入的变化来解释。在0.05的显著性水平下，F统计量的临界值$F_{0.05}(2,23)=3.42<551.86$表明模型的线性关系显著成立。自由度n-k-1=23时，的t检验统计量$t_{0.025}(23)=2.069$，因此$ln(K)$通过0.05显著性水平的显著性检验。

  从$ln(K)$前的参数估计来看，粮食产量关于化肥投入的产出弹性为0.297072，表明当其他因素不变时，化肥投入每增加1%，粮食产量将增加0.297072%，且0<0.297072<1,符合边际报酬递减规律。

7拟合效果及预测效果

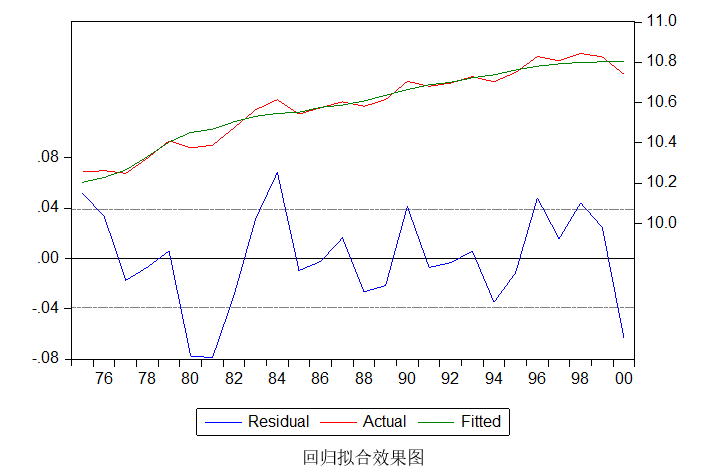
7.1 拟合效果

7.2 预测效果

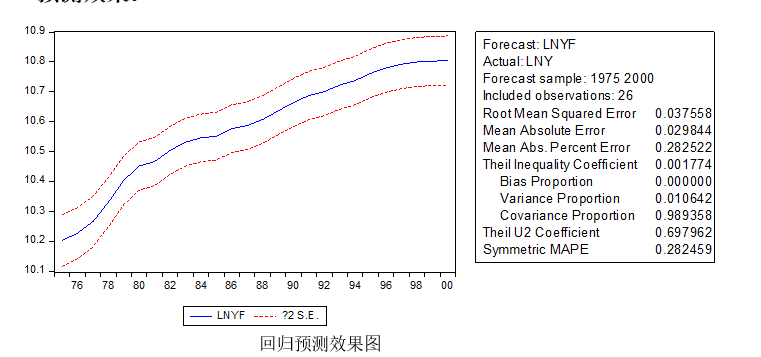
  由回归方程拟合效果、预测效果图可以看出，模型整体拟合效果是较好，且残差在0附近波动，模型建立成功。