1. 决策数模型搭建
1.1 数据预处理
客户违约预测模型的目的是通过已有的客户信息和违约表现来搭建合适的模型，从而预测之后的客户是否会违约。首先通过pandas库读取数据相关知识读取客户的证信数据以及其交易表现，即是否违约记录，代码如下：
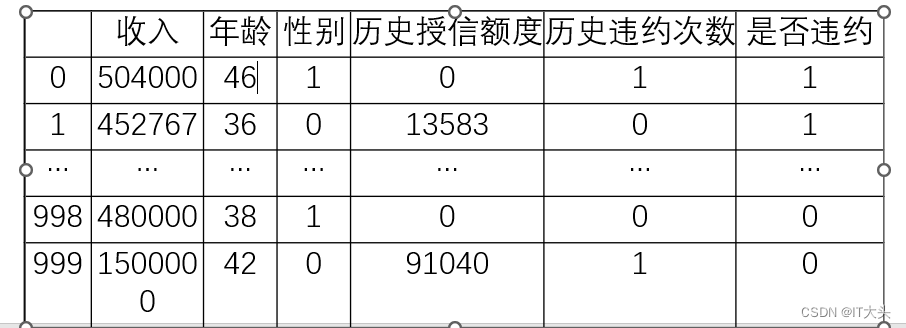
运行结果如下表所示，其中共有1000组历史数据，其中前400个为违约客户数据，后600个为非违约客户数据。因为Python数学建模中无法识别文本内容，所以“性别”及“是否违约”栏中的内容已经进行了数值处理，其中“性别”栏中0表示男，1表示女，“是否违约”栏中0表示不违约，1表示违约。
1.2 特征工程
其中是否违约作为目标变量，剩下的字段作为特征变量，通过一个借款客户的特征来判断他会不会违约。这里为了方便演示，只选取了5个特征变量，在商业实战中，用到的特征变量远比这里的案例多得多。下面便是决策树模型搭建，也是大部分机器学习模型搭建中的常规步骤。
1.2.1 提取特征变量和目标变量
通过如下代码将特征变量和目标变量单独提取出来，代码如下：
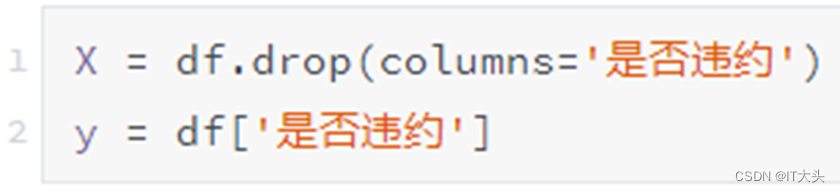
通过drop()函数删除“是否违约”这一列，将剩下的数据作为特征变量赋值给变量X，这里再补充一个删除列的方法：df.drop('是否违约', axis=1)，其中axis=1表示按列进行处理。然后通过DataFrame提取列的方式提取“是否违约”这一列作为目标变量，并赋值给变量y。
1.2.2 划分训练集和测试集
通常我们会根据样本量的大小来划分训练集和测试集，当样本量大的时候，可以划分多一点的比例的数据给训练集，比如有10万组数据的时候，我们可以设定9:1的比例来划分训练集和测试集。这里有1000个数据，并不算多，所以按8:2的比例来划分训练集和测试集。
划分训练集和测试集的代码如下：
因为每次运行程序时，train_test_split()函数都是随机划分数据的，如果想每次划分数据产生的内容都是一致的，可以设置random_state参数，代码如下：
数据的划分是随机的，我们可以将划分后的数据打印出来看下，如下图所示：
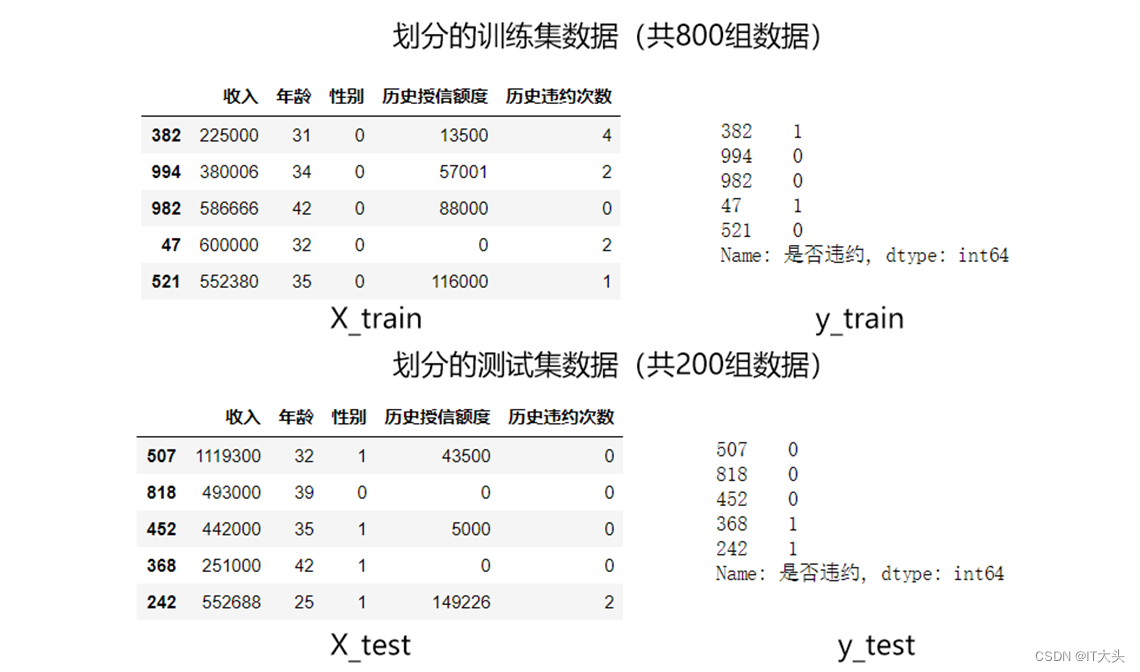
1.3 模型搭建
划分为训练集和测试集之后，就可以从Scikit-Learn库中引入决策树模型进行模型训练了，代码如下：
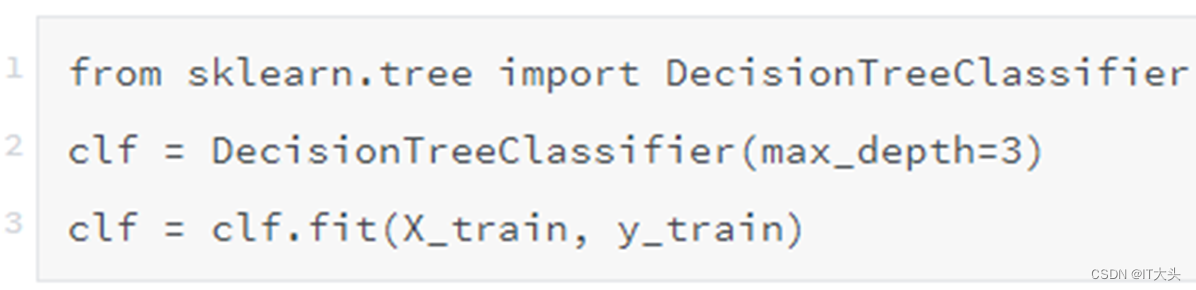
一个决策树模型综合代码：
2. 模型预测与评估
2.1直接预测是否违约
搭建模型的目的便是希望利用它来预测数据，这里把测试集中的数据导入到模型中来进行预测，代码如下，其中clf就是上一节搭建的决策树模型：
预测的y_pred如下图所示，0和1为预测的结果，0为预测会不违约，1为预测会违约。
利用创建DataFrame相关知识点，将预测的y_pred和测试集实际的y_test汇总到一起，其中y_pred是一个numpy.ndarray一维数组结构，y_test为Series一维序列结构，所以这里都用list()函数将其转换为列表，代码如下：
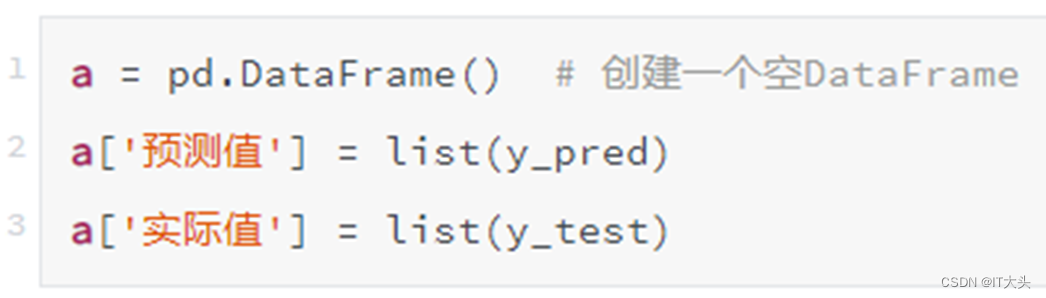
通过print(a.tail())可以将生成的DataFrame后五行打印输出如下：
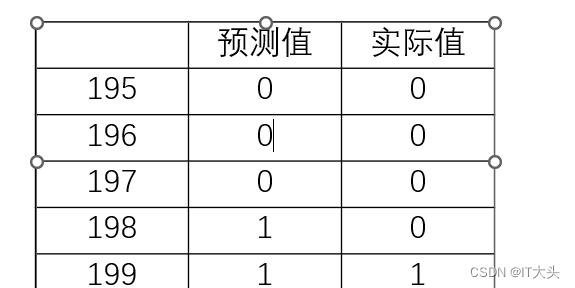
可以看到这里对测试数据集中的全部数据进行了预测，且最后五组数据的预测准确度达到了80%，如果要查看整体的预测准确度，可以采用如下代码：
通过将score打印输出，发现整个模型在测试集上的预测准确度为0.825，即200个测试集数据中，有165人预测结果和实际结果相符。
2.2 预测不违约&违约概率
其实分类决策树模型本质预测的并不是准确的0或1的分类，而是预测其属于某一分类的概率，可以通过如下代码查看预测属于各个分类的概率：
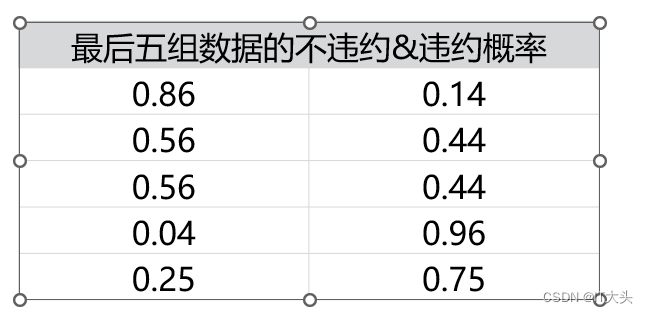
此时获得的y_pred_proba就是预测的属于各个分类的概率，它是一个二维数组，下表展示的便是最后五组数据的不违约&违约概率。
这两个概率的和为1：
二分类问题默认是以0.5作为阈值来预测属于哪一类，因为如果某一类的概率大于0.5，则该类的概率必然大于另一类。实际应用也可以根据需要调节阈值，比如设定只要违约概率大于0.3，就认为该用户会违约。
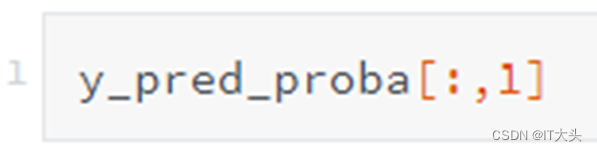
想单纯的查看违约概率，即查看y_pred_proba的第二列，可以采用如下代码：
之前已经利用准确度来衡量了模型的预测效果，不过在商业实战中一般不会以准确度作为模型的评估标准，因为准确度很多时候并不可靠。
举个例子：倘若100个客户里有10个人违约，而如果模型预测所有客户都不会违约，虽然这个模型没有过滤掉一个违约客户，但是模型的预测准确度仍然能达到90%，显然这个较高的准确度并不能反映模型的优劣。
在商业实战中，我们更关心下面两个指标：
其中TP、FP、TN、FN的含义如下表所示，这个表也叫作混淆矩阵：
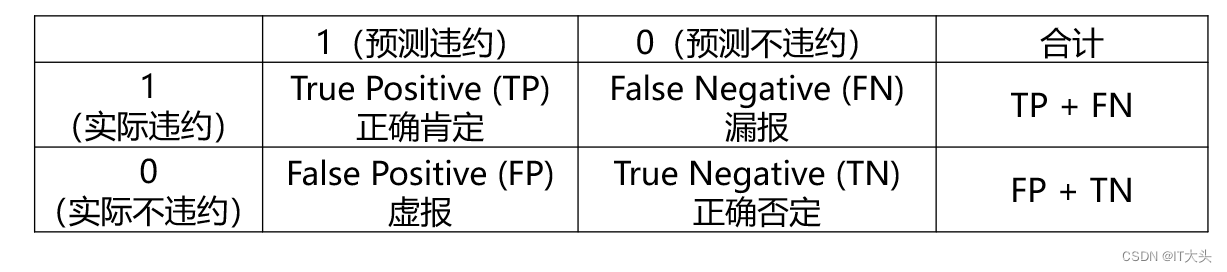
2.3 模型预测效果评估
一个优秀的客户违约预测模型，我们希望命中率（TPR）尽可能的高，即能尽可能地揪出坏人，同时也希望假警报率（FPR）能尽可能的低，即不要误伤好人。
然而这两者往往成正相关性，因为一旦当调高阈值，比如认为违约率超过90%的才认定为违约，那么会导致假警报率很低，但是命中率也很低。
而如果降低阈值的话，比如认为违约率超过10%就认定为违约，那么命中率就会很高，但是假警报率也会很高。
因此为了衡量一个模型的优劣，数据科学家根据不同阈值下的命中率和假警报率绘制了如下的曲线图，称之为ROC曲线：
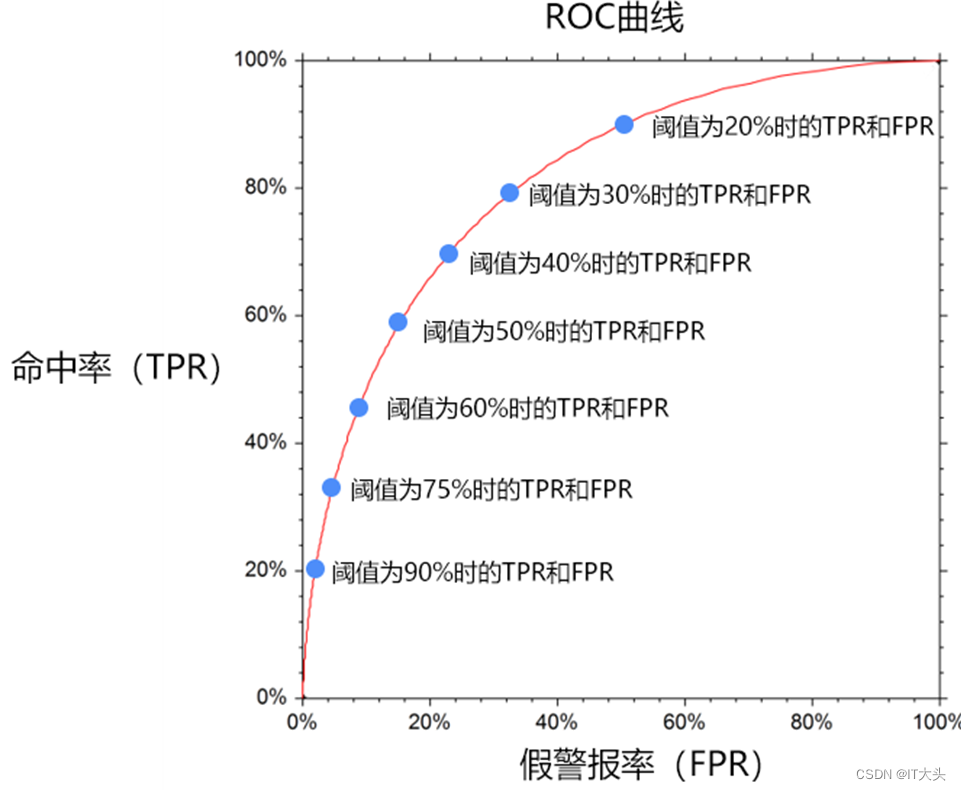
在某一个阈值条件下，我们希望命中率能尽可能的高，而假警报率尽可能的低。
举例来说，某一检测样本总量为100，其中违约客户为20人，当阈值为20%的时候，即违约概率超过20%的时候即认为用户会违约，模型A和模型B预测出来的违约客户都是40人。
模型A预测违约的40人中有20人的确违约，那么命中率达20/20=100%，此时假警报率为20/80=25%。
模型B预测违约的40人中有15人的确违约，那么其命中率为15/20=75%，假警报率为25/80=31.25%。
那么此时认为模型A是一个较优的模型。因此，对于不同模型，我们希望在相同的阈值条件下命中率越高，假警报率越低。
如果把假警报率理解为代价的话，那么命中率就是收益，所以也可以说在相同阈值的情况下，我们希望假警报率（代价）尽量小的情况下，命中率（收益）尽可能的高，该思想反映在图形上也就是这个曲线尽可能的陡峭，曲线越靠近左上角说明在同样的在同样的阈值条件下，命中率越高，假警报率越小，模型越完善。换一个角度来理解，一个完美的模型是在不同的阈值下，假警报率(FPR)则接近于0，而命中率(TPR)都接近于1，该特征反映在图形上，就是曲线非常接近（0，1）这个点，也即曲线非常陡峭。
数值比较上可以使用AUC值来衡量模型的好坏，AUC值（Area Under Curver）指在曲线下面的面积，该面积的取值范围通常为0.5到1，0.5表示随机判断，1则代表完美的模型。
在商业实战中：
AUC值能达到0.75以上就已经可以接受了
如果能达到0.85以上，则为非常不错的模型了
在Python实现上，通过如下代码就可以求出在不同阈值下的假警报率（FPR）以及命中率（TPR）的值，从而可以绘制ROC曲线。
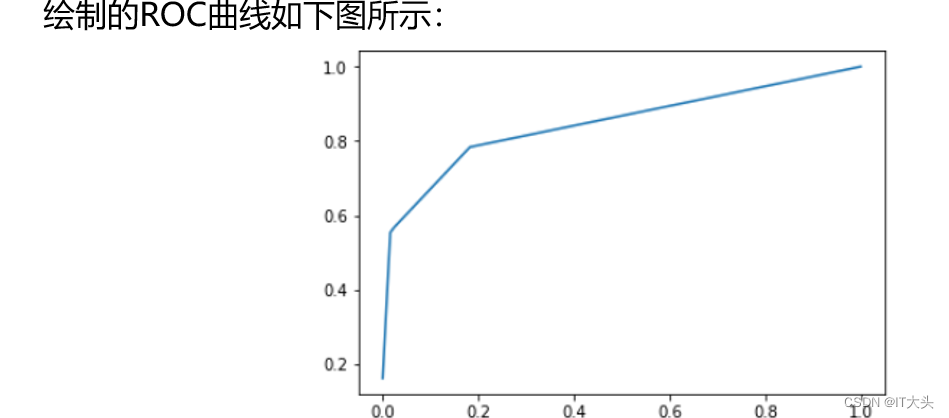
而通过如下代码则可以快速求出模型的AUC值：
其中第一行代码引入roc_auc_score()函数。第二行代码传入测试集目标变量y_test的值，以及预测的违约概率。将获得AUC值打印出来为：0.846，可以说预测效果还是不错的。
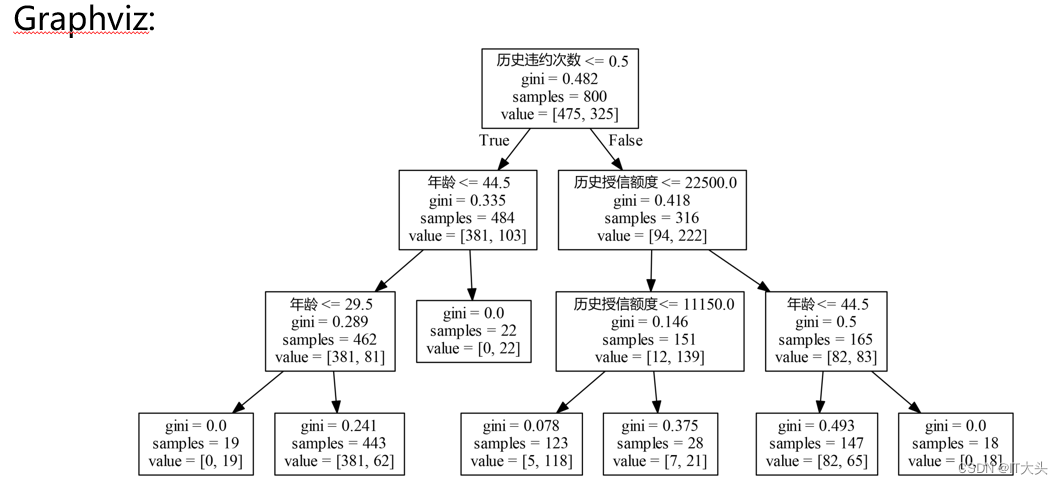
3. 模型可视化呈现
Graphviz:
如果想将决策树模型可视化展示出来，可以使用Python的graphviz插件，下图所示便是上面训练出来的决策树模型。因为模型可视化呈现主要是为了演示和教学，在真正实战中并不怎么会用到，所以对于graphviz的安装与使用，感兴趣的读者可以自行查阅或参考如下网址：https://shimo.im/docs/lUYMJX0TEjoncFZk/
