DFS算法是什么
深度优先搜索算法(Depth First Search 简称DFS算法),一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。
在数据结构中它是属于图的一种遍历算法,从名字我们也可以看出它的遍历方法就是它从一个点开始一直往下遍历直到遍历到空在退回来接着下一个遍历;例如:
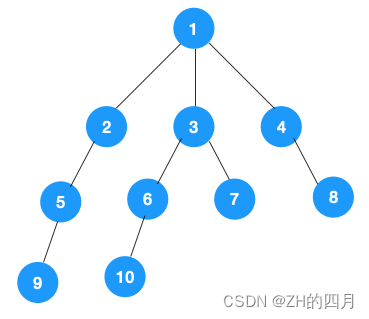
我们用DFS算法去遍历这个图;
从1开始,先遍历2(这里并没有什么要求,也可以先遍历3,但最好是按照顺序去遍历),2遍历之后就开始遍历5,5遍历完之后开始遍历9,9遍历完之后,在往下遍历就是空了,所以就开始往后退,退到5看看5的所有结点遍历完没有,在这里是遍历完了,在往后退到2,看看2左右结点遍历完没有如果遍历完了在退到1,看看1结点遍历完没有,在这里是没有遍历完的就开始去遍历3以此类推
所以它的遍历结果为:
1 2 5 9 3 6 10 7 4 8
这就是深度优先算法
DFS算法模板
c语言模板
int a[510]; //存储每次选出来的数据
int b[510]; //标记是否被访问
int count = 0; //记录符合条件的次数void DFS(int l){if(l == k){ //k个数已经选完,可以进行输出等相关操作 for(int i = 0; i < l; i++){printf("%d ", a[i]);} count++;return ;}for(int i = 0; i < n; i++){ //遍历 n个数,并从中选择k个数 if(!b[i]){ //若没有被访问 b[i] = 1; //标记已被访问 a[l] = i; //选定本数,并加入数组 DFS(l + 1); //递归,l+1 b[i] = 0; //释放,标记为没被访问,方便下次引用 }}
}
我感觉c++的模板可以用类c进行写,我看到一位大佬的博客用的是vector容器
大佬的博客为:DFS (深度优先搜索) 算法详解 + 模板 + 例题,这一篇就够了_dfs算法-CSDN博客
c++模板
vector<int> a; // 记录每次排列
vector<int> book; //标记是否被访问 void DFS(int cur, int k, vector<int>& nums){if(cur == k){ //k个数已经选完,可以进行输出等相关操作 for(int i = 0; i < cur; i++){printf("%d ", a[i]);} return ;}for(int i = 0; i < k; i++){ //遍历 n个数,并从中选择k个数 if(book[nums[i]] == 0){ //若没有被访问a.push_back(nums[i]); //选定本输,并加入数组 book[nums[i]] = 1; //标记已被访问 DFS(cur + 1, n, nums); //递归,cur+1 book[nums[i]] = 0; //释放,标记为没被访问,方便下次引用 a.pop_back(); //弹出刚刚标记为未访问的数}}
}
题例
多说无益以题见真章
P8707 [蓝桥杯 2020 省 AB1] 走方格
题目
题目描述:
在平面上有一些二维的点阵。
这些点的编号就像二维数组的编号一样,从上到下依次为第 11 至第 nn 行,从左到右依次为第 11 至第 mm 列,每一个点可以用行号和列号来表示。
现在有个人站在第 11 行第 11 列,要走到第 nn 行第 mm 列。只能向右或者向下走。
注意,如果行号和列数都是偶数,不能走入这一格中。
问有多少种方案。
输入格式:
输入一行包含两个整数 nn,mm。
输出格式:
输出一个整数,表示答案。
输入样例
3 4输出样例
2题目地址:[蓝桥杯 2020 省 AB1] 走方格 - 洛谷
这道题感觉就是走迷宫的简便版
先附上代码
#include <bits/extc++.h>
#define int long longusing namespace std;int n,m;int dfs(int x,int y){if(x>n||y>m) //如果越界了,那么就不算.return 0; if(x==n&&y==m) 走到第 n 行第 m 列时,证明我们已经走到了终点,所以增加 1 .return 1;if((x%2==0)&&(y%2==0)) //如果走到了题目中规定不走的格子,那么也不算.return 0; //注意if的顺序不能错哟int ans=dfs(x+1,y)+dfs(x,y+1); //递归求解return ans; //返回答案
}signed main(){cin>>n>>m;cout<<dfs(1,1);
}这个你提交上去它会提示你最后一步超时了,这是为什么呢?这就是递归的弊端了;
在这里它每次都会有两次选择要么向下走,要么向右走,这里不用考虑向上,向左走,因为你已经在左上端了,向右和向下就可以到达目的地了,所以当n和m的值特别大,时间复杂度就是指数级别的
接下来就是第二种方法,进行记录,先上代码
#include <bits/stdc++.h>using namespace std;int n,m;
int mem[100][100]; //记忆化int dfs(int x,int y){if(x>n||y>m)return 0;if(x==n&&y==m)return 1;if((x%2==0)&&(y%2==0))return 0;if(mem[x][y]!=-1)return mem[x][y];int ans=dfs(x+1,y)+dfs(x,y+1);return mem[x][y]=ans;
}signed main(){memset(mem,-1,sizeof(mem)); //记得清空为-1cin>>n>>m;cout<<dfs(1,1);
}这次多加了一个数组进行记录如果遍历到就将这个数记录下来,下一次如果遇到相同的直接返回值就行;这次时间复杂度就为O(m*n)每走一步就记录下来那么每个函数就只访问一次
交上去是正确的
P8662 [蓝桥杯 2018 省 AB] 全球变暖
题目
题目描述:
# [蓝桥杯 2018 省 AB] 全球变暖
## 题目描述
你有一张某海域 $N \times N$ 像素的照片,`.` 表示海洋、 `#` 表示陆地,如下所示:
```
.......
.##....
.##....
....##.
..####.
...###.
.......
```
其中 "上下左右" 四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 $2$ 座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
```
.......
.......
.......
.......
....#..
.......
.......
```
请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
## 输入格式
第一行包含一个整数 $N$。$(1 \le N \le 1000)$。
以下 $N$ 行 $N$ 列代表一张海域照片。
照片保证第 $1$ 行、第 $1$ 列、第 $N$ 行、第 $N$ 列的像素都是海洋。
## 输出格式
一个整数表示答案。
## 样例 #1
### 样例输入 #1
```
7
.......
.##....
.##....
....##.
..####.
...###.
.......
```
### 样例输出 #1
```
1
```
## 提示
时限 1 秒, 256M。蓝桥杯 2018 年第九届省赛
题目链接:[蓝桥杯 2018 省 AB] 全球变暖 - 洛谷
先上代码
#include<bits/stdc++.h>
using namespace std;
int n,cnt,sum,ans,t,dx[]={0,1,0,-1},dy[]={1,0,-1,0}; //dx,dy表示四个方向
char mp[1010][1010];
void dfs(int x,int y)
{if(!t){cnt=0;for(int i=0;i<4;i++){if(mp[x+dx[i]][y+dy[i]]!='.'){cnt++;}} //记录它四个方向是不是陆地if(cnt==4)ans++,t=1; //如果四个方向都是陆地那么它就不会被淹没}mp[x][y]='*';for(int i=0;i<4;i++){int xx=x+dx[i],yy=y+dy[i]; if(xx<0||xx>=n||yy<0||yy>=n||mp[xx][yy]!='#')continue;dfs(xx,yy);} //这个是检查它的越界问题并且进行递归
}
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>mp[i][j];}} for(int i=1;i<n-1;i++){for(int j=1;j<n-1;j++){if(mp[i][j]=='#'){sum++;t=0;dfs(i,j);}}}cout<<sum-ans;
}解释一下这段代码的大概含义,就是设置一个主函数并且用t进行记录,从而不让他重复记录小岛,如果t=0说明这个陆地还没有被记录,如果t=1说明这个小岛已经被记录了,它的上下左右的一个陆地已经被记录代表这个小岛了,直到将这个小岛的全部陆地全部记录完在进行返回主函数进行下一次的循环;
在学这个算法时候发现自己的递归没有学好,一些小的细节没有搞懂,之后在思考思考,之后会在发文章进行补充;