【小白学机器学习8】统计里的自由度DF=degree of freedom, 以及关于df=n-k， df=n-k-1, df=n-1 等自由度公式-编程知识

1 自由度 /degree of freedom / df

1.1 物理学的自由度

1.2 数学里的自由度

1.2.1 数学里的自由度

1.2.2 用线性代数来理解自由度（需要补充）

1.2.3 统计里的自由度

1.3 统计学里自由度的定义

2 不同对象的自由度

2.1 纯公式的自由度：纯公式，没采样无样本时

2.2 抽样分析时：纯样本的自由度

2.3 公式里某个特定变量的自由度

3 自由度的公式

3.1 自由度的基础公式 df=n-k

3.2 ESS 残差平方和的误差 df=n-k-1

3.3 回归方程的自由度, df=n-k-1=n-1

3.3.1 一元线性回归

3.3.2 多元线性回归

4 参考

5 其他（未完成）

1 自由度 /degree of freedom / df

1.1 物理学的自由度

理论力学：（下面这段摘自网上）

确定物体的位置所需要的独立坐标数称作物体的自由度，当物体受到某些限制时——自由度减少。
一个质点在空间自由运动，它的位置由三个独立坐标就可以确定，所以质点的运动有三个自由度。
假如将质点限制在一个平面或一个曲面上运动，它有两个自由度。
假如将质点限制在一条直线或一条曲线上运动，它只有一个自由度。
刚体在空间的运动既有平动也有转动，其自由度有六个，即三个平动自由度x、y、z和三个转动自由度a、b、q。如果刚体运动存在某些限制条件，自由度会相应减少。

1.2 数学里的自由度

1.2.1 数学里的自由度

数学上，自由度是一个随机向量的维度数
也就是一个向量能被完整描述所需的最少单位向量数

1.2.2 用线性代数来理解自由度（需要补充）

从线性代数的角度理解
自由度就是向量/矩阵/张量的维度，秩。最少需要用几个维度来现实就是自由度.

1.2.3 统计里的自由度

样本容量越大，自由度就越高，就越趋近于正态分布，实验就更加合理
下图时转载的，文章链接附在最后

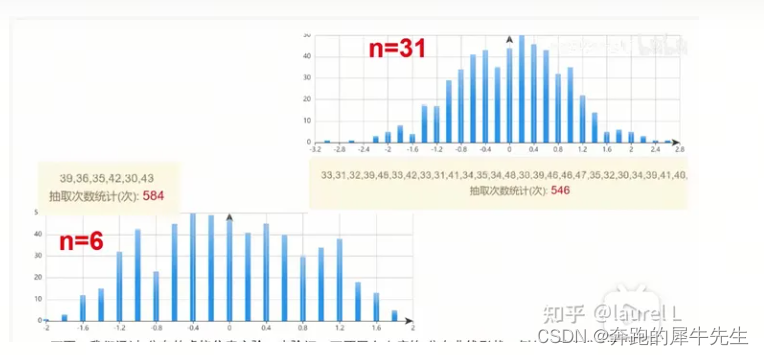
1.3 统计学里自由度的定义

自由度通常用于抽样分布中。

统计学中：在统计模型中，自由度指样本中可以自由变动的独立不相关的变量的个数，当有约束条件时，自由度减少。

样本中独立或能自由变化的数据的个数，称为该统计量的自由度。
自由度指的是计算某一统计量时，取值不受限制的变量个数。

2 不同对象的自由度

通用的自由度公式，都是n-k。但是不同对象下的DF的意义不同
- 如果讲的是公式的自由度，是自变量的个数 df=n
- 如果讲的是样本的自由度，是样本的数量减去约束条件个数，df=n-k
- 如果讲的是某个公式里某个特定变量的自由度，是样本的数量减去约束条件个数，df=n-k

2.1 纯公式的自由度：纯公式，没采样无样本时

抽象的公式的自由度：不受约束自变量的个数
不受约束的自变量个数就是公式的自由度。

举例：

一元线性回归：y=ax+b
x是自变量，自由度1
y是因变量，没有自由度
总自由度1
多元线性回归：y=a1X1+a2X2+......anXn
x是自变量，自由度n
y是因变量，没有自由度
总自由度n

2.2 抽样分析时：纯样本的自由度

样本的自由度=n-k
样本数量n
关于样本的约束条件k，比如用到了样本的均值，就少1个自由度

举例

a+b=1，其中a,b都是变量，那么总自由度为1，因为若a为变量，b会受到1-a的约束，所以不自由。自由度=2个自变量-1被限制的自变量=1
总体平均数,u=average(x)。因为总体内，每个样本都是独立的，所以自由度就是总体的容量n
样本平均数，average(xi) ，假设有10个样本，平均数=1，那只有前9个数可以自由取值，第10个数，一定得受到平均值得约束，因此自由度=n-1=10-1=9
总体方差，公式为
样本方差，公式为,因为本身是一个样本的约束，所以自由度=n-1

2.3 公式里某个特定变量的自由度

如果讲的是公式里某个特定变量的自由度，是样本的数量减去约束条件个数，df=n-k
通用的公式都是这个，df=n-k
但是还可以细分，下面详细展开

3 自由度的公式

3.1 自由度的基础公式 df=n-k

自由度计算公式：自由度=样本个数-样本数据受约束条件的个数，即df = n - k（df自由度，n样本个数，k约束条件个数）

df=n-k。
自由度df：
- 不受限制的变量个数
- 不受限制的样本个数
n：
- 自变量个数
- 样本数量
k：
- 被限制的条件数或变量个数
- 或计算某一统计量时用到其它独立统计量的个数。
- 这些变量之间的有公式关系等形成的约束个数（应该要减掉一些线性相关的约束）

3.2 ESS 残差平方和的误差 df=n-k-1 （比n-k多出的-1是指那个截距参数）

需要考虑2方面
模型中自变量的个数，+自由度
模型中有几个未知数就要消耗几个自由度，-自由度

举例

观测值y
预测值y^
一元线性回归模型 y＝b0＋b1X＋ε，因为每个y^都是用这个模型估算出来的
y^-y的误差就是残差，也就是ε
b0 常数，截距
b1 自变量x的参数，未知，需要求
ε 残差，残差的均值=0

另外，我们心中有一个理想模型y＝b0＋b1X （虽然不一定存在，不能能找到），但是我们相信我们的观测值符合一个这样的理想直线模型（否则我们也不会用线性回归，而是用曲线或者其他了^ ^）
y^观测值,记录下来
理想模型的y观测值：y=b0+b1X
ESS=Σ(y^-y)**2 =Σ(y^-b0+b1X)**2

残差平方和 ESS 的自由度
残差平方和 ESS=Σ(y^-y)**2，因为因为每个y^=b0＋b1X，包含2个参数b0,b1 因此需要确定这2个参数，就需要2个约束才能算出来
为什么2个参数需要2个约束：因为解方程的需要，而且这2个约束还不能是线性相关的才行。因此有几个未知参数就消耗几个自由度
所以:
一元线性回归的ESS的自由度df = n-k-1=n-1-1=n-2
多元线性回归的ESS的自由度 df =n-k-1
其中k 是变量个数，1是截距常量个数。

3.3 回归方程的自由度, df=n-k-1=n-1

3.3.1 一元线性回归

回归方程 y＝b0＋b1X
其中自变量X，只有1个，自由度+1
而参数是2个，也就是2个未知数，b0 和b1，自由度-2
如果有n个样本
那么回归方程的自由度= n-2+1=n-1

3.3.2 多元线性回归

回归方程 y＝b0＋b1X+b2X+....+bkX，
其中自变量X，有k个自变量，自由度+k
而参数是k+1个，所有x的参数，还一个一个截距。这些都是未知数。
如果有n个样本
那么回归方程的自由度= n+k-(k+1)=n-1

4 参考

【弱鸡版】什么回归中自由度（degrees of freedom），就是这么简单！ - 知乎自由度是什么？我们先来百度一下： “自由度(degree of freedom, df)指的是计算某一统计量时，取值不受限制的变量个数。通常df=n-k。其中n为样本数量，k为被限制的条件数或变量个数，或计算某一统计量时用到其它…https://zhuanlan.zhihu.com/p/607458488

一元线性回归模型中残差平方和的自由度为什么是n-2 - 爱问频道 - 经管之家(原人大经济论坛)一元线性回归模型中残差平方和的自由度为什么是n-2,一元线性回归模型中残差平方和的自由度为什么是n-2？,经管之家(原人大经济论坛)https://bbs.pinggu.org/thread-640905-1-1.html

下面这个解释了多种DF的定义，可惜我还没仔细看~~

统计学“自由度”详解 - 知乎本文皆为个人看法，才疏学浅，如果有不妥不准确的对方，还请指正。有些数学推导可能显得不严谨，主要是为了数学基础薄弱的同学能看懂。 “自由度”是统计学中一个很不好懂的概念，因为它的定义有好几个，而每个定…https://zhuanlan.zhihu.com/p/81099139