机器学习-04-分类算法-03KNN算法-编程知识

总结

本系列是机器学习课程的系列课程，主要介绍机器学习中分类算法，本篇为分类算法与knn算法部分。

本门课程的目标

完成一个特定行业的算法应用全过程：

懂业务+会选择合适的算法+数据处理+算法训练+算法调优+算法融合
+算法评估+持续调优+工程化接口实现

参考

KNN算法（k近邻算法）原理及总结
图解机器学习 | KNN算法及其应用

数据科学中常见的9种距离度量方法，内含欧氏距离、切比雪夫距离等

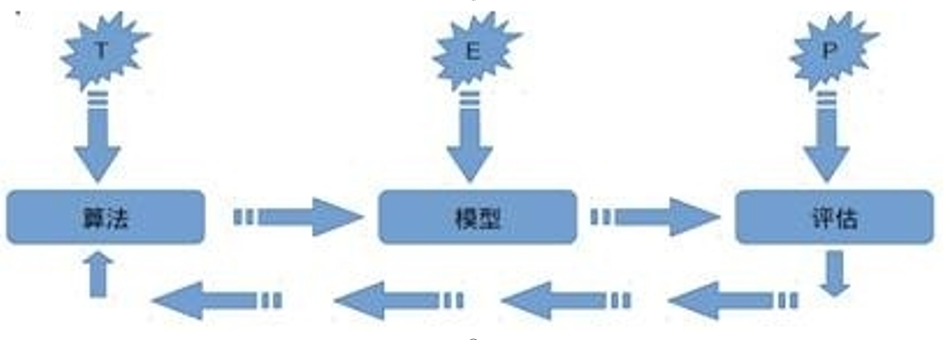
机器学习定义

关于机器学习的定义，Tom Michael Mitchell的这段话被广泛引用：
对于某类任务T和性能度量P，如果一个计算机程序在T上其性能P随着经验E而自我完善，那么我们称这个计算机程序从经验E中学习。

KNN算法

分类问题

分类问题是机器学习非常重要的一个组成部分，它的目标是根据已知样本的某些特征，判断一个样本属于哪个类别。分类问题可以细分如下：
在这里插入图片描述

二分类问题：表示分类任务中有两个类别新的样本属于哪种已知的样本类。
多类分类（Multiclass classification）问题：表示分类任务中有多类别。
多标签分类（Multilabel classification）问题：给每个样本一系列的目标标签。

分类问题的数学抽象
从算法的角度解决一个分类问题，我们的训练数据会被映射成n维空间的样本点（这里的n就是特征维度），我们需要做的事情是对n维样本空间的点进行类别区分，某些点会归属到某个类别。

下图所示的是二维平面中的两类样本点，我们的模型（分类器）在学习一种区分不同类别的方法，比如这里是使用一条直线去对两类不同的样本点进行切分。
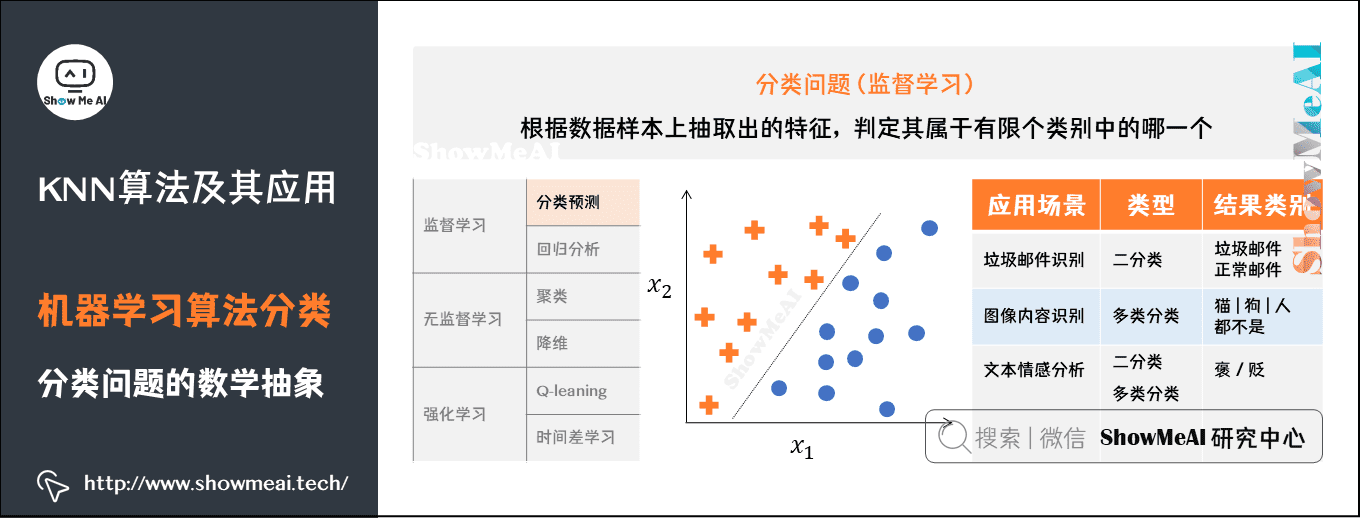
在这里插入图片描述

常见的分类问题应用场景很多，我们选择几个进行举例说明：

垃圾邮件识别：可以作为二分类问题，将邮件分为你「垃圾邮件」或者「正常邮件」。
图像内容识别：因为图像的内容种类不止一个，图像内容可能是猫、狗、人等等，因此是多类分类问题。
文本情感分析：既可以作为二分类问题，将情感分为褒贬两种，还可以作为多类分类问题，将情感种类扩展，比如分为：十分消极、消极、积极、十分积极等。

KNN简介

近邻算法（K-nearest neighbors，KNN ，有些地方也译作「近邻算法」）是一种很基本朴实的机器学习方法。

KNN 在我们日常生活中也有类似的思想应用，比如，我们判断一个人的人品，往往只需要观察他最密切的几个人的人品好坏就能得到结果了。这就是 KNN 的思想应用，KNN 方法既可以做分类，也可以做回归。

在模式识别领域中，近邻算法（ KNN 算法，又译最近邻算法）是一种用于分类和回归的非参数统计方法。在这两种情况下，输入包含特征空间中的个最接近的训练样本。

1）K近邻核心思想
在 KNN 分类中，输出是一个分类族群。一个对象的分类是由其邻居的「多数表决」确定的，K个最近邻居（K为正整数，通常较小）中最常见的分类决定了赋予该对象的类别。

若K=1，则该对象的类别直接由最近的一个节点赋予。
在 KNN 回归中，输出是该对象的属性值。该值是其K个最近邻居的值的平均值。
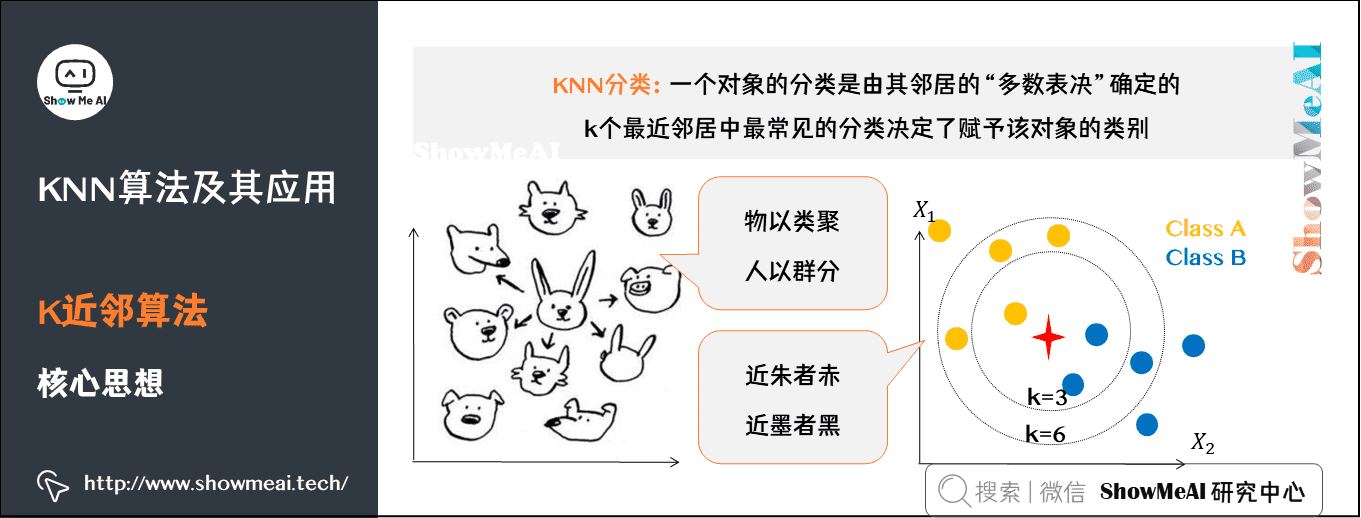
在这里插入图片描述

K近邻居法采用向量空间模型来分类，概念为相同类别的案例，彼此的相似度高。而可以借由计算与已知类别案例之相似度，来评估未知类别案例可能的分类。

KNN 是一种基于实例的学习，或者是局部近似和将所有计算推迟到分类之后的惰性学习。近邻算法是所有的机器学习算法中最简单的之一。

KNN思想

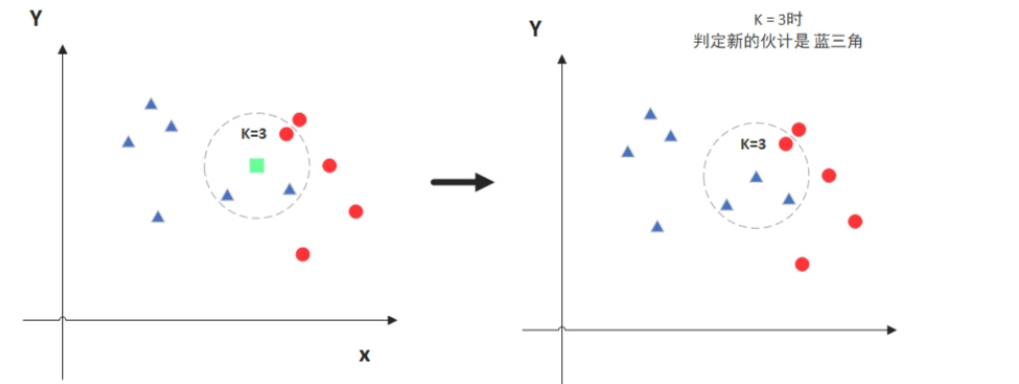
在这里插入图片描述

图中绿色的点就是我们要预测的那个点，假设K=3。那么KNN算法就会找到与它距离最近的三个点（这里用圆圈把它圈起来了），看看哪种类别多一些，比如这个例子中是蓝色三角形多一些，新来的绿色点就归类到蓝三角了。

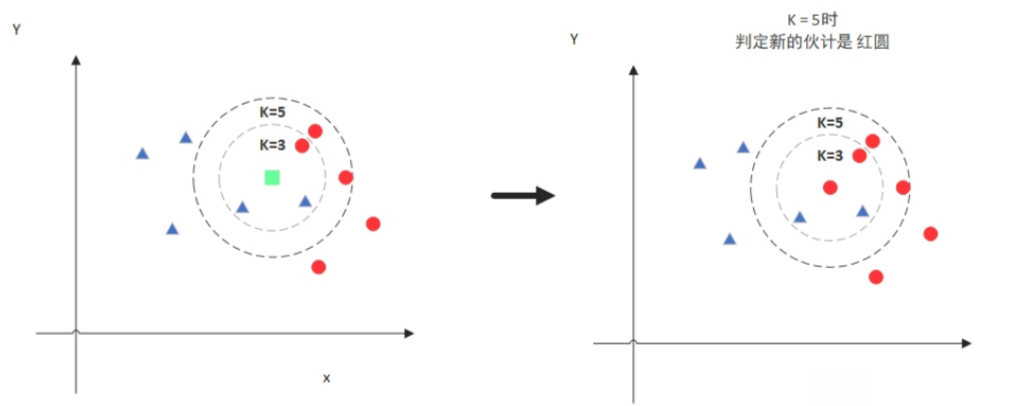
在这里插入图片描述

但是，当K=5的时候，判定就变成不一样了。这次变成红圆多一些，所以新来的绿点被归类成红圆。从这个例子中，我们就能看得出K的取值是很重要的。
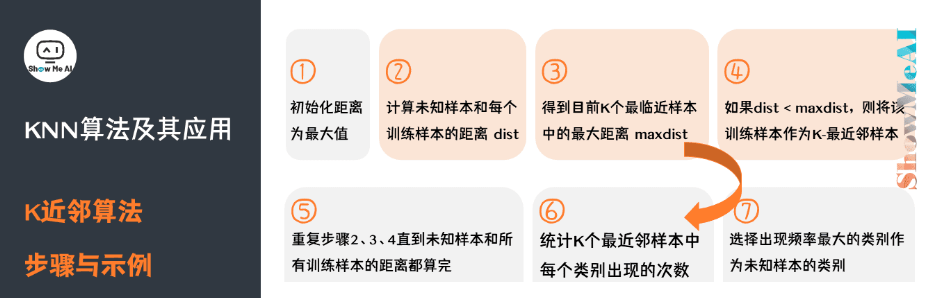
在这里插入图片描述

K值的选取

我们可以通过交叉验证获得较好的k值，开始选取一个较小的K值，不断增加K值，然后计算验证集合的方差，最终找到一个比较合适的K值。如下图：
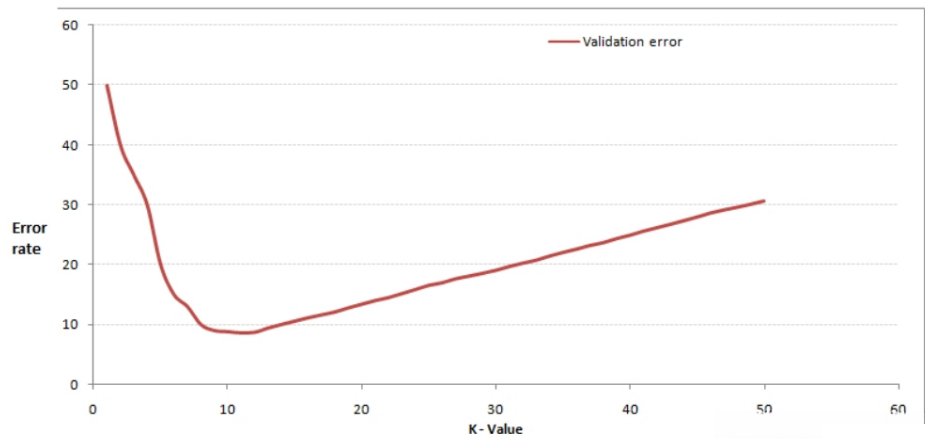
在这里插入图片描述

增大k的时候，一般错误率会先降低，因为有周围更多的样本可以借鉴了，分类效果会变好。当K值更大的时候，错误率会更高。比如说你一共就35个样本，当你K增大到30的时候，KNN基本上就没意义了。

所以选择K点的时候可以选择一个较大的临界K点，当它继续增大或减小的时候，错误率都会上升，比如图中的K=10。

点距离的计算

欧式距离

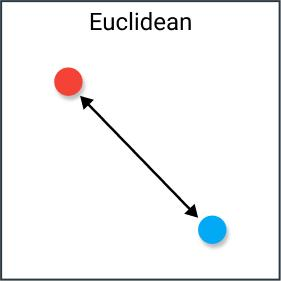
在这里插入图片描述

欧几里得距离：它也被称为L2范数距离。欧几里得距离是我们在平面几何中最常用的距离计算方法，即两点之间的直线距离。在n维空间中，两点之间的欧几里得距离计算公式为：
在这里插入图片描述

def euclidean_distance(x1, x2): return math.sqrt(np.sum((x1 - x2)**2))

euclidean_distance函数计算多维空间中两点(x1和x2)之间的欧氏距离，函数的工作原理如下:

从x1元素中减去x2，得到对应坐标之间的差值。
使用**2运算将差值平方。
使用np.sum()对差的平方求和。
使用math.sqrt()取总和的平方根。
欧几里得距离是欧几里得空间中两点之间的直线距离。通过计算欧几里得距离，可以识别给定样本的最近邻居，并根据邻居的多数类(用于分类)或平均值(用于回归)进行预测。在处理连续的实值特征时，使用欧几里得距离很有帮助，因为它提供了一种直观的相似性度量。

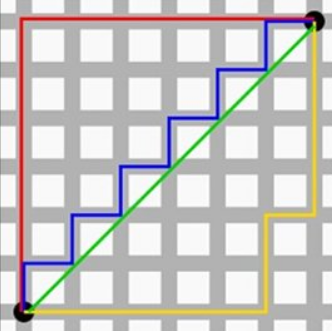
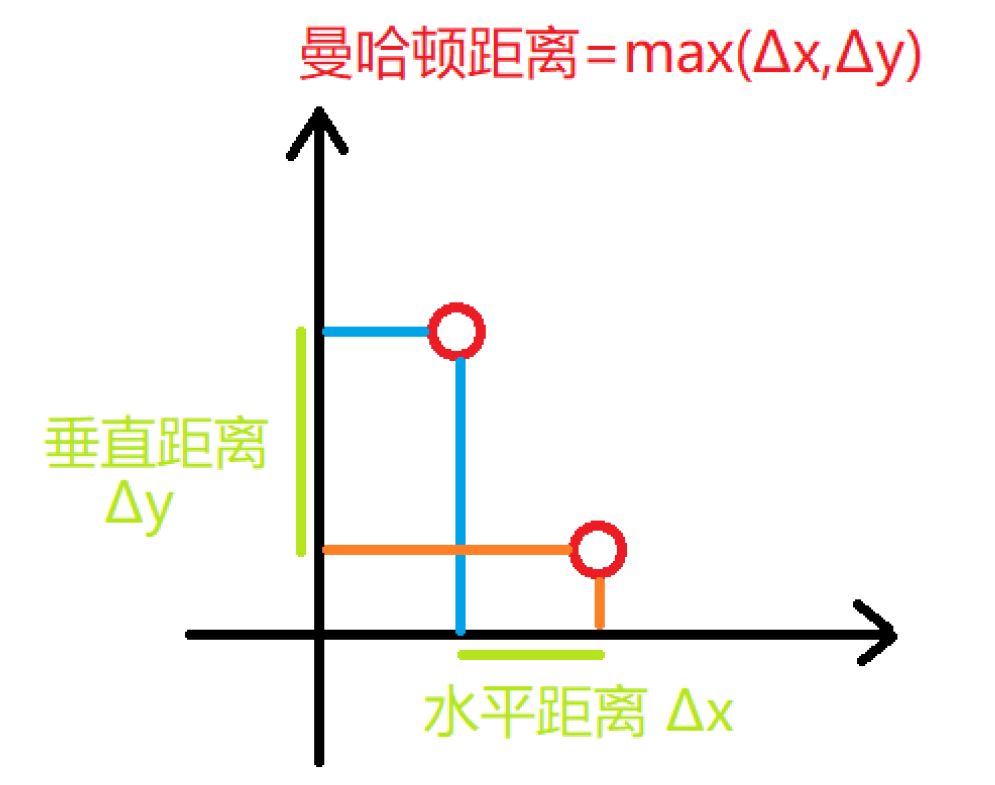
曼哈顿距离

KNN算法通常的距离测算方式为欧式距离和曼哈顿距离。
在这里插入图片描述

在这里插入图片描述

KNN 优缺点

KNN算法优点

简单易用，相比其他算法，KNN算是比较简洁明了的算法。即使没有很高的数学基础也能搞清楚它的原理。
模型训练时间快，上面说到KNN算法是惰性的，这里也就不再过多讲述。
预测效果好。
对异常值不敏感

KNN算法缺点

对内存要求较高，因为该算法存储了所有训练数据
值的确定： KNN 算法必须指定K 值，K值选择不当则分类精度不能保证。
预测阶段可能很慢
对不相关的功能和数据规模敏感

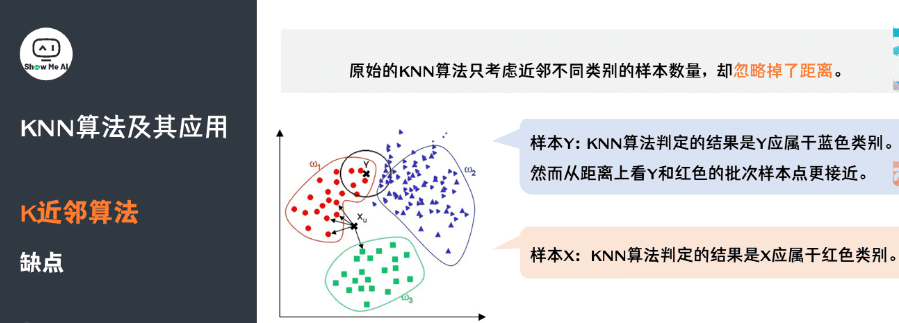
观察下面的例子，我们看到，对于样本，通过 KNN 算法，我们显然可以得到Y应属于红色类别。但对于样本，KNN 算法判定的结果是Y 应属于蓝色类别，然而从距离上看Y和红色的批次样本点更接近。因此，原始的 KNN 算法只考虑近邻不同类别的样本数量，而忽略掉了距离。
在这里插入图片描述

KNN过程

KNN分类器算法
1）计算测试数据与各个训练数据之间的距离；
2）按照距离的递增关系进行排序；
3）选取距离最小的K个点；
4）确定前K个点所在类别的出现频率；
5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

K近邻算法的一般流程

数据准备：这包括收集、清洗和预处理数据。预处理可能包括归一化或标准化特征，以确保所有特征在计算距离时具有相等的权重。

玩视频游戏所耗时间百分比	每年获得的飞行常客里程数	每周消费的冰淇淋的公升数	样本分类
1	0.8	400	0.5
2	12	134000	0.9
3	0	20000	1.1
4	67	32000	0.1

我们很容易发现，当计算样本之间的距离时数字差值最大的属性对计算结果的影响最大，也就是说，每年获取的飞行常客里程数对于计算结果的影响将远远大于上表中其他两个特征-玩视频游戏所耗时间占比和每周消费冰淇淋公斤数的影响。而产生这种现象的唯一原因，仅仅是因为飞行常客里程数远大于其他特征值。但海伦认为这三种特征是同等重要的，因此作为三个等权重的特征之一，飞行常客里程数并不应该如此严重地影响到计算结果。

在处理这种不同取值范围的特征值时，我们通常采用的方法是将数值归一化，如将取值范围处理为０到１或者-１到１之间。下面的公式可以将任意取值范围的特征值转化为０到１区间内的值：

选择距离度量方法：
确定用于比较样本之间相似性的度量方法，常见的如欧几里得距离、曼哈顿距离等。

确定K值：
选择一个K值，即在分类或回归时应考虑的邻居数量。这是一个超参数，可以通过交叉验证等方法来选择最优的K值。

找到K个最近邻居：
对于每一个需要预测的未标记的样本：
计算该样本与训练集中所有样本的距离。
根据距离对它们进行排序。
选择距离最近的K个样本

预测：
对于分类任务：查看K个最近邻居中最常见的类别，作为预测结果。例如，如果K=3，并且三个最近邻居的类别是[1, 2, 1]，那么预测结果就是类别1。
对于回归任务：预测结果可以是K个最近邻居的平均值或加权平均值。

评估：
使用适当的评价指标（如准确率、均方误差等）评估模型的性能。

优化：
基于性能评估结果，可能需要返回并调整某些参数，如K值、距离度量方法等，以获得更好的性能。

sklearn中的knn

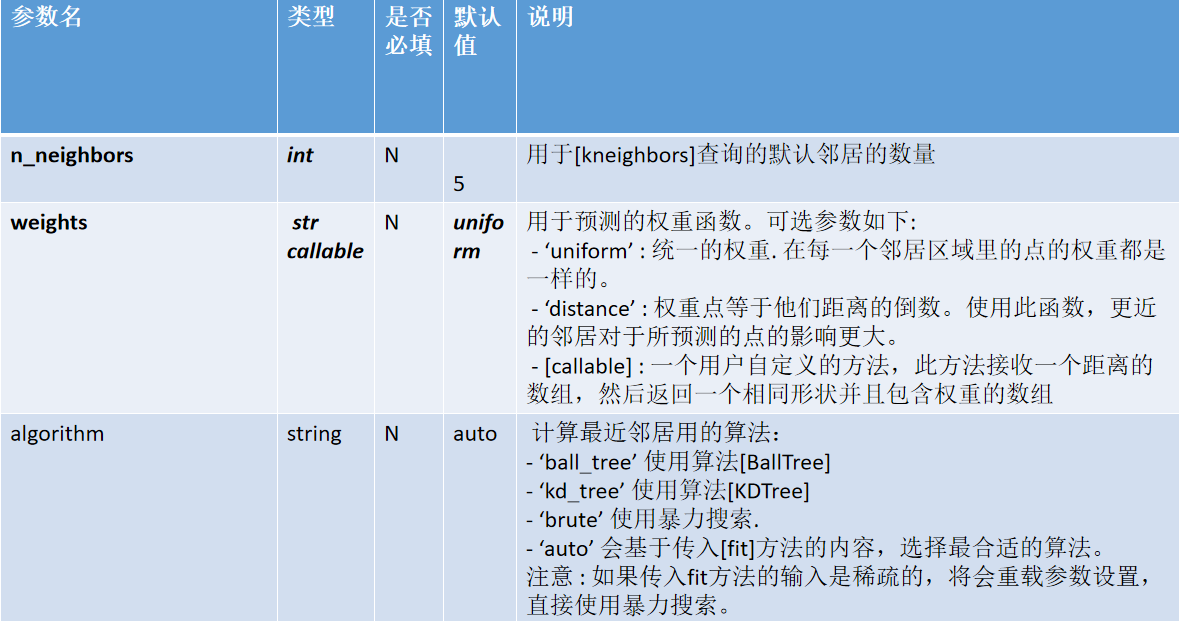
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=None, **kwargs)

参考：官网链接

在这里插入图片描述

案例1

#加载数据
from sklearn import datasets
iris = datasets.load_iris()
#导入模型
from sklearn.neighbors import KNeighborsClassifier 
knn = KNeighborsClassifier()
#训练模型+预测数据
y_pred = knn.fit(iris.data, iris.target).predict(iris.data)
##输出
print("Number of mislabeled points out of a total %d points : %d"% (iris.data.shape[0],(iris.target != y_pred).sum()))

输出为：
Number of mislabeled points out of a total 150 points : 5

案例2

#加载数据
from sklearn import datasets
from sklearn.model_selection import GridSearchCV, train_test_split
#导入模型
from sklearn.neighbors import KNeighborsClassifier
iris = datasets.load_iris()
train_x,test_x,train_y,test_y=train_test_split(iris.data,iris.target)
knn = KNeighborsClassifier()
#超参数配置
param_knn = {
'n_neighbors': list(range(3,15,2)),
'algorithm':['auto', 'ball_tree', 'kd_tree', 'brute'],
‘p':list(range(1,2))
}
#KNN的超参数
gsearch_knn = GridSearchCV( knn , param_grid = param_knn, cv=10 )
gsearch_knn.fit( train_x, train_y )
gsearch_knn.best_params_
gsearch_knn.best_score_
best_knn=gsearch_knn.best_estimator_
#训练模型+预测数据
y_pred = best_knn.predict(test_x)
y_pred

输出为：
array([2, 2, 0, 1, 2, 2, 2, 1, 0, 0, 1, 1, 2, 1, 2, 0, 2, 2, 0, 1, 2, 1,
2, 0, 2, 2, 0, 0, 2, 2, 0, 1, 2, 0, 0, 1, 0, 0])

from sklearn.metrics import accuracy_score
accuracy_score(test_y, y_pred)

输出为：
0.9473684210526315

案例3-手写实现

#导入所需要的包
import numpy as np
from math import sqrt
from collections import Counter
#定义knn函数
def knn_distance(k, X_train, Y_train, x):#保证K有效assert 1 <= k <= X_train.shape[0], "K must be valid"#X_train的值必须等于y_train的值assert X_train.shape[0] == Y_train.shape[0], "the size of X_train must equal to the size of y_train"#x的特征号必须等于X_trainassert X_train.shape[1] == x.shape[0], "the feature number of x must be equal to X_train"#迅速计算距离distance = [sqrt(np.sum((x_train - x)**2)) for x_train in X_train]#返回距离值从小到大排序后的索引值的数组nearest = np.argsort(distance)#获取距离最小的前k个样本的标签topk_y = [Y_train[i] for i in nearest[:k]]#统计前k个样本的标签类别以及对应的频数votes = Counter(topk_y)#返回频数最多的类别return votes.most_common(1)[0][0]
if __name__ == "__main__":#使用numpy生成8个点X_train = np.array([[1.0, 3.5],[2.0, 7],[3.0, 10.5],[4.0, 14],[5, 25],[6, 30],[7, 35],[8, 40]])#使用numpy生成8个点对应的类别Y_train = np.array([0, 0, 0, 0, 1, 1, 1, 1])#使用numpy生成待分类样本点x = np.array([8, 21])#调用distance函数并传入参数label = knn_distance(3, X_train, Y_train, x)#显示待测样本点的分类结果print(label)