再了解堆之前我们先要了解树和二叉树的基本知识
可以看我的上一篇文章

堆

• 堆逻辑结构是完全二叉树，但堆一般用顺序表存储
• 堆只有大堆（大顶堆）和小堆（小顶堆）
  大堆：左右孩子节点中存储的数据都必须小于等于父亲节点，根节点最大
  小堆：左右孩子节点中存储的数据都必须大于等于父亲节点，根节点最小

堆的顺序存储

如下图

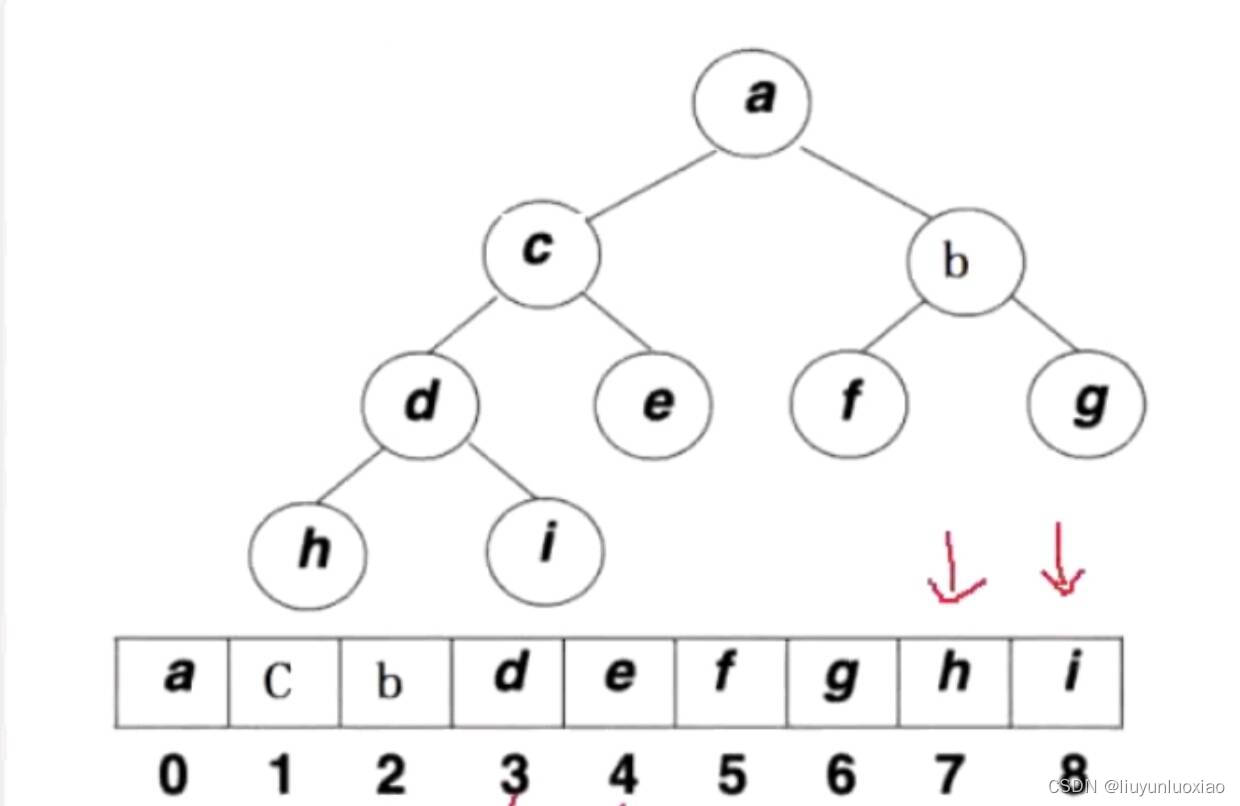
通过下标就可以表现出二叉树的节点之间的关系
左孩子节点（leftchild）下标=父亲节点（parent）下标 *2+1

右孩子节点（rightchild）下标=父亲节点（parent）下标 *2+2

父亲节点（parent）下标=孩子节点（child-1）/2

---

准备工作

创建头文件Heap.h

将头文件和函数定义等放在Stack.h中，方便管理

创建源文件Heap.c

将接口函数的实现放在里面，方便管理

头文件的包含

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

• stdio.h:用于标准输入输出等
• assret.h:用于使用assret函数，实现报错
• stdbool.h：用于使用布尔（bool）类型
• stdlib.h:用于使用动态内存管理函数

---

定义保存堆数据的结构体

为什么要将队列里的数据的数据类型重命名？
这是为了以后如果改变了SL结构体中数据存储的类型时，
不用到处改函数参数等地方的数据类型，只要改typedef后的int 为对应要改成的数据类型就可以。

至于给结构体重命名则仅是为了方便使用

---

初始化

---

销毁堆

---

插入数据

堆的插入是插入在顺序表的末尾，然后在用向上调整算法使插入的数据到达正确位置

---

向上调整算法

向上调整算法：

要求已有的数据是堆

让孩子节点与它的父亲节点比较（假设是大堆）如果孩子节点大于父亲节点，就交换孩子节点和父亲节点，再让原父亲节点成为新的孩子节点
直到孩子节点不再大于父亲节点【因为已有的数据已经是堆】或者孩子节点已经是堆顶（child=0），这样插入的数据就到达了正确的位置，符合大堆的要求：左右孩子节点中存储的数据都必须大于等于父亲节点

图解

可以看见当向上调整算法结束后，新插入的节点已经在正确的位置，并且其他节点也满足大堆的条件

算法代码

交换函数

---

删除堆顶

向下调整算法

向上下调整算法：

要求根的左右子树都是堆

假设是大堆

让左右孩子中更大的那一个与父亲节点的数据比较，如果大于父亲节点的数据就交换孩子节点和父亲节点的数据，再让原孩子节点成为新的父亲节点，循环上述过程直到左右孩子中更大的那一个比父亲节点小或者再产生的左孩子节点越界了（父亲节点已经是最后一层了）

图解

代码

交换函数

---

取出堆顶数据

---

求堆的数据个数

---

判断堆是否为空

堆为空就返回真，不为空就返回假

---

全部代码

Heap.h

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;//初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);

Heap.c

#include"Heap.h"//初始化
void HeapInit(Heap* hp)
{assert(hp);//如果传入的hp为  空  就报错HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType)*4);if (tmp == NULL){printf("HeapInit中mallo失败");exit(-1);//结束程序}hp->a = tmp;hp->capacity = 4;//设置容量为 4hp->size = 0;//size表示数据个数
}// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);//如果传入的hp为  空  就报错free(hp->a);//释放a申请的空间hp->a = NULL;//把a置空，防止野指针hp->capacity = 0;hp->size = 0;
}//交换函数
void Swap(HPDataType* p, HPDataType* q)
{HPDataType tmp = *p;*p = *q;*q = tmp;
}//向上调整算法
void AdjustUP(HPDataType*a,int child)
{int parent = (child - 1) / 2;//通过下标关系找到插入的节点的父亲的下标while (child > 0)//当插入的节点为  堆顶 时结束循环{if (a[child] > a[parent])//如果孩子节点>父亲节点{Swap(&a[child],&a[parent]);//交换对应下标的数据child = parent;//让原来的父亲节点成为  新的  孩子节点parent = (child - 1) / 2;//通过下标关系找到新孩子节点的父亲节点的下标}else//如果孩子节点<=父亲节点{break;//结束循环}}
}// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);//如果传入的hp为  空  就报错if (hp->size == hp->capacity)//如果堆满了就增容{//增容HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * hp->capacity * 2);//在原容量的基础上增加一倍的容量if (tmp == NULL)//tmp为空表示  申请失败{printf("HeapPush中realloc失败");exit(-1);}hp->a = tmp;hp->capacity *= 2;//容量翻倍}hp->a[hp->size] = x;//将数据x插入顺序表末尾hp->size++;//增加数据个数//向上调整算法AdjustUP(hp->a,hp->size-1);//使用向上调整算法让插入的数据到达正确位置
}//向下调整算法
void AdjustDown(HPDataType* a, int parent,int n)
{int child = parent * 2 + 1;//通过下标关系找到左孩子节点的下标while (child < n)//如果孩子节点的下标越界就结束循环{if (child+1<n&&a[child + 1] > a[child])//右孩子下标不能越界，并且右孩子更符合条件{child++;//左孩子下标+1就是右孩子}if (a[child] > a[parent])//如果更符合条件的孩子节点>父亲节点{Swap(&a[child], &a[parent]);//交换对应下标的数据parent = child;//让原来的孩子节点 变成 新的父亲节点child = parent * 2 + 1;//产生新的左孩子下标}else//如果更符合条件的孩子节点<=父亲节点{break;//结束循环}}
}// 堆的删除
void HeapPop(Heap* hp)
{assert(hp);//如果传入的hp为  空  就报错assert(hp->size > 0);//删除数据时堆不能为空Swap(&hp->a[0],&hp->a[hp->size-1]);//交换堆顶和顺序表最后一个数据hp->size--;//size表示有效数据个数，size--就相当于顺序表最后一个数据删除//向下调整算法AdjustDown(hp->a,0,hp->size);//使用向下调整算法让交换到堆顶的数据到达正确位置//让交换后的堆依然满足堆的要求
}// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);//如果传入的hp为  空  就报错assert(hp->size > 0);//取数据时堆不能为空，如果为空就报错return hp->a[0];//堆顶数据就存储在顺序表下标为0的位置
}// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);//如果传入的hp为  空  就报错return hp->size;//size表示有效数据个数
}// 堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);//如果传入的hp为  空  就报错return hp->size == 0;//如果size=0就表示堆为空
}

以上就是全部内容了，如果对你有帮助的话，可以点赞收藏支持一下！