欢迎来到博主的专栏——C语言数据结构
博主ID：代码小豪

树

树是一个非线性的数据结构，由N个结点构成的集合。

树的各个结点由一个根结点联系起来，这个根节点没有前驱元素。

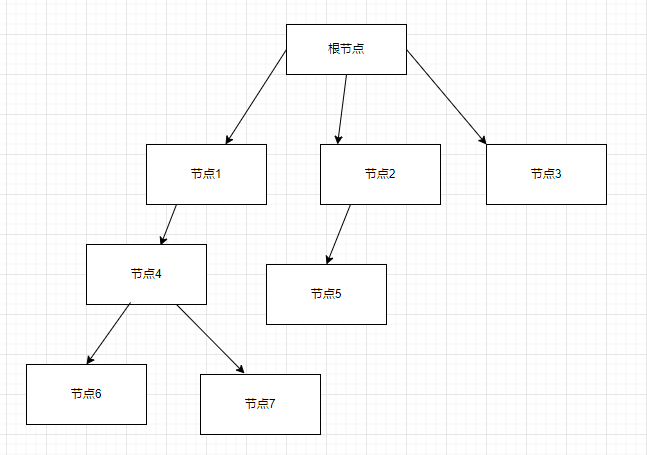
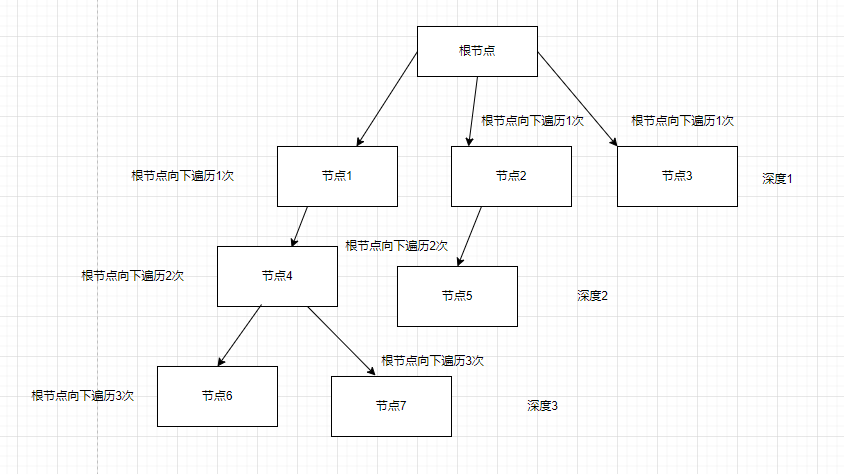
深度

所有能被根节点向下遍历K次访问到的节点同属于同一个深度。
比如：

父子节点
一个节点的下一层结点是子节点，上一层结点被称为父节点。同一层节点被称为兄弟节点。根节点不存在父节点。

度

一个节点拥有的子节点个数，称为该节点的度。

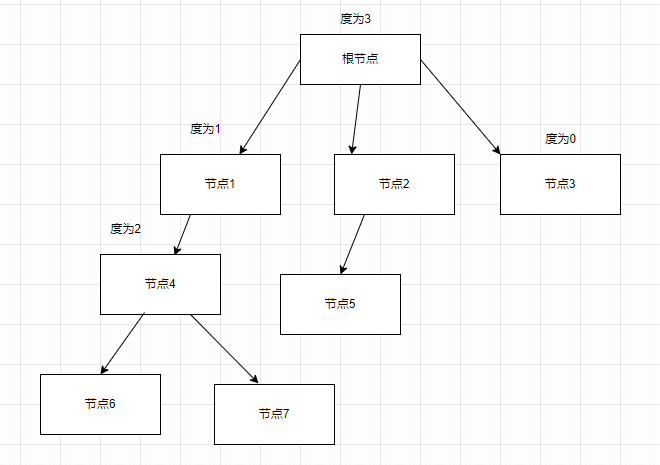
叶子结点，也称终端节点，指的是度为0的节点，比如节点6,7，5,3，这些节点被称为叶节点
树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为3
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推
树的高度或深度：树中节点的最大层次； 如上图：树的高度为4

子树

选取树中除根节点外的任意节点，该节点与其子孙节点构成这个树的子树。

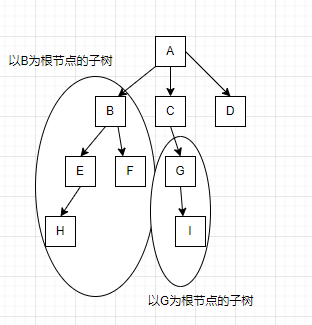
如图中，由B为根节点，B,E,F,H构成一个子树，以G为根结点，G,I构成一个子树。

二叉树

每个节点最多拥有两颗子树，即二叉树的度不超过2.
如下图

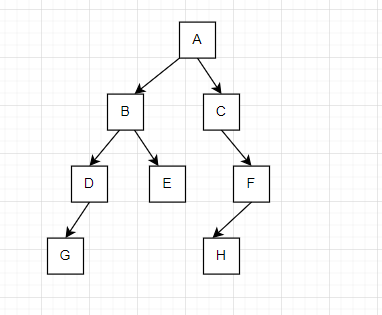
二叉树的特点有：
（1）每个节点最多有两个子树，称为该节点的左子树和右子树。注意所述的是最多两个子树，因此一个子树，或者没有子树都成立。
（2）左子树和右子树是有顺序的，比如F是C的右子树，因为F的是由C的右指针指向的，因此F是右子树。

特殊二叉树

满二叉树

二叉树的所有非叶子节点的度都为2，且最后一层为满的二叉树称为满二叉树

(1)假设满二叉树的深度为N，二叉树的节点数为2^N-1
(2)慢二叉树的第K层的的节点个数为：2^(K-1)

完全二叉树

定义：深度为K的二叉树，将其N个节点按照从上到下，从左到右的顺序进行标号，如果这些节点的标号与满二叉树一一对应，那么这个树称为完全二叉树

如下图

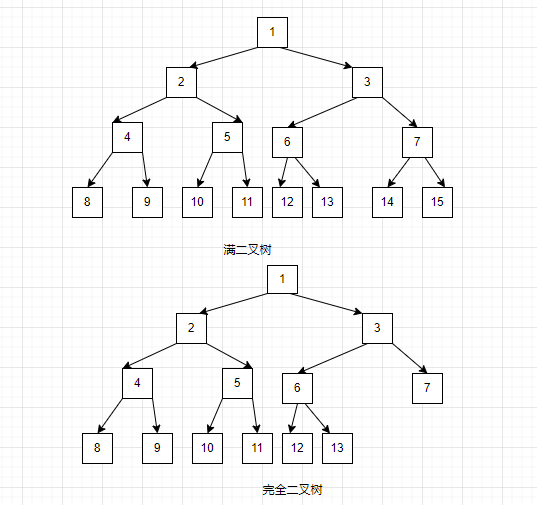
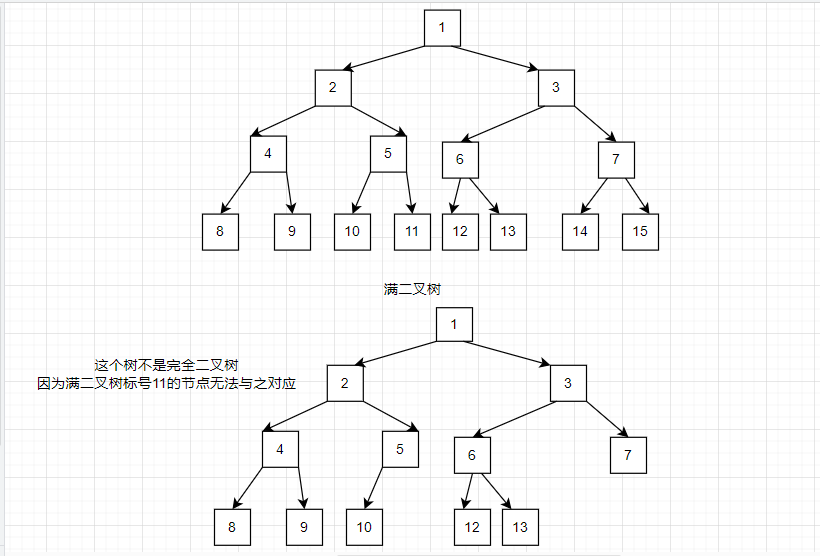
完全二叉树的特点：
（1 ）叶子节点只存在最下两层
（2）最下层的叶子节点一定在左边连续
（3）不存在只有右子树的节点
（4）相同节点数的二叉树，完全二叉树的深度是最小的

完全二叉树的存储结构

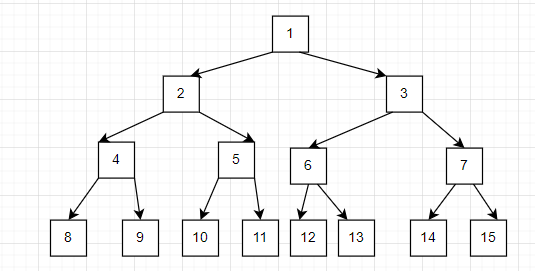
通常情况下，二叉树都会采用链式存储结构，构造一个右指针指向右子树，一个左指针指向左子树。这是因为顺序结构不能展示出二叉树之间的节点关系，以下图二叉树为例。

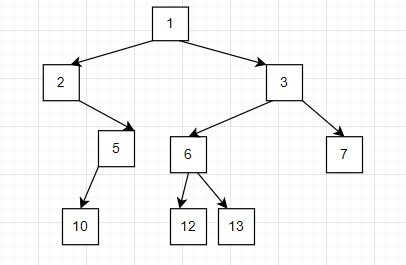
其顺序存储结构为

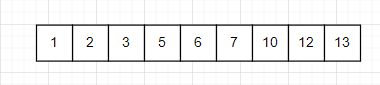
节点12是节点6的子节点，但是顺序结构并不能很好表示这个关系，当然我们可以在结构体中加入父子节点的下标。但是总体而言并不方便

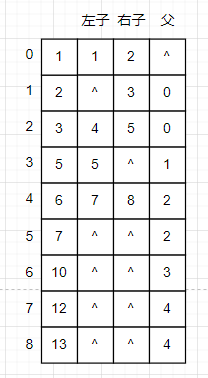
但是满二叉树和完全二叉树适合用顺序结构，这是因为满二叉树和完全二叉树的父子节点具有某种规律

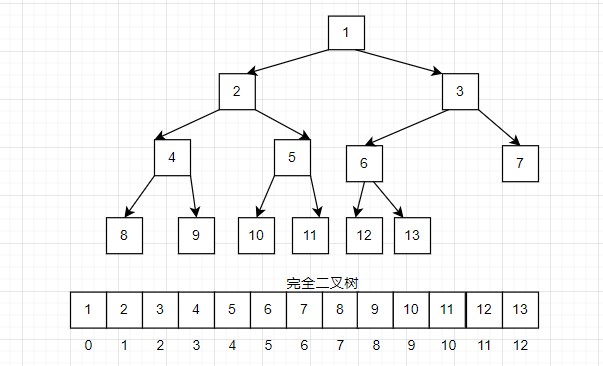
观察上图：完全二叉树的顺序结构拥有两个特点
（1）左子节点的下标等于父节点的下标乘2+1
（2）右子节点的下标等于父节点的下标乘2+2
（3）父节点等于子节点的下标-1除2.

以节点5为例，节点5的下标为4，其左子节点10的下标为9，42+1=9。
右子节点11的下标为10,42+2=10
其父节点2的下标为1,（4-1）/2=1