● 583. 两个字符串的删除操作

注意审题：

给定两个单词 word1 和 word2 ，返回使得 word1 和  word2 相同所需的最小步数。

每步 可以删除任意一个字符串中的一个字符。

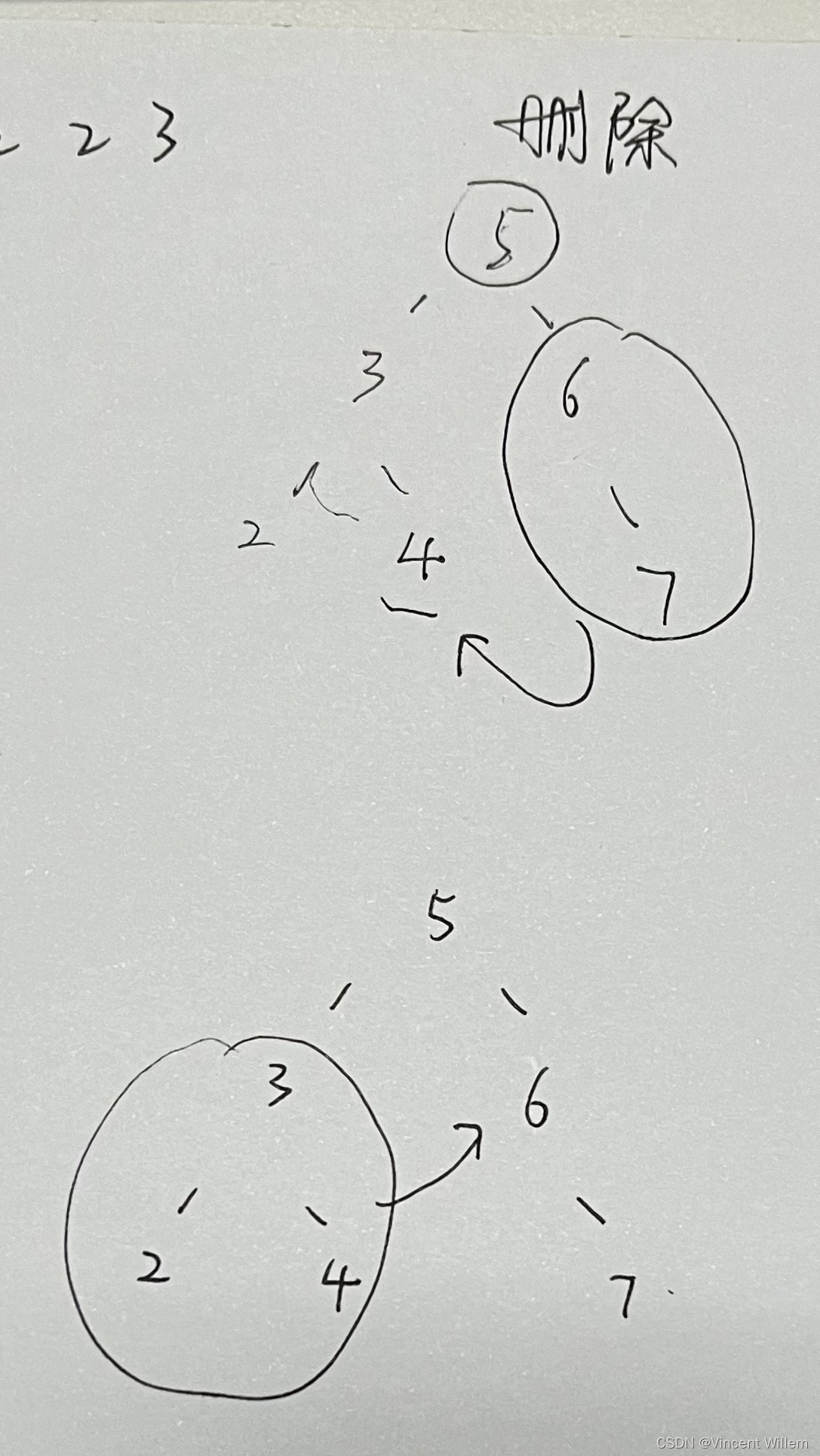
删除最少的字符使两者相同，说明留下来的就是最大公共子序列。不要求连续，所以可以使用● 1143.最长公共子序列 来做，最长公共子序列之外的字母都要删除，所以返回 (n1+n2-2*dp[n1][n2]) 即可。

这是间接求法，直接求：

1.dp数组含义。

dp[i][j]：以word1[i-1]为结尾的字符串，和以word2[j-1]位结尾的字符串，想要达到相等，所需要删除元素的最少次数为dp[i][j]。

2.递推公式。

如果相等：删除次数要最少，那么相等的话就不能删除，得留着，所以dp[i][j]=dp[i-1][j-1];

如果不等：2个字符串没有谁长谁短的前提，所以应该有3种情况。

①可能删掉word1[i-1]，那么dp[i][j]代表的子序列和dp[i-1][j]代表的子序列删除的字母，就多了一个：word1[i-1]，所以dp[i][j]=dp[i-1][j]+1；

②可能删掉word2[j-1]，同样，dp[i][j]=dp[i][j-1]+1；

③都删除。都删除的话，dp[i][j]代表的子序列和dp[i-1][j-1]代表的子序列删除的字母，就多了2个：word1[i-1]和word2[j-1]，所以是dp[i][j]=dp[i-1][j-1]+2；这其实也是满足情况①和情况②的，删掉2个，和dp[i-1][j]相比多删了一个word2[j-1]，和dp[i][j-1]相比多删了一个word1[i-1]。所以情况①/情况②就把③包含了。所以只取①和②的最小删除数量，即Min值就是对的。

dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);

3.初始化。

dp[i][0]。i>0时，word1[i-1]：非空串；word2[0,-1]：空串。所以应该删除word1的前i个达到相等。

dp[0][j]。同样应该删除word2的前j个达到相等。

dp[0][0]。不用删除，=0。

4.遍历顺序。

5.打印。

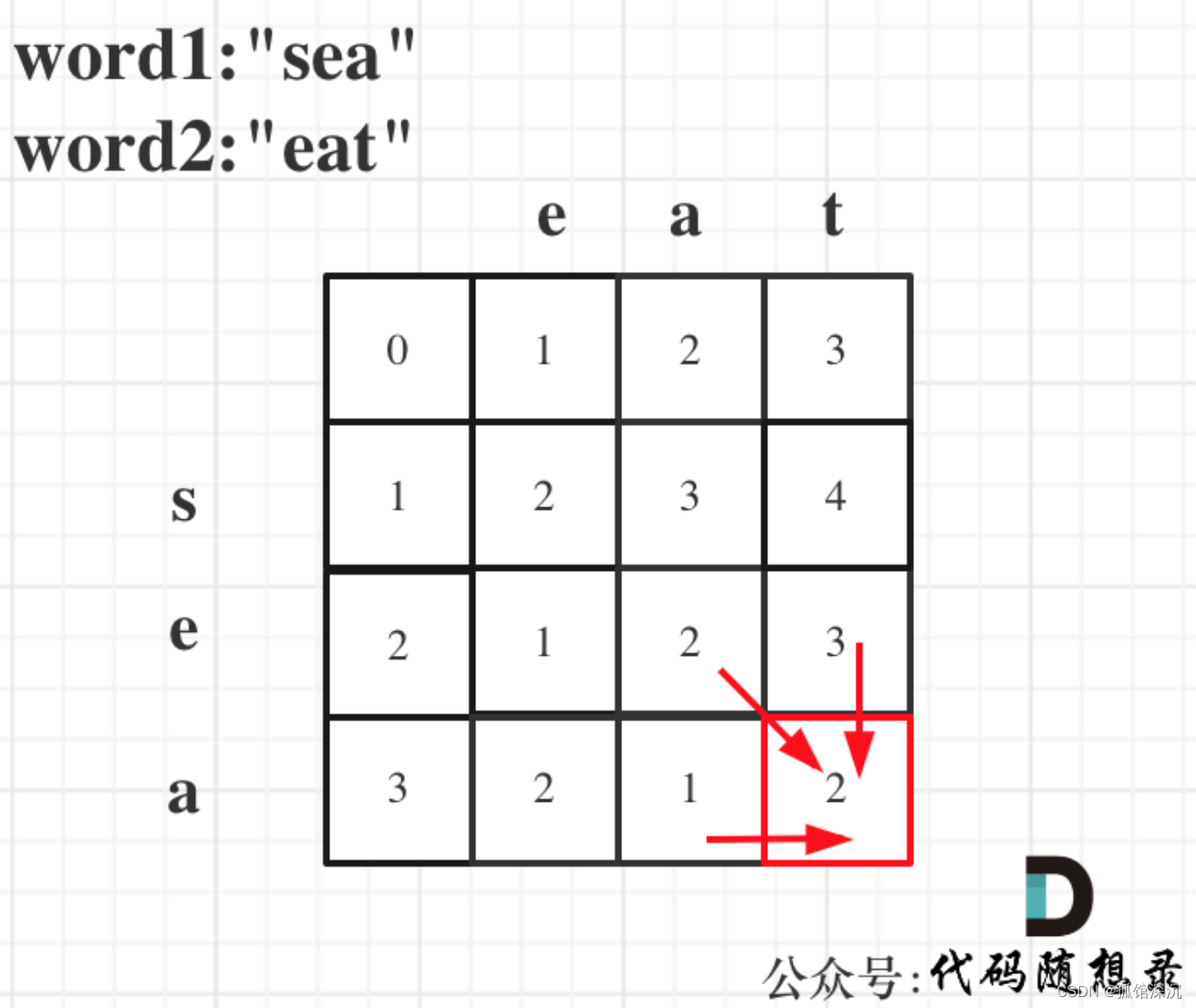
代码如下：

class Solution {
public:int minDistance(string word1, string word2) {int n1=word1.size();int n2=word2.size();vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));for(int i=1;i<=n1;++i)dp[i][0]=i;for(int j=1;j<=n2;++j)dp[0][j]=j;for(int i=1;i<=n1;++i){for(int j=1;j<=n2;++j){if(word1[i-1]==word2[j-1]){dp[i][j]=dp[i-1][j-1];}else{dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);//省略dp[i-1][j-1]+2;}}}return dp[n1][n2];}
};

● 72. 编辑距离

● 编辑距离总结篇