目录
一、基本二叉树
1.1结构
1.2前序遍历(注意三种遍历中Visit所在的位置)
1.2中序遍历
1.3后序遍历
二、真题实战
2.1KY11 二叉树遍历(清华大学复试上机题)【较难】
2.2KY212 二叉树遍历二叉树遍历(华中科技大学复试题)【中等】
一、基本二叉树
1.1结构
首先定义二叉树的结构
struct TreeNode{//数据类型 变量;char data;TreeNode *leftChild; //左子树 TreeNode *rightChild; //右子树 TreeNode(char x) : data(x), leftChild(NULL), rightChild(NULL) {}
};
关于建树,看玩遍历后看题解。
1.2前序遍历(注意三种遍历中Visit所在的位置)
Visit是访问格式,比如print输出,不一定是函数
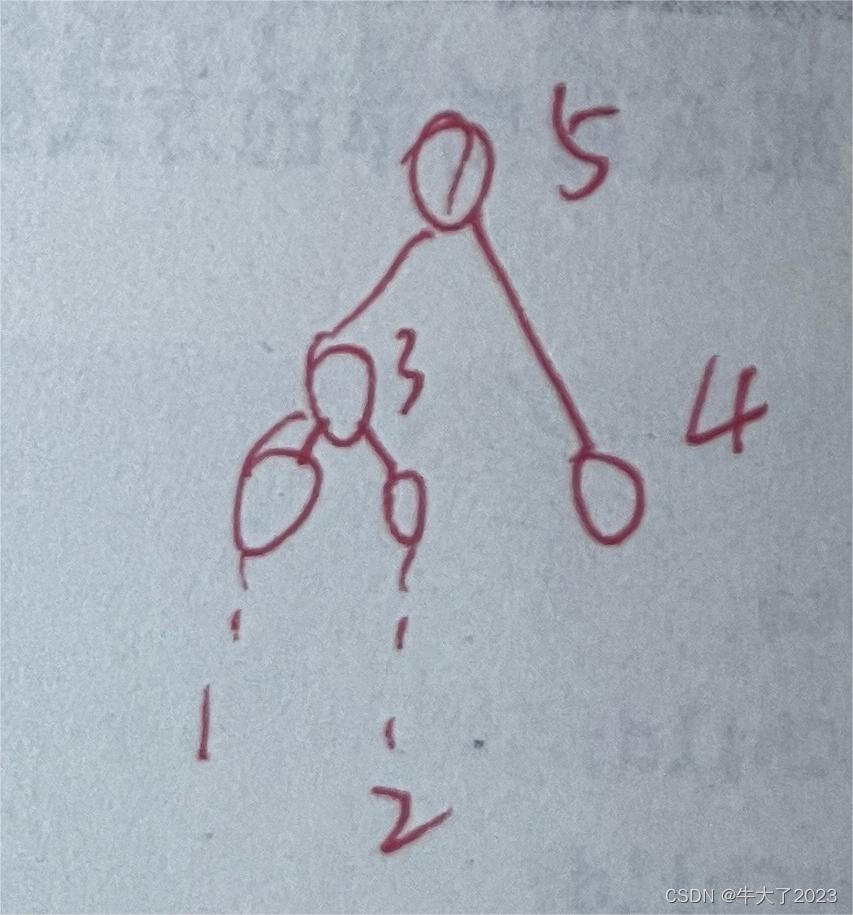
访问根节点-左子树-右子树,遍历过程可以想成逆时针。如图所示。

void PreOrder(TreeNode* root){if(root==NULL){return;}Visit(root->data);PreOrder(root->leftChild);PreOrder(root->rightChild);return ;
}
1.2中序遍历
左-中-右

void InOrder(TreeNode* root){if(root==NULL){return ;}InOrder(root->leftChild);Visit(root->data);InOrder(root->rightChild);return ;
}1.3后序遍历
左-右-根
void PostOrder(TreeNode* root){if(root==NULL){return ;}PostOrder(root->leftChild);PostOrder(root->rightChild);Visit(root->data);return ;
}
1.4层次遍历
暂时没有遇到,先不更,需要用到 队列辅助更新。
二、真题实战
2.1KY11 二叉树遍历(清华大学复试上机题)【较难】
二叉树遍历_牛客题霸_牛客网
描述
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
示例1
输入:
abc##de#g##f###复制输出:
c b e g d f a
总结:注意建立树的顺序和所需变量,root->leftChild或者root->rightChild的赋值。异常情况返回NULL,以及最后返回root。整体就是:确定结构-建树方法-遍历方法-主程序。
#include <bits/stdc++.h>
using namespace std;
struct TreeNode{//数据类型 变量;char data;TreeNode *leftChild; //左子树 TreeNode *rightChild; //右子树 TreeNode(char x) : data(x), leftChild(NULL), rightChild(NULL) {}
};//建树 先序遍历 中-左-右
TreeNode* PreBuild(int& index,string s ){char c=s[index];index++;if(c=='#'){return NULL;}TreeNode* root=new TreeNode(c);root->leftChild=PreBuild(index,s);root->rightChild=PreBuild(index,s);return root;
}void InOrder(TreeNode* root){if(root==NULL){return ;}InOrder(root->leftChild);cout<<root->data<<" ";InOrder(root->rightChild);return ;
}int main() {string s;while(cin>>s){int index=0;TreeNode* root=PreBuild(index,s);InOrder(root);}return 0;
}
2.2KY212 二叉树遍历二叉树遍历(华中科技大学复试题)【中等】
二叉树遍历_牛客题霸_牛客网
描述
二叉树的前序、中序、后序遍历的定义: 前序遍历:对任一子树,先访问根,然后遍历其左子树,最后遍历其右子树; 中序遍历:对任一子树,先遍历其左子树,然后访问根,最后遍历其右子树; 后序遍历:对任一子树,先遍历其左子树,然后遍历其右子树,最后访问根。
给定一棵二叉树的前序遍历和中序遍历,求其后序遍历(提示:给定前序遍历与中序遍历能够唯一确定后序遍历)。
输入描述:
两个字符串,其长度n均小于等于26。 第一行为前序遍历,第二行为中序遍历。 二叉树中的结点名称以大写字母表示:A,B,C....最多26个结点。
输出描述:
输入样例可能有多组,对于每组测试样例, 输出一行,为后序遍历的字符串。
示例1
输入:
ABC BAC FDXEAG XDEFAG复制输出:
BCA XEDGAF
总结:我感觉这个建树比上一个难许多,整道题就是考察建树。
根据先序遍历的性质,第一个节点就是根节点,根据这个入手。(做题时一定要结合数据结构的特性)
再根据中序遍历的性质,找到根节点索引位置的话,左边的就是左子树,右边的就是右子树。再递归处理。
这个根节点索引位置,前序遍历字符串和中序遍历字符串都能用,都是分块节点。
递归停止的标志就是先序遍历字符串长度为0,返回NULL(空节点)。
函数解释:sub = str.substr(7, 5); // 从索引为7的位置提取长度为5的子字符串
sub = str.substr(7);代表从索引7开始到末尾的所有字符串 。


#include<bits/stdc++.h>
using namespace std;
struct TreeNode{char data;TreeNode* leftChild;TreeNode* rightChild;TreeNode(char c):data(c),leftChild(NULL),rightChild(NULL){}
};
TreeNode* Build(string s1,string s2){if(s1.size()==0){return NULL;}char c=s1[0];TreeNode* root=new TreeNode(c);int index=s2.find(c);root->leftChild=Build(s1.substr(1,index),s2.substr(0,index));root->rightChild=Build(s1.substr(index+1),s2.substr(index+1));return root;
}void PostOrder(TreeNode* root){if(root==NULL){return;}PostOrder(root->leftChild);PostOrder(root->rightChild);cout<<root->data;return ;
}int main()
{string s1,s2,s3,s4;cin>>s1>>s2>>s3>>s4;TreeNode* root=Build(s1,s2);PostOrder(root);cout<<endl;TreeNode* root2=Build(s3,s4);PostOrder(root2);return 0;
}![[蓝桥杯练习题]确定字符串是否包含唯一字符/确定字符串是否是另一个的排列](https://img-blog.csdnimg.cn/direct/03007ca25d4e46a28e136723e476fa20.png)




![三. 操作系统 (6分) [理解|计算]](https://img-blog.csdnimg.cn/direct/18d2bbd4478341e0aa06f19bbf5be332.png)