文章目录
- 1. 二维空间
- 1.1 行方向
- 1.2 列方向
- 2. 三维空间
- 2.1 行方向
- 2.2 列方向
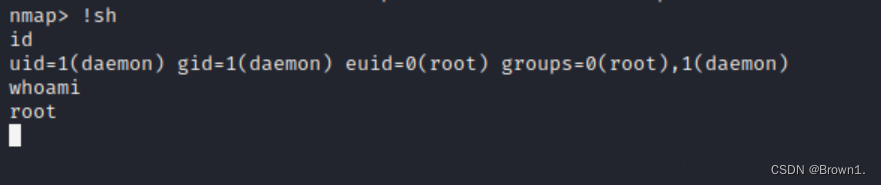
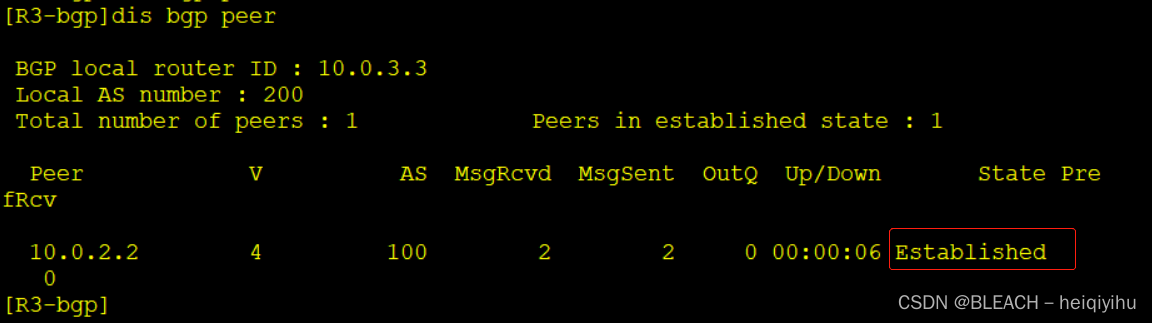
假设有一个方程组 A X = B AX=B AX=B表示如下
2 x − y = 0 (1) 2x-y=0\tag{1} 2x−y=0(1)
− x + 2 y = 3 (2) -x+2y=3\tag{2} −x+2y=3(2)
- 矩阵表示如下:
[ 2 − 1 − 1 2 ] [ x y ] = [ 0 3 ] (3) \begin{bmatrix}2&-1\\\\-1&2\end{bmatrix}\begin{bmatrix}x\\\\y\end{bmatrix}=\begin{bmatrix}0\\\\3\end{bmatrix}\tag{3} 2−1−12 xy = 03 (3)
1. 二维空间
1.1 行方向
- 从行的方向上可以得到如下图形:

- 得到的交点M(1,2) 就是矩阵求得的x=1,y=2答案。
1.2 列方向
将方程变换成列方向,可得如下结构:
x [ 2 − 1 ] + y [ − 1 2 ] = [ 0 3 ] x\begin{bmatrix}2\\\\-1\end{bmatrix}+y\begin{bmatrix}-1\\\\2\end{bmatrix}=\begin{bmatrix}0\\\\3\end{bmatrix} x 2−1 +y −12 = 03
- 可以看成两个向量a= [ 2 − 1 ] \begin{bmatrix}2\\\\-1\end{bmatrix} 2−1 ,b= [ − 1 2 ] \begin{bmatrix}-1\\\\2\end{bmatrix} −12 的线性组合。

- 从列方向可以看出来,方程组可以看出来是以a= [ 2 − 1 ] \begin{bmatrix}2\\\\-1\end{bmatrix} 2−1 ,b= [ − 1 2 ] \begin{bmatrix}-1\\\\2\end{bmatrix} −12 为基,以 x, y 为系数,进行向量计算求得向量 [ 0 3 ] \begin{bmatrix}0\\\\3\end{bmatrix} 03
2. 三维空间
2.1 行方向
2 x − y = 0 ; − x + 2 y − z = − 1 ; − 3 y + 4 z = 4 2x-y=0;\quad-x+2y-z=-1;\quad-3y+4z=4 2x−y=0;−x+2y−z=−1;−3y+4z=4
三维图像如下:

- 我们发现,对于方程组来说,我们从行方向画图的时候发现,特别难找到三个平面的交点,为此我们希望用更简单的方式看方程组(列方向)
2.2 列方向
- 方程组: 2 x − y = 0 ; − x + 2 y − z = − 1 ; − 3 y + 4 z = 4 2x-y=0;\quad-x+2y-z=-1;\quad-3y+4z=4 2x−y=0;−x+2y−z=−1;−3y+4z=4
- 转换成矩阵:
x [ 2 − 1 0 ] + y [ − 1 2 − 3 ] + z [ 0 − 1 4 ] = [ 0 − 1 4 ] x\begin{bmatrix}2\\\\-1\\\\0\end{bmatrix}+y\begin{bmatrix}-1\\\\2\\\\-3\end{bmatrix}+z\begin{bmatrix}0\\\\-1\\\\4\end{bmatrix}=\begin{bmatrix}0\\\\-1\\\\4\end{bmatrix} x 2−10 +y −12−3 +z 0−14 = 0−14 - 从列方向的角度来看,我们是以 a = [ 2 − 1 0 ] , b = [ − 1 2 − 3 ] , c = [ 0 − 1 4 ] a=\begin{bmatrix}2\\\\-1\\\\0\end{bmatrix},b=\begin{bmatrix}-1\\\\2\\\\-3\end{bmatrix},c=\begin{bmatrix}0\\\\-1\\\\4\end{bmatrix} a= 2−10 ,b= −12−3 ,c= 0−14 为基,以x,y,z为系数画图,求得向量 z = [ 0 − 1 4 ] z=\begin{bmatrix}0\\\\-1\\\\4\end{bmatrix} z= 0−14
- 那么我们就可以以更简单的方式进行求解系数x,y,z

- 通过矩阵方程和图形可以看出,当x=0,y=0,z=1时可以得到结果
0 [ 2 − 1 0 ] + 0 [ − 1 2 − 3 ] + 1 [ 0 − 1 4 ] = [ 0 − 1 4 ] 0\begin{bmatrix}2\\\\-1\\\\0\end{bmatrix}+0\begin{bmatrix}-1\\\\2\\\\-3\end{bmatrix}+1\begin{bmatrix}0\\\\-1\\\\4\end{bmatrix}=\begin{bmatrix}0\\\\-1\\\\4\end{bmatrix} 0 2−10 +0 −12−3 +1 0−14 = 0−14 - 只有当向量a,b,c 相互独立,那么就可以通过系数x,y,z来求得向量z;
- AX=b 表示的是将A的列向量进行组合得到向量b.