第18节动态规划一讲-编程知识

1假设有排成一行的N个位置记为1~N，N一定大于或等于2
开始时机器人在其中的M位置上(M一定是1~N中的一个)
如果机器人来到1位置，那么下一步只能往右来到2位置；
如果机器人来到N位置，那么下一步只能往左来到N-1位置；
如果机器人来到中间位置，那么下一步可以往左走或者往右走；
规定机器人必须走K步，最终能来到P位置(P也是1~N中的一个)的方法有多少种
给定四个参数 N、M、K、P，返回方法数

动态规划：如果在调用过程中有重复调用过程就将他存起来

比如递归求斐波那契数列，中间有不少重复过程

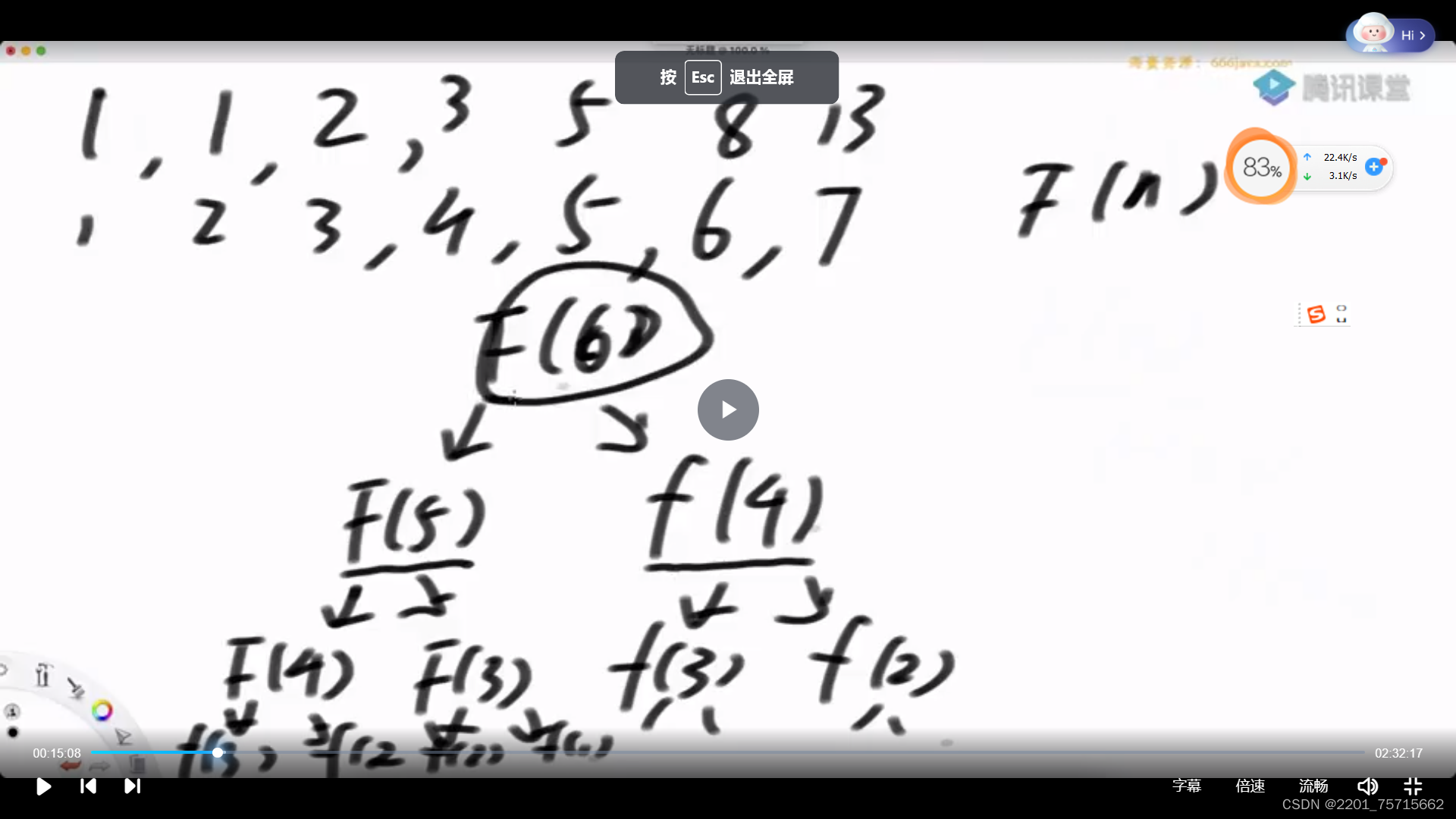
递归策略：

#include <vector>using namespace std;class Solution {
public:int ways1(int N, int start, int aim, int K) {if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {return -1;}return process1(start, K, aim, N);}
/ 机器人当前来到的位置是cur，// 机器人还有rest步需要去走，// 最终的目标是aim，// 有哪些位置？1~N// 返回：机器人从cur出发，走过rest步之后，最终停在aim的方法数，是多少？private:int process1(int cur, int rest, int aim, int N) {if (rest == 0) {return cur == aim ? 1 : 0;}if (cur == 1) {return process1(2, rest - 1, aim, N);}if (cur == N) {return process1(N - 1, rest - 1, aim, N);}return process1(cur - 1, rest - 1, aim, N) + process1(cur + 1, rest - 1, aim, N);}
};

这个递归来进行优化

该递归中出现了重复解

cur范围1到n

rest范围0到k

准备一张dp表，先全设为-1，表示没算过这个过程

#include <vector>using namespace std;class Solution {
public:int ways2(int N, int start, int aim, int K) {if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {return -1;}vector<vector<int>> dp(N + 1, vector<int>(K + 1, -1));return process2(start, K, aim, N, dp);}private:int process2(int cur, int rest, int aim, int N, vector<vector<int>>& dp) {if (dp[cur][rest] != -1) {return dp[cur][rest];}//算过的值就塞入缓存表int ans = 0;if (rest == 0) {ans = cur == aim ? 1 : 0;}else if (cur == 1) {ans = process2(2, rest - 1, aim, N, dp);}else if (cur == N) {ans = process2(N - 1, rest - 1, aim, N, dp);}else {ans = process2(cur - 1, rest - 1, aim, N, dp) + process2(cur + 1, rest - 1, aim, N, dp);}dp[cur][rest] = ans;//没算过的算出来了也塞入缓存表return ans;}
};

再往下优化，直接填这张动态规划表

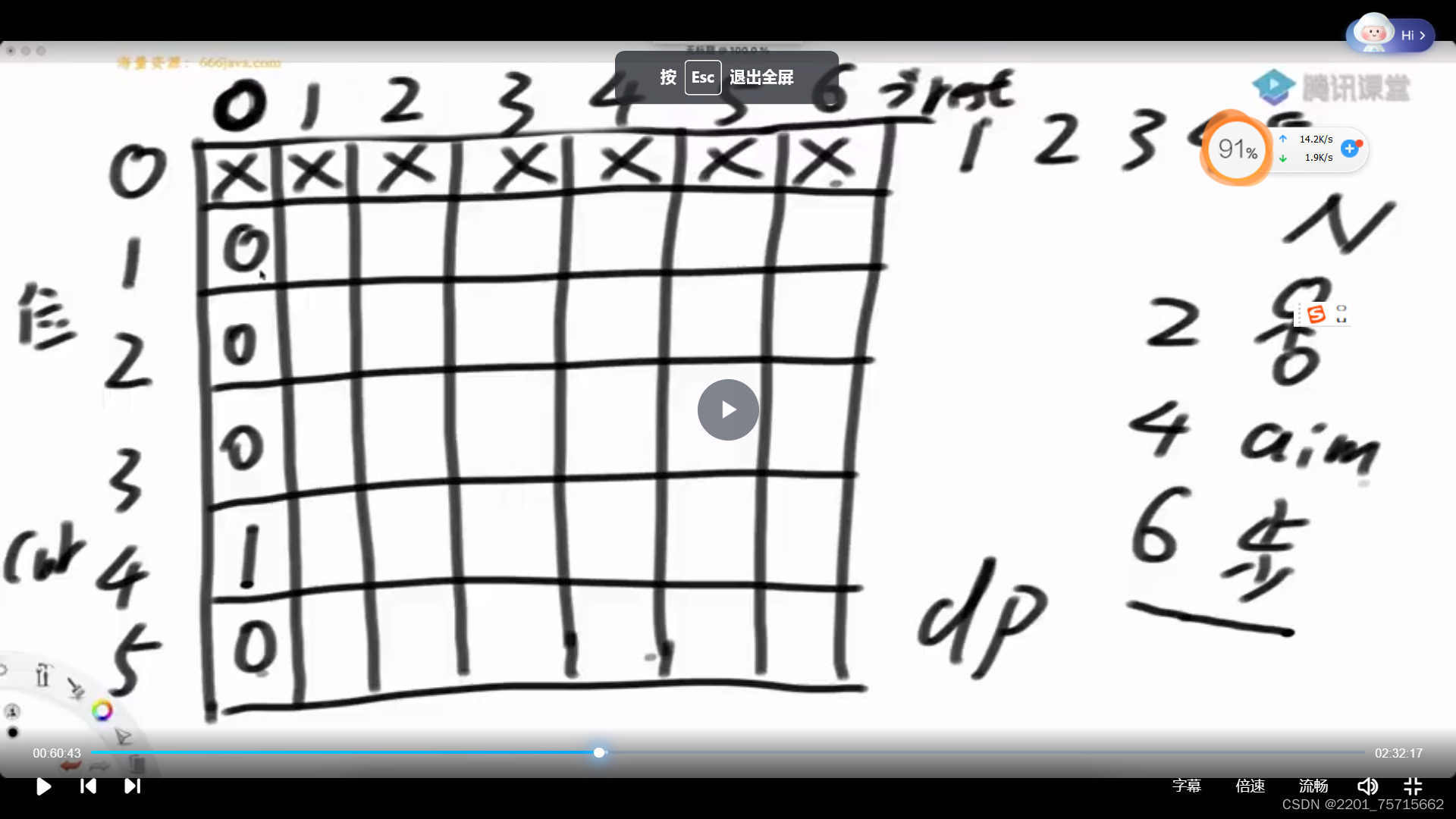
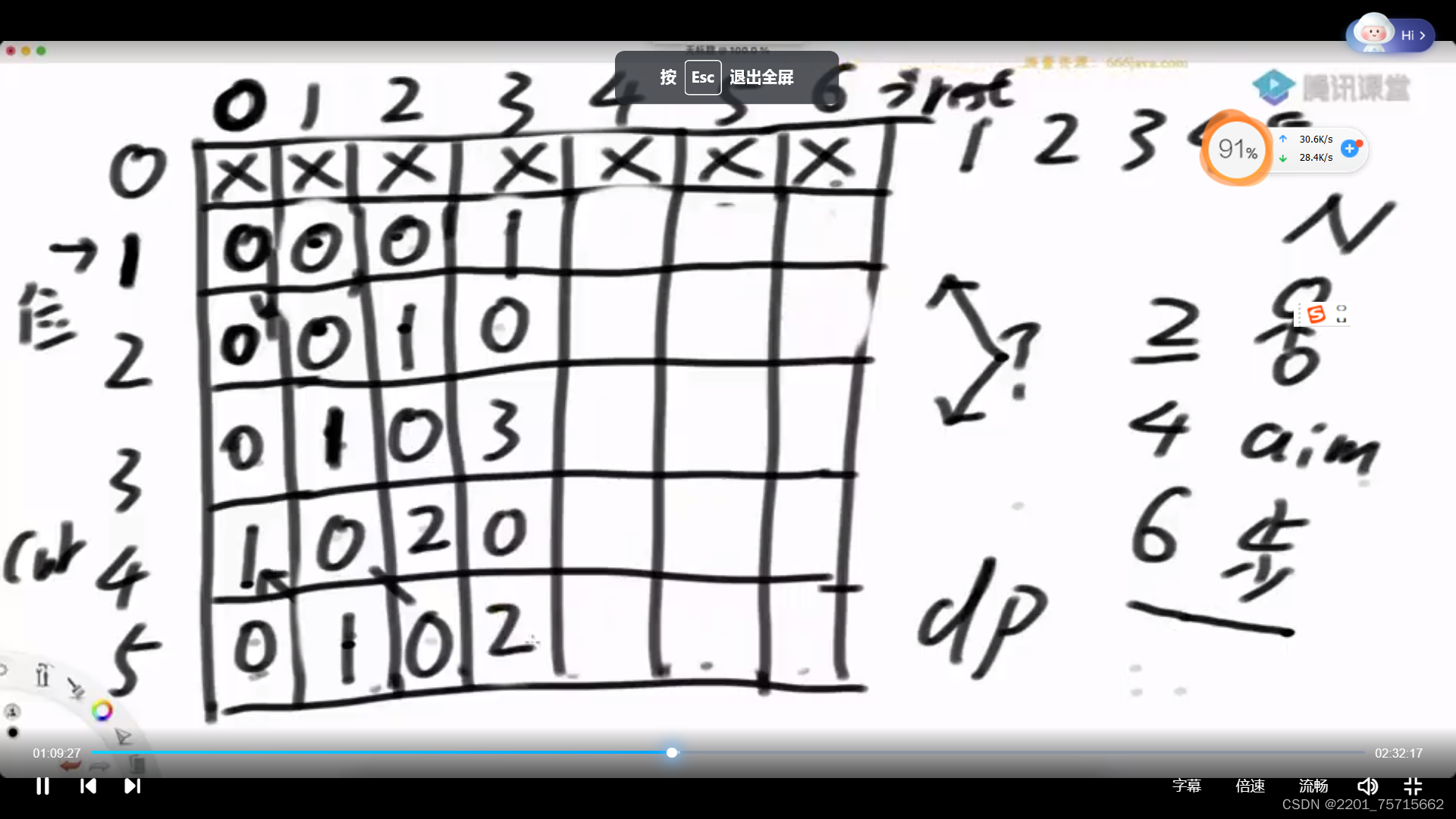
不要硬憋状态转移，要去想尝试策略

#include <vector>using namespace std;class Solution {
public:int ways3(int N, int start, int aim, int K) {if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {return -1;}vector<vector<int>> dp(N + 1, vector<int>(K + 1, 0));dp[aim][0] = 1;for (int rest = 1; rest <= K; rest++) {dp[1][rest] = dp[2][rest - 1];for (int cur = 2; cur < N; cur++) {dp[cur][rest] = dp[cur - 1][rest - 1] + dp[cur + 1][rest - 1];}dp[N][rest] = dp[N - 1][rest - 1];}return dp[start][K];}
};

2给定一个整型数组arr，代表数值不同的纸牌排成一条线
玩家A和玩家B依次拿走每张纸牌
规定玩家A先拿，玩家B后拿
但是每个玩家每次只能拿走最左或最右的纸牌
玩家A和玩家B都绝顶聪明
请返回最后获胜者的分数

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;int f1(vector<int>& arr, int L, int R);
int g1(vector<int>& arr, int L, int R);int win1(vector<int>& arr) {if (arr.empty()) {return 0;}int first = f1(arr, 0, arr.size() - 1);int second = g1(arr, 0, arr.size() - 1);return max(first, second);
}int f1(vector<int>& arr, int L, int R) {if (L == R) {return arr[L];}int p1 = arr[L] + g1(arr, L + 1, R);int p2 = arr[R] + g1(arr, L, R - 1);return max(p1, p2);
}int g1(vector<int>& arr, int L, int R) {if (L == R) {return 0;}int p1 = f1(arr, L + 1, R); // 对手拿走了L位置的数int p2 = f1(arr, L, R - 1); // 对手拿走了R位置的数return min(p1, p2);
}int main() {vector<int> arr = {3, 9, 1, 2};cout << win1(arr) << endl; // 示例输入，输出结果根据实际情况可能不同return 0;
}

弄两张表进行记忆化缓存

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;int f2(vector<int>& arr, int L, int R, vector<vector<int>>& fmap, vector<vector<int>>& gmap);
int g2(vector<int>& arr, int L, int R, vector<vector<int>>& fmap, vector<vector<int>>& gmap);int win2(vector<int>& arr) {if (arr.empty()) {return 0;}int N = arr.size();vector<vector<int>> fmap(N, vector<int>(N, -1));vector<vector<int>> gmap(N, vector<int>(N, -1));int first = f2(arr, 0, arr.size() - 1, fmap, gmap);int second = g2(arr, 0, arr.size() - 1, fmap, gmap);return max(first, second);
}int f2(vector<int>& arr, int L, int R, vector<vector<int>>& fmap, vector<vector<int>>& gmap) {if (fmap[L][R] != -1) {return fmap[L][R];}int ans = 0;if (L == R) {ans = arr[L];} else {int p1 = arr[L] + g2(arr, L + 1, R, fmap, gmap);int p2 = arr[R] + g2(arr, L, R - 1, fmap, gmap);ans = max(p1, p2);}fmap[L][R] = ans;return ans;
}int g2(vector<int>& arr, int L, int R, vector<vector<int>>& fmap, vector<vector<int>>& gmap) {if (gmap[L][R] != -1) {return gmap[L][R];}int ans = 0;if (L != R) {int p1 = f2(arr, L + 1, R, fmap, gmap); // 对手拿走了L位置的数int p2 = f2(arr, L, R - 1, fmap, gmap); // 对手拿走了R位置的数ans = min(p1, p2);}gmap[L][R] = ans;return ans;
}int main() {vector<int> arr = {3, 9, 1, 2};cout << win2(arr) << endl; // 示例输入，输出结果根据实际情况可能不同return 0;
}

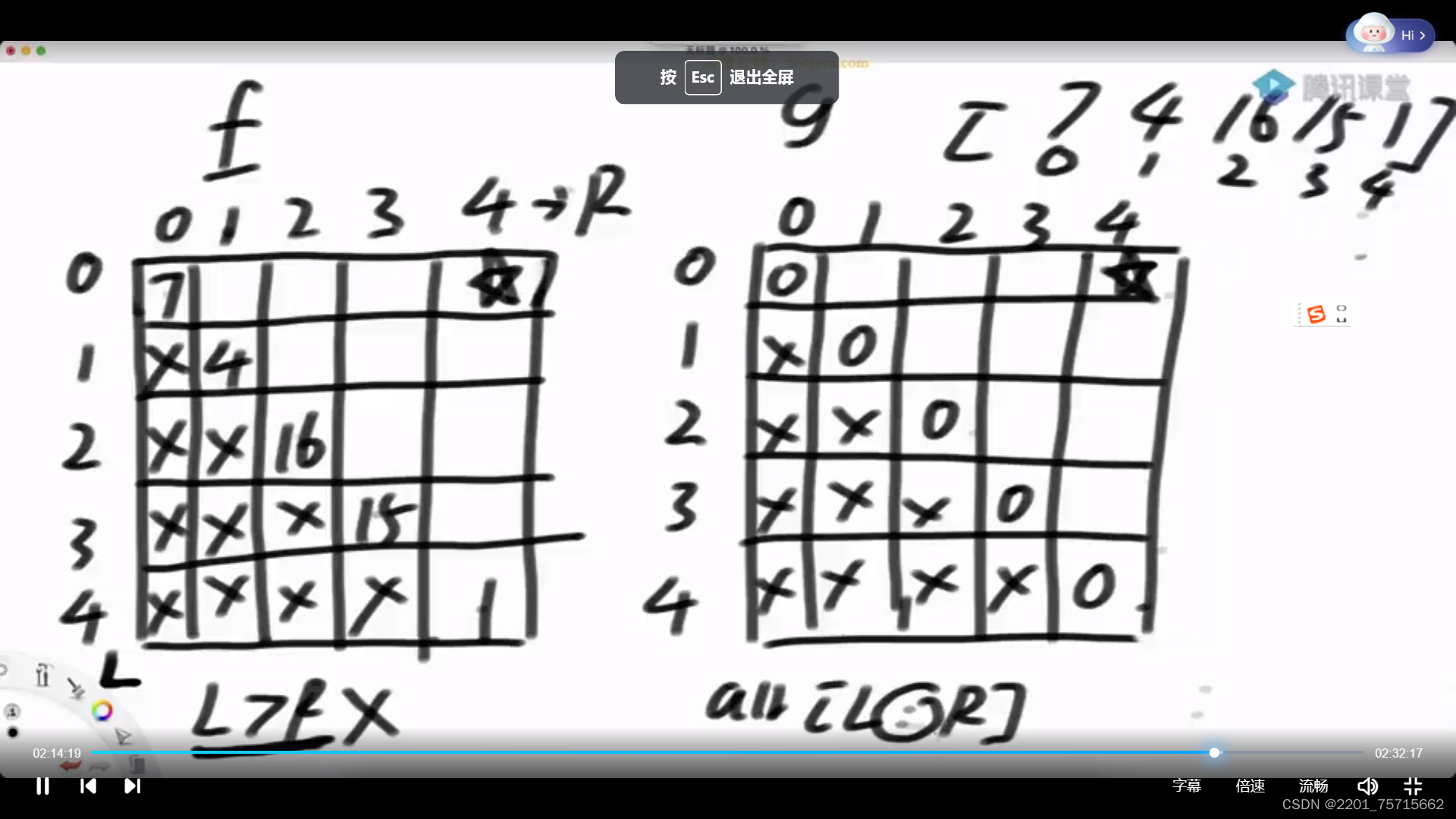
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;int win3(vector<int>& arr) {if (arr.empty()) {return 0;}int N = arr.size();vector<vector<int>> fmap(N, vector<int>(N));vector<vector<int>> gmap(N, vector<int>(N));for (int i = 0; i < N; i++) {fmap[i][i] = arr[i];}for (int startCol = 1; startCol < N; startCol++) {int L = 0;int R = startCol;while (R < N) {fmap[L][R] = max(arr[L] + gmap[L + 1][R], arr[R] + gmap[L][R - 1]);gmap[L][R] = min(fmap[L + 1][R], fmap[L][R - 1]);L++;R++;}}return max(fmap[0][N - 1], gmap[0][N - 1]);
}int main() {vector<int> arr = {3, 9, 1, 2};cout << win3(arr) << endl; // 示例输入，输出结果根据实际情况可能不同return 0;
}