【LetMeFly】2684.矩阵中移动的最大次数:一列一列处理,只记能到哪行(BFS)
力扣题目链接:https://leetcode.cn/problems/maximum-number-of-moves-in-a-grid/
给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ,矩阵由若干 正 整数组成。
你可以从矩阵第一列中的 任一 单元格出发,按以下方式遍历 grid :
- 从单元格
(row, col)可以移动到(row - 1, col + 1)、(row, col + 1)和(row + 1, col + 1)三个单元格中任一满足值 严格 大于当前单元格的单元格。
返回你在矩阵中能够 移动 的 最大 次数。
示例 1:
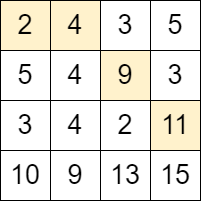
输入:grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]] 输出:3 解释:可以从单元格 (0, 0) 开始并且按下面的路径移动: - (0, 0) -> (0, 1). - (0, 1) -> (1, 2). - (1, 2) -> (2, 3). 可以证明这是能够移动的最大次数。
示例 2:
输入:grid = [[3,2,4],[2,1,9],[1,1,7]] 输出:0 解释:从第一列的任一单元格开始都无法移动。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 1051 <= grid[i][j] <= 106
方法一:一列一列处理,只记能到哪行(BFS + 哈希表set)
不难发现移动的方法有三:↗→↘。不论是哪种移动方式,每移动一步就要往右一列。
因此我们使用一个哈希表记录当前列都能到达哪些位置,由当前列能到达的所有位置获得下一列能到达的所有位置,直到到达最右边一列或无位置可达。
所达到的最远列数即为答案(下标从0开始的话)。
- 时间复杂度 O ( n m ) O(nm) O(nm),其中 g r i d grid grid有 n n n行 m m m列。
- 空间复杂度 O ( n ) O(n) O(n)
AC代码
C++
class Solution {
public:int maxMoves(vector<vector<int>>& grid) {unordered_set<int> can;for (int i = 0; i < grid.size(); i++) {can.insert(i);}int ans = 0;while (can.size()) {ans++;if (ans == grid[0].size()) {break;}unordered_set<int> nextCan;for (int row : can) {for (int j = -1; j <= 1; j++) {if (row + j >= 0 && row + j < grid.size() && grid[row + j][ans] > grid[row][ans - 1]) {nextCan.insert(row + j);}}}swap(can, nextCan);}return --ans;}
};
Python
from typing import Listclass Solution: # AC,80.00%,92.59%def maxMoves(self, grid: List[List[int]]) -> int:can = set(i for i in range(len(grid)))ans = 0while can:ans += 1if ans == len(grid[0]):breaknextCan = set()for row in can:for j in range(-1, 2):if row + j >= 0 and row + j < len(grid) and grid[row + j][ans] > grid[row][ans - 1]:nextCan.add(row + j)can = nextCanreturn ans - 1
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/136757373