一、介绍
欢迎来到“掌握 Python 统计测试:综合指南”,它将介绍本手册中您需要熟悉使用 Python 的所有基本统计测试和分析方法。本文将为您提供统计测试及其应用的全面介绍,无论您是新手还是经验丰富的数据科学家。
使用来自现实世界的实际示例和 Python 代码片段来帮助您理解这些想法,我们将涵盖从假设测试和作为其中一部分进行的测试的所有内容。所以让我们开始吧!
二、Statistics
统计学研究的重点是收集,组织,分析,解释和呈现数据。在将统计应用于科学、工业或社会问题时,通常从统计总体或要研究的统计模型开始。
三、数学中的统计类型
统计数据主要分为两类:
- 描述统计学
- 推论统计
3.1 描述统计学
使用提供的观测结果以这种统计形式汇总数据。汇总是使用平均值或标准差等指标的总体样本的表示形式。
使用表、图形和汇总统计量,描述性统计量是一种排列、描绘和描述数据集合的方法。考虑一个城市使用互联网或电视的人数。
描述性统计也分为四个不同的类别:
- 频率测量
- 色散测量
- 集中趋势的衡量标准
- 位置测量
频率测量显示给定数据发生的频率。离差度量包括范围、方差和标准差。它显示了数据是如何传播的。数据的平均值、中位数和众数是主要趋势。百分位和四分位数等级由位置度量描述。
3.2 推论统计
描述性统计量是使用这种类型的统计量来解释的。换句话说,在收集、检查和总结数据之后,我们使用这些统计数据来解释数据的重要性。或者,换句话说,它用于从易受随机误差(如观测误差、抽样方差等)影响的数据中得出推论。
在推论统计的帮助下,我们可以使用从样本中收集的数据来推断有关人口的结论。它使我们能够提出超出手头事实或数据范围的主张。使用虚构的研究创建估计,作为说明。
四、数据科学中的统计测试
统计检验用于假设检验。 它们可用于确定预测变量和结果变量是否具有统计显著性关系。应估计两组或多组之间的差异。如果数据呈正态分布,则使用参数检验。
统计检验分为两大类:
- 参数
- 非参数
要假设或检查的假设:
一、观察的独立性: 单独的观察值(每个变量条目)彼此无关(例如,对单个患者重复相同的测试会产生非独立的测量值,即重复测量值)。
二、数据正态性:数据服从正态分布。只有定量数据才需要此假设。(有关更多详细信息,另请参阅此处)
三. 方差的同质性:被比较的每个组都有相似的方差(即分数围绕平均值的分布或“散布”)。如果一组的变异明显大于其他组,则检验检测差异的“功效”将降低。
或者,如果您的数据不符合观察独立性的前提,则可以采用考虑这种情况的检验(即重复测量检验)。
相反,如果您的数据不满足正态性或方差齐性假设,则可以执行非参数统计检验,这样您就可以在没有这两个假设的情况下进行比较。
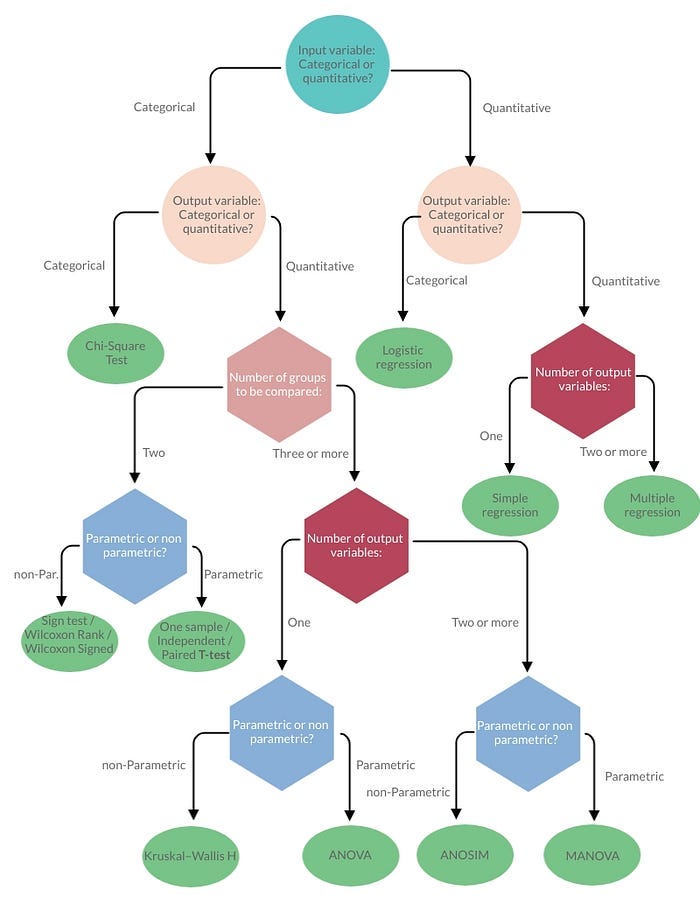
图例.2 — 统计检验选择指南
以下类型的测试用代码解释:
- Z — 测试
- T — 测试
- 方差分析测试
- 卡方检验
- 相关性测试
五、Z 测试
Z 检验是一种统计检验,用于在总体标准差已知时将样本均值与总体均值进行比较。 简单来说,
- 它是一种统计检验,用于确定当方差已知且样本数量较大时,两个总体均值是否不同。
- 它适用于 z 统计量服从正态分布的假设检验。
- Z 统计量或 Z 分数是表示 Z 检验结果的数字。
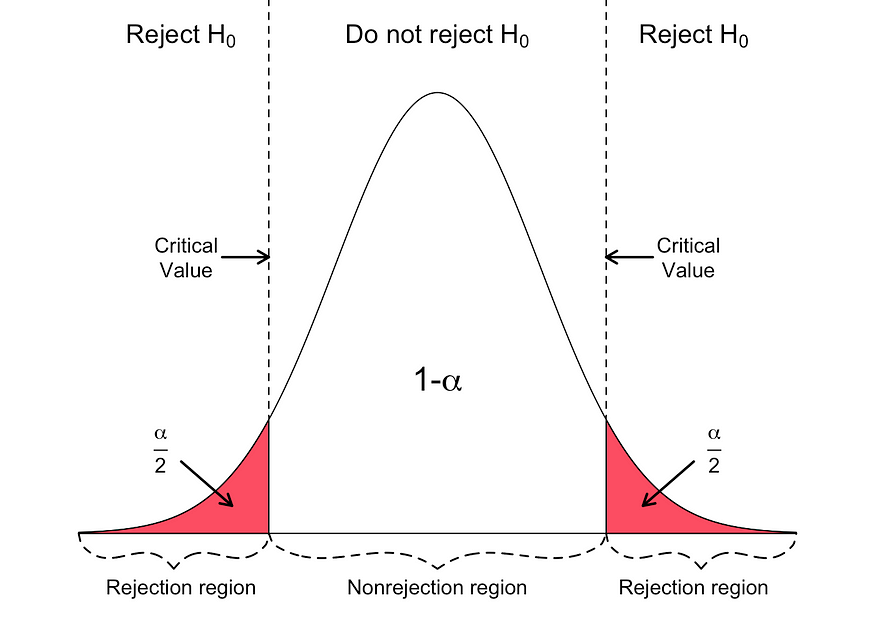
为了理解 Z 检验,让我们看一个真实世界的例子。假设一家鞋业公司声称他们的鞋类的典型寿命是 500 天。我们收集了50双鞋的样本来验证这一断言,我们发现平均寿命为490天,标准差为25天。我们现在可以运行 Z 测试以查看样本是否支持公司的说法。
何时使用 Z 检验:
- 样本数量应大于 30。否则,我们应该使用 t 检验。
- 样本应从总体中随机抽取。
- 应该知道总体的标准差。
- 从总体中抽取的样本应彼此独立。
- 数据应呈正态分布,但对于大样本量,假定数据具有正态分布。
执行 Z 检验的步骤:
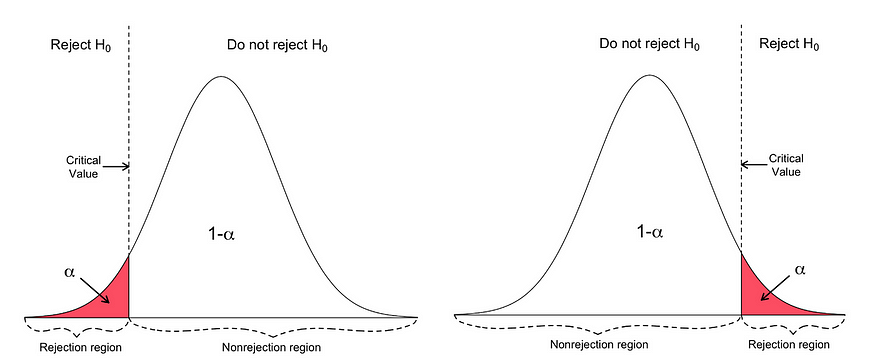
- 首先,确定零假设和替代假设。
- 确定显著性水平 (∝)。
- 使用 在 z 检验中查找 z 的临界值。
- 计算 z 检验统计量。下面是用于计算 z 检验统计量的公式。
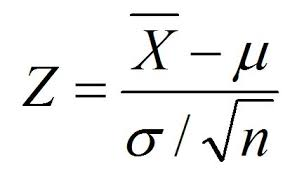
如果 p 值低于阈值(表示小于),则可以推断输入变量和目标变量之间存在统计显著性关系。
否则,您可以推断预测变量和结果变量之间没有统计显著性关系。
5.1 Python 中的一个示例 Z 测试
假设某个人群中的智商呈正态分布,平均值为 μ = 100,标准差为 σ = 15。
一位研究人员想知道一种新药是否会影响智商水平(是或否[分类]),因此他招募了20名患者进行尝试并记录他们的智商水平。
以下代码演示如何在 Python 中执行单样本 z 检验,以确定新药是否会导致智商水平的显着差异:
from statsmodels.stats.weightstats import ztest as ztest
"""
H0 : New Drug not Affects the IQ
H1 : New Drug Does Affects the IQ
"""#enter IQ levels for 20 patients
data = [88, 92, 94, 94, 96, 97, 97, 97, 99, 99,105, 109, 109, 109, 110, 112, 112, 113, 114, 115]#perform one sample z-test
ztest(data, value=100)一个样本 z 检验的检验统计量为 1.5976,对应的 p 值为 0.1101。
由于此 p 值不小于 .05,因此我们没有足够的证据来否定原假设。换句话说,新药不会显着影响智商水平。
5.2 Python 中的两个示例 Z 测试
假设已知两个不同城市中个人的智商水平以已知的标准差呈正态分布。
研究人员从每个城市选择20人的基本随机样本,并记录他们的智商水平,以确定城市A和B中人们的平均智商水平是否彼此不同。

以下代码演示如何在 Python 中执行双样本 z 检验,以确定两个城市之间的平均 IQ 水平是否不同:
from statsmodels.stats.weightstats import ztest as ztest"""
H0 : Mean is not Different
H1 : Mean is Different
"""#enter IQ levels for 20 individuals from each city
cityA = [82, 84, 85, 89, 91, 91, 92, 94, 99, 99,105, 109, 109, 109, 110, 112, 112, 113, 114, 114]cityB = [90, 91, 91, 91, 95, 95, 99, 99, 108, 109,109, 114, 115, 116, 117, 117, 128, 129, 130, 133]#perform two sample z-test
ztest(cityA, cityB, value=0) 两个样本 z 检验的检验统计量为 -1.9953,对应的 p 值为 0.0460。
由于此 p 值小于 .05,因此我们有足够的证据来否定原假设。换句话说,两个城市的平均智商水平存在显着差异。
六、T 检验
T 检验统计检验用于确定两组均值之间是否存在显著差异。相对于两组均值之间的变异,它估计分组内的方差。当样本量较小且总体标准差未知时,此检验特别有用。
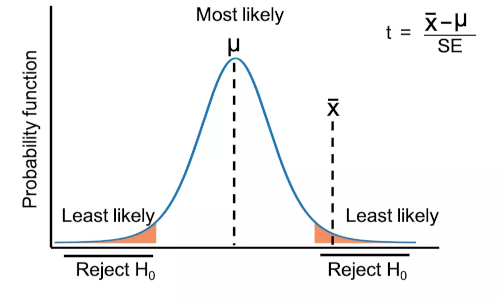
- T 检验是一种参数化推论统计方法,用于比较两个不同组之间的均值(双样本 t 检验)或与特定值(单样本 t 检验)。
- 在 t 检验中,检验统计量遵循原假设下的 t 分布(连续概率分布的类型)。
- t 检验是专门为小样本量数据 (n 30) 创建的,而 z 检验需要更高的样本量(t 和 z 分布与较大的样本量相似,例如 n=30)。t 检验也适用于样本量非常小 (n 5) 的数据。对于样本数量有限的数据集,t 检验会产生更保守的结果。
- T 检验有三种主要类型:一个样本 t 检验、双样本 t 检验(非配对或独立)和配对 t 检验。
- 单样本 t 检验将样本均值与假设值进行比较,而双样本 t 检验(也称为独立或未配对 t 检验)比较两个独立组的均值。在配对 t 检验中比较两个因变量之间的差异。
一个样本 t 检验
- 一个样本 t 检验(单样本 t 检验)用于将样本均值(总体中的随机样本)与特定值(总体的假设或已知均值)进行比较。
- 例如,一个球的直径为 5 厘米,我们要检查从生产线上随机抽取的样本(例如 50 个球)中球的平均直径是否与已知尺寸不同。
假设
- 因变量应具有近似正态分布(夏皮罗-威尔克斯检验)
- 观测值彼此独立
假设
- 原假设:样本均值等于假设或已知总体均值
- 备择假设:样本均值不等于假设或已知总体均值(双尾或双侧)
- 备择假设:样本均值大于或小于假设或已知总体均值(单尾或单侧)。

from scipy import stats as st
from bioinfokit.analys import get_data
# load dataset as pandas dataframe
df = get_data('t_one_samp').data
df.head(2)
# output
#size
#0 5.739987
#1 5.254042# t test using scipy
a = df['size'].to_numpy()
# use parameter "alternative" for two-sided or one-sided test
st.ttest_1samp(a=a, popmean=5)# Using only Bioinfokit
from bioinfokit.analys import stat
res = stat()
res.ttest(df=df,test_type=1, res='size',mu=5)
print(res.summary)从一个样本 t 检验获得的 p 值不显著 (p > 0.05),因此,我们得出结论,随机样本中球的平均直径等于 5 cm。
6.1 两个样本 t 检验
双样本(未配对或独立)t 检验通过比较两个独立组的均值是否相等或统计上不同来评估它们。在双样本 t 检验中,通常计算来自两组的样本均值,并为从中选择两组的总体均值(未知均值)形成结论。
例如,我们有两种不同的植物基因型(基因型A和基因型B),我们想看看基因型A的产量是否与基因型B有很大不同。
假设
- 原假设:两个组均值相等
- 备择假设:两个组均值不同(双尾或双侧)
- 备择假设:一个组的平均值大于或小于另一个组(单尾或单侧)
假设
- 两组中的观测值具有近似正态分布(夏皮罗-威尔克斯检验)
- 方差的同质性(治疗组之间的方差相等)(莱文或巴特利特检验)
- 两组从同一人群中彼此独立地抽样。
注意:当样本数量较大 (n ≥ 30) 且两组中样本数相等 (n1 = n2) 时,两个样本 t 检验对方差的正态性和同质性假设相对稳健。
如果样本数量较小且不服从正态分布,则应使用非参数曼-惠特尼 U 检验。
两个样本(独立)t检验公式 -

如果方差相等,则双样本 t 检验和韦尔奇检验(不等方差 t 检验)的性能相同(就类型 I 错误率而言)并且具有相似的功效。
计算 Python 中的两个样本 t 检验:
# Perform two sample t-test using SciPy
# install bioinfokit as !pip install bioinfokit
!pip install bioinfokit
from scipy import stats as st
from bioinfokit.analys import get_data
# load dataset as pandas dataframe
df = get_data('t_ind_samp').data
df.head(2)a = df.loc[df['Genotype'] == 'A', 'yield'].to_numpy()
b = df.loc[df['Genotype'] == 'B', 'yield'].to_numpy()
st.ttest_ind(a=a, b=b, equal_var=True)# Perform two sample t-test using bioinfokit
from bioinfokit.analys import stat
res = stat()
# for unequal variance t-test (Welch's t-test) set evar=False
res.ttest(df=df, xfac="Genotype", res="yield", test_type=2, evar=False)
print(res.summary)注意:尽管当两组的样本数量不相同时可以进行 t 检验,但每组中具有相等的样本数量以提高 t 功效会更有效。测试的
从t检验获得的p值是显著的(p <0.05),因此,我们得出结论,基因型A的产量与基因型B显着不同。
6.2 配对 t 检验
- 配对t检验用于比较同一受试者的一对因变量之间的差异
- 例如,我们有植物品种A,想比较施用一些肥料前后A的产量。
- 注意:配对 t 检验是对两个因变量之间差异的单样本 t 检验
假设
- 原假设:两个因变量之间没有差异(差值 = 0)
- 备择假设:两个因变量(双尾或双侧)之间存在差异
- 备择假设:大于或小于零的两个响应变量之间的差异(单尾或单侧)
假设
- 两个因变量之间的差异遵循近似正态分布(夏皮罗-威尔克斯检验)
- 自变量应具有一对因变量
- 两个因变量之间的差异不应具有异常值
- 观测值彼此独立地采样

图例.10 — 统计中的配对 t 检验
# install bioinfokit as !pip install bioinfokit
from bioinfokit.analys import get_data, stat
# load dataset as pandas dataframe
# the dataset should not have missing (NaN) values. If it has, it will omitted
df = get_data('t_pair').data
df.head(2)res = stat()
res.ttest(df=df, res=['AF', 'BF'], test_type=3)
print(res.summary)t检验得到的p值显著(p<0.05),因此,我们得出结论,施肥显著提高了植物品种A的产量。
注意:如果您有部分配对的数据,则可以对所有未配对的观测值执行配对 t 检验,或者通过将两个因变量视为两个单独的样本来使用独立 t 检验。然而,这两种临时办法都不合适,因为它们不能满足基本条件,并可能导致对方差的偏斜估计和信息丢失。
- 如果效应量较大且数据遵循 t 检验假设,则 t 检验可以应用于极小样本数量(n = 2 至 5)。请记住,较大的样本量优于较小的样本量。
- 对于配对 t 检验,建议具有较高的对内相关性 (r > 0.8),以获得小样本量数据的高统计功效 (>80%)。
- 当样本数量较大 (n ≥ 30) 时,t 检验对方差的正态性和同质性假设相对稳健。
在下一篇博客中,我将讨论卡方检验、方差分析和相关性检验
七、结语
通过使用 Python 深入学习 T 检验和 Z 检验,您可以掌握数据分析并开发可靠的结果。Z 检验用于评估有关总体均值的假设,而 T 检验用于发现两组之间是否存在显著差异。凭借对这些统计测试的经验和工作掌握,您将能够处理具有挑战性的问题并为您的公司提供有见地的建议。




![[OGeek2019 Final]OVM——详细入门VM pwn](https://img-blog.csdnimg.cn/280860e8ac984172b35270870f153ff4.png)