Python程序设计基本数据类型及操作-编程知识

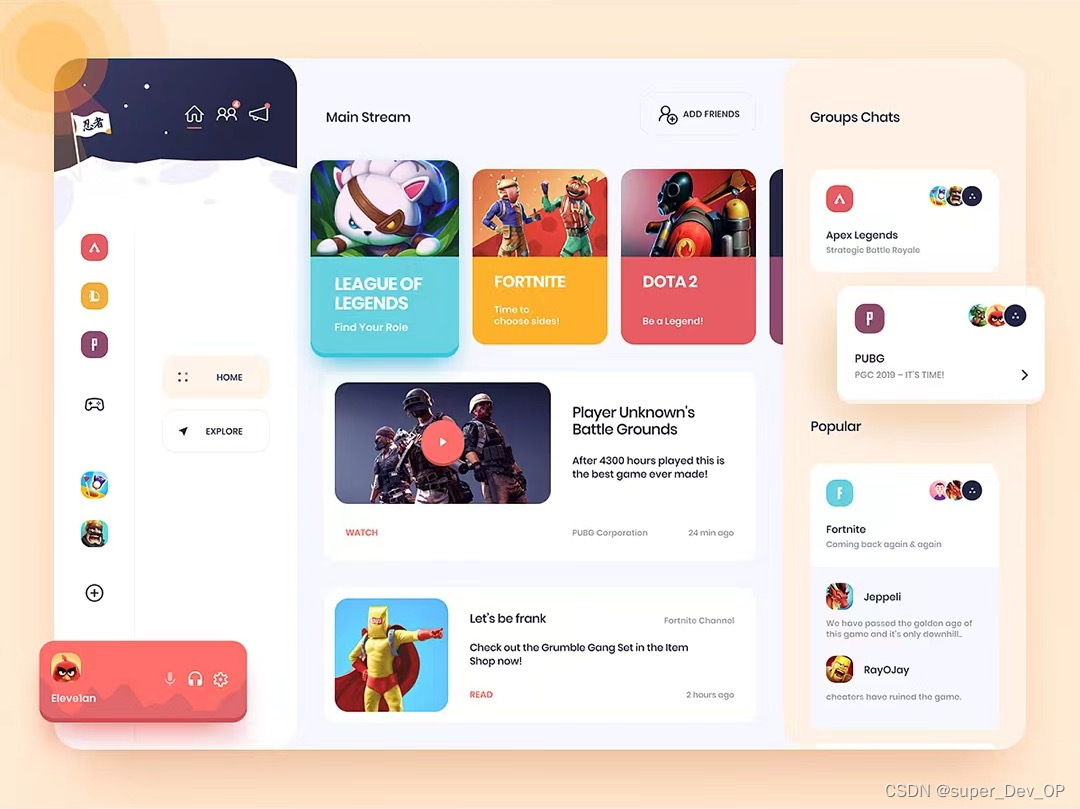
1.计算一元二次方程的根

编写一个计算一元二次方程的根的小程序。一元二次方程经过整理都可化成一般形式ax²+bx+c=0（a≠0）。其中ax²叫作二次项，a是二次项系数；bx叫作一次项，b是一次项系数；c叫作常数项。由一元二次方程求根公式知

a=eval(input("输入二次项系数"))
b=eval(input("输入一次项系数"))
c=eval(input("输入常数项"))x1 = (-b + (b**2-4*a*c)**0.5) / (2*a)
x2 = (-b - (b**2-4*a*c)**0.5) / (2*a)print("方程的根是{:.2f}和{:.2f}".format(x1,x2))

2.计算三角形的面积

编写一个计算三角形面积的小程序。已知三角形两边a,b,两边夹角为c（角度），则三角形面积s=(a×b×sin⁡(c))/2 ，即两夹边之积乘夹角的正弦值。

a=eval(input("输入边长一"))
b=eval(input("输入边长二"))
c=eval(input("输入夹角"))import math
d = math.sin(c*math.pi/180)
s = (a * b * d)/2
print("三角形面积{:.2f}".format(s))

3.计算投资收益

编写一个能计算投资收益的程序。某客户有500000元投资十年。一种投资方式是购买一年期的大额存单，年利率为3.15%。每到年底，客户将本金和利息继续转存。另一种方式是购买公寓，每月获得租金1500元。每到年底，客户将利息存为一年定期。活期存款的年利率为1.75%。计算十年来这两种投资方式下用户每年的累计收益

x = 500000
y = 0
for i in range(1,11):x = x + x * 0.0315y = 18000 + y + y * 0.0175print("第%d年方案一%.2f方案二%.2f" % (i, x-500000, y))

4.计算普通年金终值

编写一个计算普通年金终值的小程序。普通年金终值是指最后一次支付时的本利和，它是每次支付的复利终值之和。按复利换算到最后一期期末的终值，然后加总，就是该年金终值。

A=eval(input("请输入每年本金"))
i=eval(input("请输入利率"))
n=eval(input("请输入年限"))F = A * (((1 + i) ** n - 1)/i)print("普通年金终值是{:.2f}".format(F))

5.计算三角形的周长和面积

编写一个计算三角形的周长和面积的小程序。海伦公式是利用三角形的三条边的边长直接求三角形面积的公式。假设在平面内，有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得：

a=eval(input(""))
b=eval(input(""))
c=eval(input(""))p = (a + b + c) / 2
s = (p * (p - a)*(p - b)*(p - c))**0.5
print("三角形周长{:.2f}三角形面积{:.2f}".format(2*p, s))

6.计算四边形的周长和面积

编写一个能计算四边形的周长和面积的小程序。输入四边形的四条边长和一对对角之和（角度值），计算其周长和面积。四边形四个边的长度为 a,b,c,d,一对对角之和为 m，x是周长的一半，其面积为

from math import *
a=eval(input("请输入边长一"))
b=eval(input("请输入边长二"))
c=eval(input("请输入边长三"))
d=eval(input("请输入边长四"))
m=eval(input("请输入对角之和"))import math
z = a + b + c + d
x = z / 2
s = ((x-a)*(x-b)*(x-c)*(x-d) - a*b*c*d*math.cos(math.radians(m / 2))**2)**0.5print("四边形周长{:.2f}面积{:.2f}".format(z,s))

7.水仙花数

编写一个程序，显示所有的水仙花数水仙花数是一个三位数，其百位、十位、个位的数字的立方之和为其数本身。例如 153的各数立方之和为1+125+27=153

for i in range(100,1000):x1 = i % 10 # 个位x2 = i // 10 % 10 # 十位x3 = i // 100 # 百位sum1 = x1*x1*x1 + x2*x2*x2 + x3*x3*x3if (i == sum1):print(i)

8.计算投资收益

编写一个能计算投资收益的程序。某客户有本金 500000 元，有两个投资方案。一是某银行大额存单，三年期的存款年利息是每年4%，该客户存款到期后将利息和本金再存入。二是购买公寓出租，每月租金 1000 元，该客户每年年底将租金采取一年期定期存款的形式，年利率为 1.75% 计算30年中每三年该客户两种投资方案的投资收益。

x = 500000
y = 0
for i in range(1,31):y = 1000*12 + y + y * 0.0175if i % 3 == 0:x = x + x * 0.04 * 3print("第{:2}年公寓方案{:.2f}大额存单投资收益{:.2f}".format(i,y,x-500000))

9.采用年度总和法计算固定资产折旧

编写一个使用年度总和法计算固定资产折旧的小程序。某企业有一项固定资产。该项固定资产原始价值x元，预计使用年限为n年，预计净残值为y元输入x,n,y,要求计算采用年数总和法计提各年的折旧额。

年数总和法，又称合计年限法，是将固定资产的原价减去预计净残值后的余额，乘以一个以固定资产尚可使用寿命为分子，以预计使用寿命逐年数字之和为分母的逐年递减的分数计算每年的折旧额。计算公式如下：年折旧率=尚可使用寿命／预计使用寿命的年数总和年折旧额=（固定资产原价-预计净残值）×年折旧率

x=eval(input("固定资产原始价值"))
y=eval(input("预计净残值"))
n=eval(input("使用年限"))
#代码开始
x1 = 0
sum1 = 0
for j in range(1,n+1):sum1 = sum1 + jfor i in range(n, 0, -1):s = (x - y) * i / sum1 x1 = x1 + sprint("第{}年折旧额{:.2f}剩余价值{:.2f}".format(n+1-i,s,x-x1))

10.无收益资产远期合约价值

无收益资产是指在远期到期前，不产生现金流的资产，如贴现债券。无收益资产远期合约价值等于资产现货价格与交割价格现值的差额，如下图所示。

S为资产现货价格，K为远期合约的交割价格，r为无风险年利率，T为远期合约的到货时间，t是现在的时间，T-t代表远期合约距离到期时间的剩余时间，均以年为单位，例如，6个月期的无风险年利率为4.17%。市场上正在交易一份标的证券为一年期贴现债券、剩余期限为6个月的远期合约多头，其交割价格为970元，该债券的现价为960元。其远期价值为 S=960，K=970，r=4.17%，T-t=0.5 该远期合约多头的远期价值为：

输入现货价格，交割价格，利率和剩余时间（月数）,输出其远期价值

提示：math库中计算e指数的函数是exp(n)

s=eval(input("现货价格"))
k=eval(input("远期价格"))
r=eval(input("利率"))
t=eval(input("剩余时间"))import math
f = s - k *((math.e)**(-r*t/12))print("远期价值{:.2f}".format(f))

11.小球落下距离和

一个球从100米高处自由落下，每次落地后反跳回原高度的一半，再落下，再反弹。编写一个小程序，求第n次落地时，共经过多少米。

n=eval(input())t = 100
s = 100
for i in range(1,n):t = t / 2s = s + t * 2print("{:.6f}".format(s))

12.计算抛物运动垂直方向位移

抛物运动垂直方向的位移公式

输入速度v 角度a 和时间t（g取9.8 ）计算y（保留两位小数）

import math
v=eval(input())
a=eval(input())
t=eval(input())y = v * math.sin(math.radians(a)) * t - (9.8*t**2) / 2print("{:.2f}".format(y))

13.计算阶乘

n的阶乘公式为

根据该公式输入n 计算n的阶乘（阶乘值四舍五入为整数）

import math
n=int(input())x = (n**n) * (1/(math.e)**n) * ((2*n+1/3)*3.1415926535)**0.5print(round(x))

14.计算分期付款

对于等额分期付款的用户，每月还款金额公式为如图所示。

其中，r月利率，m为贷款金额，n为贷款月数输入r、m和n，计算每月还款金额（保留小数点后两位)

r=eval(input(""))
m=int(input(""))
n=int(input(""))s = r * m / (1-(1+r)**(-n))print("{:.2f}".format(s))

15.计算射程

射程公式如上，输入v和a(角度) 计算x（保留两位小数，重力加速度取9.8)

import math
v=eval(input())
a=eval(input())x = v**2*math.sin(2*math.radians(a))/9.8print("{:.2f}".format(x))

16.计算1到n之间3的倍数的偶数的和（n大于等于3）

n=int(input(""))s = 0
for i in range(3,n+1):if (i%3==0 and i%2==0):s = s + iprint(s)

17.计算1到n之间所有是3的倍数但不是5的倍数的数值之和（n大于等于3）

n=int(input(""))s = 0
for i in range(3,n+1):if i%3==0 and i%5!=0:s = s + iprint(s)

18.计算投资消费每年金额

某用户每年将资金存入银行获取利息收益。年利率为5%。每到年底，用户提取一笔固定的钱作为生活费，再将剩余的资金存入银行。输入年数，本金，提取金额，计算该用户每年剩余的金额。例如，用户输入年数10，本金500000，提取金额20000，注意：保留两位小数

n=eval(input("年数"))
x=eval(input("本金"))
y=eval(input("提取金额"))for i in range(1,n+1):x = x + x * 0.05 - yprint("第{}年金额{:.2f}".format(i,x))

19.房产投资计算

某用户购买一固定资产每年出租获得租金。第一年租金为x，从第二年起每年递增5% 每年底将所有资金存入银行获取利息收益，年利率为y。输入年数n，第一年租金x和年利率y，计算该用户每年金额。例如，用户输入年数5，第一年租金10000，年利率0.02 ，注意：保留两位小数

n=eval(input("年数"))
x=eval(input("第一年租金"))
y=eval(input("年利率"))sum1 = x
print("第{}年金额{:.2f}".format(1,sum1))
for i in range(2,n+1):x = x + x * 0.05sum1 = sum1 + x + (sum1) * yprint("第{}年金额{:.2f}".format(i,sum1))

20.多项式求和

输入a（小于10的整数）和n（项数），计算 a+aa+aaa+aaaa+aaaaa+……（n项）的累加和提示：数列的后一项等于数列的前一项的值乘以10加上a

a=eval(input("输入a"))
n=eval(input("输入n"))s = a
k = a
for i in range(1,n):a = a * 10  +  k s = s + aprint(s)

21.整数数列求和（一）

输入n,计算下列数列和，例如，输入5，输出22.09（平方根使用sqrt函数）

import math
n=eval(input())
s=0
zh=0for i in range(1,n+1):for j in range(1,i+1):zh = zh + math.sqrt(j)print("{:.2f}".format(zh))

22.整数数列求和（二）

输入x和n，求下列数列和，例如输入3和2，输出-0.50

x=eval(input())
n=eval(input())
s=1t = 1
k = 1for i in range(1, n+1):t = t * is = s + x**i / t * kk = k * -1print("{:.2f}".format(s))

23.小乌龟旅行

小乌龟准备去履行，第一天爬行10米，第二天爬行5米，第三天爬行2.5米……以此类推，每天爬行的距离是前一天的一半。输入天数n，计算其累计爬行的距离。例如，输入5，输出共爬行19.375000米输入10，输出共爬行19.980469米

n=eval(input())s = 0
t = 10
for i in range(1,n+1):   s = s + tt = t * 0.5print("共爬行{:.6f}米".format(s))