探索数据结构：顺序栈与链式栈的原理、实现与应用

✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty’s blog

1. 栈的定义

栈简单来说就是一种只允许在一端进行操作(插入与删除）的线性表。即栈是严格遵守后进先出（Last In First Out）的数据结构，简称LIFO结构

img

img

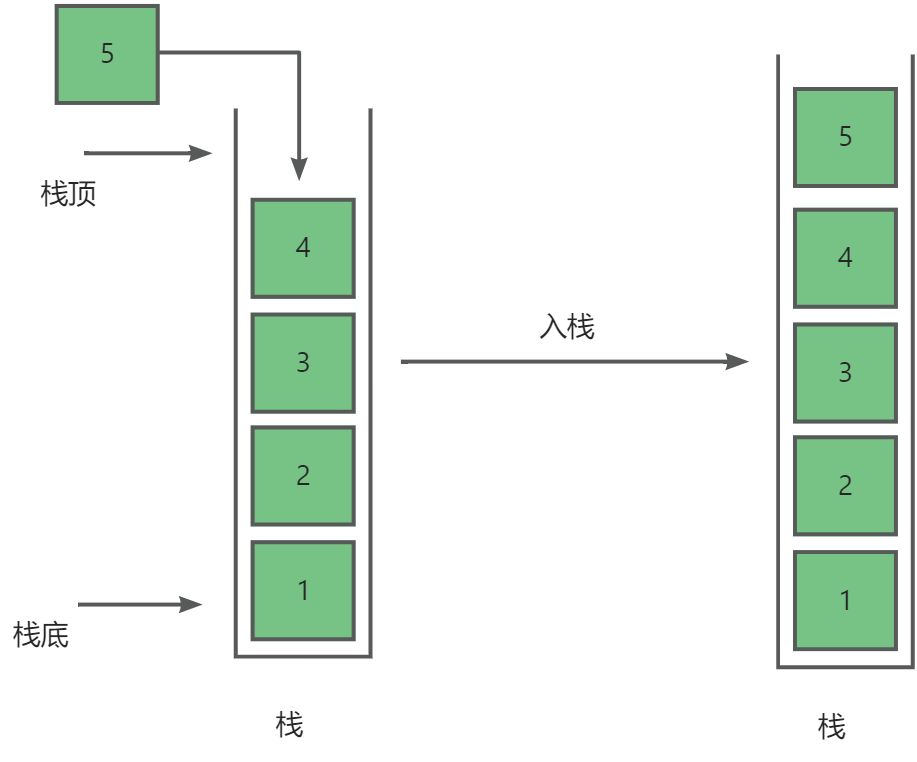
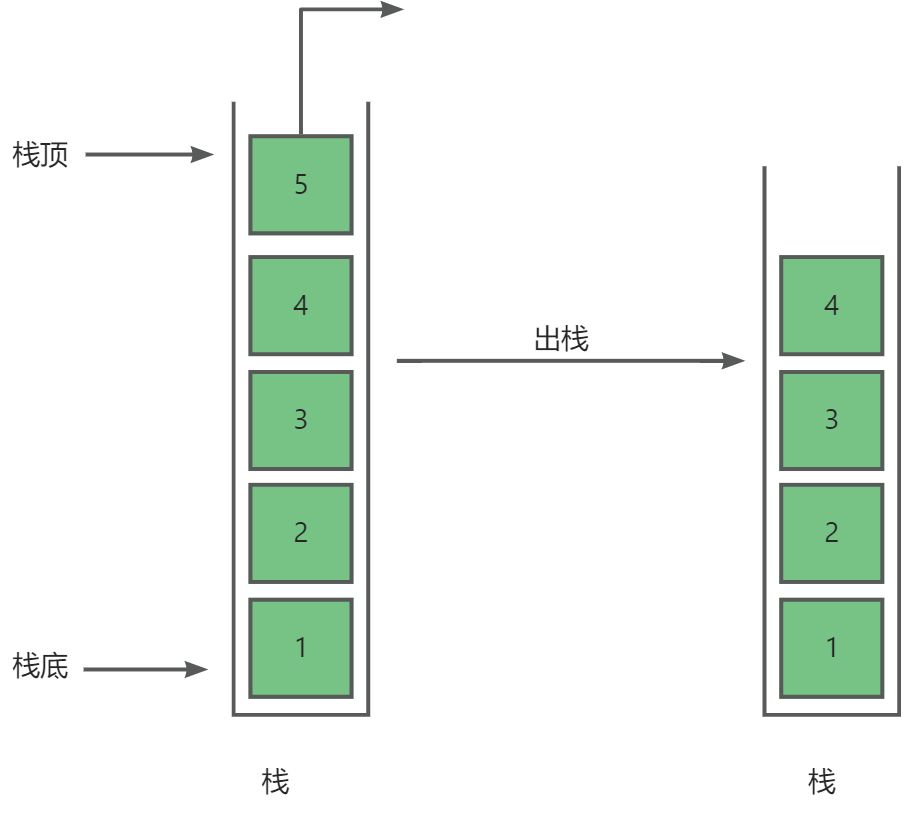
  • 栈顶（Top）：线性表允许进行插入删除的那一端。
  • 栈底（Bottom）：固定的，不允许进行插入和删除的另一端。

2. 栈的分类

当我们了解栈的定义之后，我们就能大概知晓其实现方式无非就是顺序表或者单链表。根据其实现方式，我们又能将栈分为顺序栈与链式栈。

img

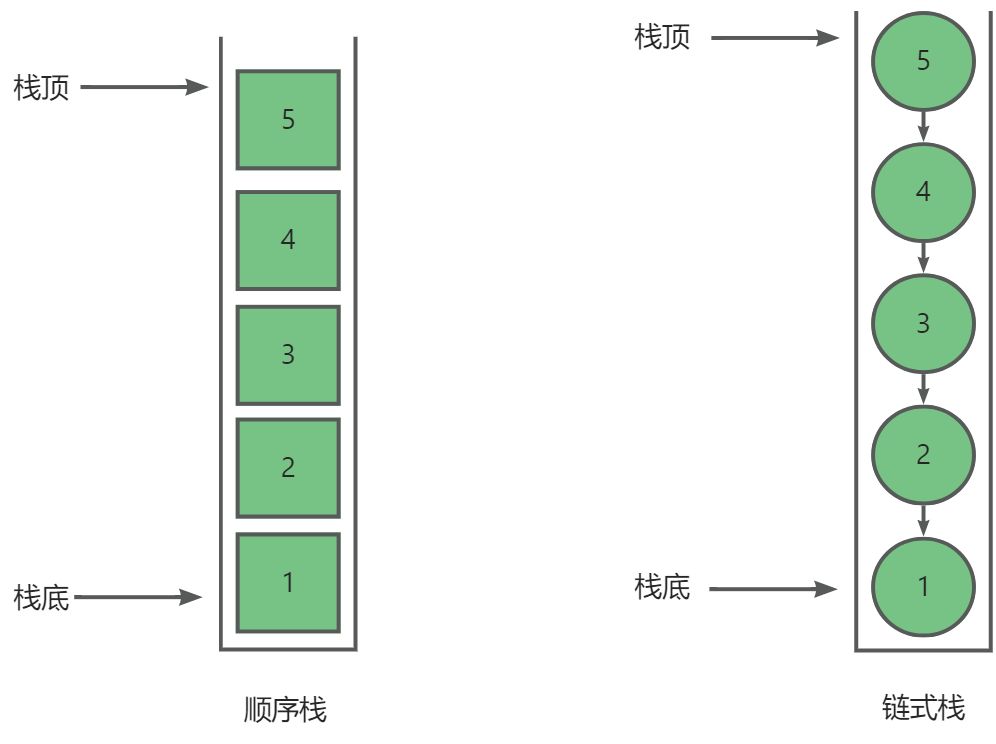
  • 因为单链表头插的效率O(1)明显比尾差O(N)更高，所以我们用单链表实现栈时最好以链表的头为栈顶。如果一定要以尾节点作为栈顶的话，最好以双向链表来实现。本章实现链表栈时以头节点作为栈顶。

3. 栈的功能

  1. 栈的初始化。
  2. 判断栈是否为空。。
  3. 返回栈顶元素。
  4. 返回栈的大小。
  5. 入栈与出栈。
  6. 打印栈的元素。
  7. 销毁栈。

4. 栈的声明

4.1. 顺序栈

顺序栈的声明需要一个指向一块空间的指针a，指向栈顶下一个元素的top，以及标志栈大小的capacity。

typedef int STDataType;
typedef struct Stack 
{STDataType* a;int top;		//栈顶指针int capacity;	//容量
}Stack;
  • 当然也有实现top指向当前栈顶元素的，只不过这时top初始化要为-1，这样才能在填入元素时刚好指向栈顶元素。

4.2. 链式栈

链式栈的声明只需要一个top指针，以及栈的容量capacity。

typedef struct SListNode
{STDataType data;struct SListNode* next;
}SListNode;
typedef struct Stack
{SListNode* top;int size;
}Stack;

5. 栈的功能的具体实现

5.1. 栈的初始化

顺序栈与链式栈的初始化分别与顺序表，链表的初始化大致相同。顺序栈先预先分配一块空间，而链式栈可以先初始为NULL。

5.1.1. 顺序栈
void StackInit(Stack* st)
{assert(st);st->a = (STDataType*)malloc(sizeof(STDataType) * 4);if (st->a == NULL){perror("fail mallic");return;}st->top = 0;st->capacity = 4;
}
5.1.2. 链式栈
void StackInit(Stack* st)
{assert(st);st->top = NULL;st->size = 0;
}
5.1.3. 复杂度分析
  • 时间复杂度：无论是顺序栈还是链式栈花费时间都是一个常数，所以时间复杂度为O(1)。
  • 空间复杂度：无论是顺序栈还是链式栈花费空间都是一个固定大小，所以空间复杂度为O(1)

5.2. 判断栈是否为空

判断栈是否为空只需要判断top的指向。

5.2.1. 顺序栈
bool StackEmpty(Stack* st)
{return (st->top == 0);
}
5.2.2. 链式栈

只需要判断链表头节点下一个是否为空(NULL）。

bool StackEmpty(Stack* st)
{return (st->top == NULL);
}
5.2.3. 复杂度分析
  • 时间复杂度：无论是顺序栈还是链式栈花费判断栈是否为空时间都是一个常数，所以时间复杂度为O(1)。
  • 空间复杂度：无论是顺序栈还是链式栈判断栈是否为空花费空间都是一个固定大小，所以空间复杂度为O(1)。

5.3. 返回栈顶元素

因为不知道top指向的是栈顶还是栈顶的下一个元素，所以为了避免歧义，我们单独实现一个函数来获取栈顶元素。

5.3.1. 顺序栈
STDataType StackTop(Stack* st)
{assert(st);assert(!StackEmpty(st));return st->a[st->top - 1];
}
5.3.2. 链式栈
STDataType StackTop(Stack* st)
{assert(st);assert(!StackEmpty(st));return st->top->data;
}
5.3.3. 复杂度分析
  • 时间复杂度：无论是顺序栈还是链式栈返回栈顶元素花费时间都是一个常数，所以时间复杂度为O(1)。
  • 空间复杂度：无论是顺序栈还是链式栈返回栈顶元素花费空间都是一个固定大小，所以空间复杂度为O(1)

5.4. 返回栈的大小

5.4.1. 顺序栈
int StackSize(Stack* st)
{return st->top;
}
5.4.2. 链式栈
int StackSize(Stack* st)
{return st->size;
}
5.4.3. 复杂度分析
  • 时间复杂度：无论是顺序栈还是链式栈返回栈的大小花费时间都是一个常数，所以时间复杂度为O(1)。
  • 空间复杂度：无论是顺序栈还是链式栈返回栈的大小花费空间都是一个固定大小，所以空间复杂度为O(1)

5.5. 入栈

5.5.1. 顺序栈

顺序栈在入栈之前需要检查栈是否已满。

void STCheckCapacity(Stack* st)
{if (st->top == st->capacity){int newCapacity = st->capacity == 0 ? 4 : st->capacity * 2;STDataType* tmp = (STDataType*)realloc(st->a, newCapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail\n");return ;	}st->a = tmp;st->capacity = newCapacity;}
}
void StackPush(Stack* st, STDataType x)
{assert(st);STCheckCapacity(st);st->a[st->top] = x;st->top++;
}
5.5.2. 链式栈
SListNode* ListCreat(STDataType x)
{SListNode* newnode = (SListNode*)malloc(sizeof(STDataType));if (newnode == NULL){perror("malloc fail");return;}newnode->next = NULL;newnode->data = x;return newnode;
}
void StackPush(Stack* st, STDataType x)
{assert(st);SListNode* newnode = ListCreat(x);if (StackEmpty(st)){st->top = newnode;}else{newnode->next = st->top;st->top = newnode;}st->size++;
}
5.5.3. 复杂度分析
  • 时间复杂度：顺序栈支持下标的随机访问并且我们以单链表的头作为栈顶，所以时间复杂度为O(1)。
  • 空间复杂度：顺序栈插入数据可能会扩容，如果以最坏的情况来算，空间复杂度为O(N)。而链式栈增加的空间为固定大小，所以空间复杂度为O(1)。

5.6. 出栈

5.6.1. 顺序栈
void StackPop(Stack* st)
{assert(st);assert(!StackEmpty(st));st->top--;
}
5.6.2. 链式栈
void StackPop(Stack* st)
{assert(st);assert(!StackEmpty(st));SListNode* next = st->top->next;free(st->top);st->top = next;st->size--;
}
5.6.3. 复杂度分析
  • 时间复杂度：无论是顺序栈还是链式栈出栈花费时间都是一个常数，所以时间复杂度为O(1)。
  • 空间复杂度：无论是顺序栈还是链式栈出栈花费空间都是一个固定大小，所以空间复杂度为O(1)

5.7. 打印栈元素

5.7.1. 顺序栈
void StackPrint(Stack* st)
{assert(st);assert(!StackEmpty(st));for (int i = st->top - 1; i >= 0; i--){printf("%d\n", st->a[i]);}
}
5.7.2. 链式栈
void StackPrint(Stack* st)
{assert(st);assert(!StackEmpty(st));for (SListNode* top = st->top; top!=NULL; top=top->next){printf("%d\n", top->data);}
}
5.7.3. 复杂度分析
  • 时间复杂度：无论是顺序栈还是链式栈打印都需要遍历整个栈，所以时间复杂度为O(N)。
  • 空间复杂度：无论是顺序栈还是链式栈花费空间都是一个固定大小，所以空间复杂度为O(1)

5.8. 销毁栈

5.8.1. 顺序栈
void StackDestroy(Stack* st)
{assert(st);free(st->a);st->a = NULL;st->top = st->capacity = 0;
}
5.8.2. 链式栈
void StackDestroy(Stack* st)
{assert(st);SListNode* top = st->top;while(top!=NULL){SListNode* next = top->next;free(top);top = next;}st->size = 0;
}
5.8.3. 复杂度分析
  • 时间复杂度：无论是顺序栈还是链式栈销毁花费时间都是一个常数，所以时间复杂度为O(1)。
  • 空间复杂度：无论是顺序栈还是链式栈销毁花费空间都是一个固定大小，所以空间复杂度为O(1)

6. 顺序栈与链式栈的对比与应用

6.1. 对比

对比项顺序栈链式栈
时间效率顺序栈支持下标的随机访问，所以时间效率较高，但是这也超出了栈的定义。如果以链表的头作为栈顶，那么链式栈的时间效率也是不错的。但是每次都需要扩容操作，所以效率略比顺序栈低
空间效率顺序栈的扩容较大可能会造成空间的浪费，但是扩容发生的概率低，平均效率还是较高的。链式栈是按需扩容，所以不会造成空间的浪费，但是定义链表节点需要额外定义指针，所以链表节点占用空间更大

6.2. 应用

栈在我们计算机领域应用广泛，如

  1. 当我们打开网页，将多个页面关闭时，这几个页面也就进入栈中。当我们多次点击返回时，就会依次出栈。
  2. 在我们程序设计中，每次调用一个函数时，都会进入一个栈中。当这个函数结束时，这个函数就会出栈。这个知识点我们将会在C语言中详细阐述。

7. 完整代码

7.1. 顺序栈

7.1.1. stack.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include<stdbool.h>
typedef int STDataType;
typedef struct Stack 
{STDataType* a;int top;		//栈顶指针int capacity;	//容量
}Stack;
void StackInit(Stack* st);//初始化栈
bool StackEmpty(Stack* st);//判断栈是否为空
STDataType StackTop(Stack* st);//返回栈顶元素
int StackSize(Stack* st);//栈的大小
void StackPush(Stack* st, STDataType x);//入栈
void StackPop(Stack* st);//出栈
void StackPrint(Stack* st);//打印
void StackDestroy(Stack* st);//销毁栈
7.1.2. stack.c
#include"Stack.h"
void STCheckCapacity(Stack* st)
{if (st->top == st->capacity){int newCapacity = st->capacity == 0 ? 4 : st->capacity * 2;STDataType* tmp = (STDataType*)realloc(st->a, newCapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc fail\n");return ;	}st->a = tmp;st->capacity = newCapacity;}
}void StackInit(Stack* st)
{assert(st);st->a = (STDataType*)malloc(sizeof(STDataType) * 4);if (st->a == NULL){perror("fail mallic");return;}st->top = 0;st->capacity = 4;
}
bool StackEmpty(Stack* st)
{return (st->top == 0);
}
STDataType StackTop(Stack* st)
{assert(st);assert(!StackEmpty(st));return st->a[st->top - 1];
}
int StackSize(Stack* st)
{return st->top;
}
void StackPush(Stack* st, STDataType x)
{assert(st);SListNode* newnode = ListCreat(x);st->a[st->top] = x;st->top++;
}
void StackPop(Stack* st)
{assert(st);assert(!StackEmpty(st));st->top--;
}
void StackPrint(Stack* st)
{assert(st);assert(!StackEmpty(st));for (int i = st->top - 1; i >= 0; i--){printf("%d\n", st->a[i]);}
}void StackDestroy(Stack* st)
{assert(st);free(st->a);st->a = NULL;st->top = st->capacity = 0;
}

7.2. 链式栈

7.2.1. stack.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include<stdbool.h>
typedef int STDataType;
typedef struct SListNode
{STDataType data;struct SListNode* next;
}SListNode;
typedef struct Stack
{SListNode* top;int size;
}Stack;
void StackInit(Stack* st);//初始化栈
bool StackEmpty(Stack* st);//判断栈是否为空
STDataType StackTop(Stack* st);//返回栈顶元素
int StackSize(Stack* st);//栈的大小
void StackPush(Stack* st, STDataType x);//入栈
void StackPop(Stack* st);//出栈
void StackPrint(Stack* st);//打印
void StackDestroy(Stack* st);//销毁栈
7.2.2. stack.c
void StackInit(Stack* st)
{assert(st);st->top = NULL;st->size = 0;
}bool StackEmpty(Stack* st)
{return (st->top == NULL);
}
STDataType StackTop(Stack* st)
{assert(st);assert(!StackEmpty(st));return st->top->data;
}
int StackSize(Stack* st)
{return st->size;
}
SListNode* ListCreat(STDataType x)
{SListNode* newnode = (SListNode*)malloc(sizeof(STDataType));if (newnode == NULL){perror("malloc fail");return;}newnode->next = NULL;newnode->data = x;return newnode;
}
void StackPush(Stack* st, STDataType x)
{assert(st);SListNode* newnode = ListCreat(x);if (StackEmpty(st)){st->top = newnode;}else{newnode->next = st->top;st->top = newnode;}st->size++;
}
void StackPop(Stack* st)
{assert(st);assert(!StackEmpty(st));SListNode* next = st->top->next;free(st->top);st->top = next;st->size--;
}
void StackPrint(Stack* st)
{assert(st);assert(!StackEmpty(st));for (SListNode* top = st->top; top!=NULL; top=top->next){printf("%d\n", top->data);}
}void StackDestroy(Stack* st)
{assert(st);SListNode* top = st->top;while(top!=NULL){SListNode* next = top->next;free(top);top = next;}st->size = 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/557528.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

后端返回文件流，前端导出excel

后端返回文件流，前端导出excel

1. 请求 2. 检查接口 3. 导出代码 &#xff08;如果可以导出&#xff0c;且表格为undefined&#xff0c;把new Blob([res]换成new Blob([res.data], 或者在检查后端是不是返回的blob对象&#xff09; ExportWaterEventListPage(data).then(res > {// console.log("导…
阅读更多...
【ubuntu20.04+tensorflow-gpu1.14配置】

【ubuntu20.04+tensorflow-gpu1.14配置】

ubuntu20.04tensorflow-gpu1.14配置 目录0. 版本注意事项说明1. 个人目录下载后配置系统环境变量2. anaconda配置所有环境&#xff08;过程简便&#xff0c;但容易出现不兼容问题&#xff09;3. 验证tensorflow-gpu4. 一些细节 目录 总结出两种方法 个人目录 下载cuda和cudnn…
阅读更多...
Lombok插件的安装和使用说明

Lombok插件的安装和使用说明

什么是Lombok?? Lombok是一个通过注解以达到减少代码的Java库,如通过注解的方式减少get,set方法,构造方法等。 //普通的实体类public class Student {private Integer id;private Integer age;public Integer getId () {return id;}public void setId (Integer id) {this.id …
阅读更多...
Flink GateWay、HiveServer2 和 hive on spark

Flink GateWay、HiveServer2 和 hive on spark

Flink SQL Gateway简介 从官网的资料可以知道Flink SQL Gateway是一个服务&#xff0c;这个服务支持多个客户端并发的从远程提交任务。Flink SQL Gateway使任务的提交、元数据的查询、在线数据分析变得更简单。 Flink SQL Gateway的架构如下图&#xff0c;它由插件化的Endpoi…
阅读更多...
痛失offer的八股

痛失offer的八股

java面试八股 mysql篇&#xff1a; 事物的性质&#xff1a; 事物的性质有acid四特性。 a&#xff1a;automic&#xff0c;原子性&#xff0c;要么全部成功&#xff0c;要么全部失败&#xff0c;mysql的undolog&#xff0c;事物在执行的时候&#xff0c;mysql会进行一个快照读…
阅读更多...
tcp seq ack

tcp seq ack

seq&#xff08;Sequence Number&#xff09;&#xff1a;32bits&#xff0c;表示这个tcp包的序列号。tcp协议拼凑接收到的数据包时&#xff0c;根据seq来确定顺序&#xff0c;并且能够确定是否有数据包丢失。 ack&#xff08;Acknowledgment Number&#xff09;&#xff1a;3…
阅读更多...
官宣｜阿里巴巴捐赠的 Flink CDC 项目正式加入 Apache 基金会

官宣｜阿里巴巴捐赠的 Flink CDC 项目正式加入 Apache 基金会

摘要&#xff1a;本文整理自阿里云开源大数据平台徐榜江 (雪尽)&#xff0c;关于阿里巴巴捐赠的 Flink CDC 项目正式加入 Apache 基金会&#xff0c;内容主要分为以下四部分&#xff1a; 1、Flink CDC 新仓库&#xff0c;新流程 2、Flink CDC 新定位&#xff0c;新玩法 3、Flin…
阅读更多...
【论文阅读】Scalable Diffusion Models with Transformers

【论文阅读】Scalable Diffusion Models with Transformers

DiT&#xff1a;基于transformer架构的扩散模型。 paper&#xff1a;[2212.09748] Scalable Diffusion Models with Transformers (arxiv.org) code&#xff1a;facebookresearch/DiT: Official PyTorch Implementation of "Scalable Diffusion Models with Transformer…
阅读更多...
计算机组成原理 双端口存储器原理实验

计算机组成原理 双端口存储器原理实验

一、实验目的 1、了解双端口静态随机存储器IDT7132的工作特性及使用方法 2、了解半导体存储器怎样存储和读出数据 3、了解双端口存储器怎样并行读写&#xff0c;产生冲突的情况如何 二、实验任务 (1)按图7所示&#xff0c;将有关控制信号和和二进制开关对应接好&#xff0c;…
阅读更多...
smpl渲染工具

smpl渲染工具

根据3d姿态预测smpl参数 GitHub - Jeff-sjtu/HybrIK: Official code of "HybrIK: A Hybrid Analytical-Neural Inverse Kinematics Solution for 3D Human Pose and Shape Estimation", CVPR 2021 GitHub - woo1/Texture_visualize_smpl: smpl texture visualizatio…
阅读更多...
嵌入式驱动学习第四周——设备树

嵌入式驱动学习第四周——设备树

前言 掌握设备树是 Linux 驱动开发人员必备的技能&#xff01;因为在新版本的 Linux 中&#xff0c;ARM 相关的驱动全部采用了设备树。本篇博客重点介绍一下设备树与设备树语法。 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程&#xff0c;未来预计四个月将高强度更新本…
阅读更多...
探索 PostgreSQL 的外部数据包装器和统计函数

探索 PostgreSQL 的外部数据包装器和统计函数

PostgreSQL 因其稳定性和可扩展性而广受青睐&#xff0c;为开发人员和数据管理员提供了许多有用的函数。在这些函数中&#xff0c;file_fdw_handler、file_fdw_validator、pg_stat_statements、pg_stat_statements_info 以及 pg_stat_statements_reset 是其中的重要函数&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023