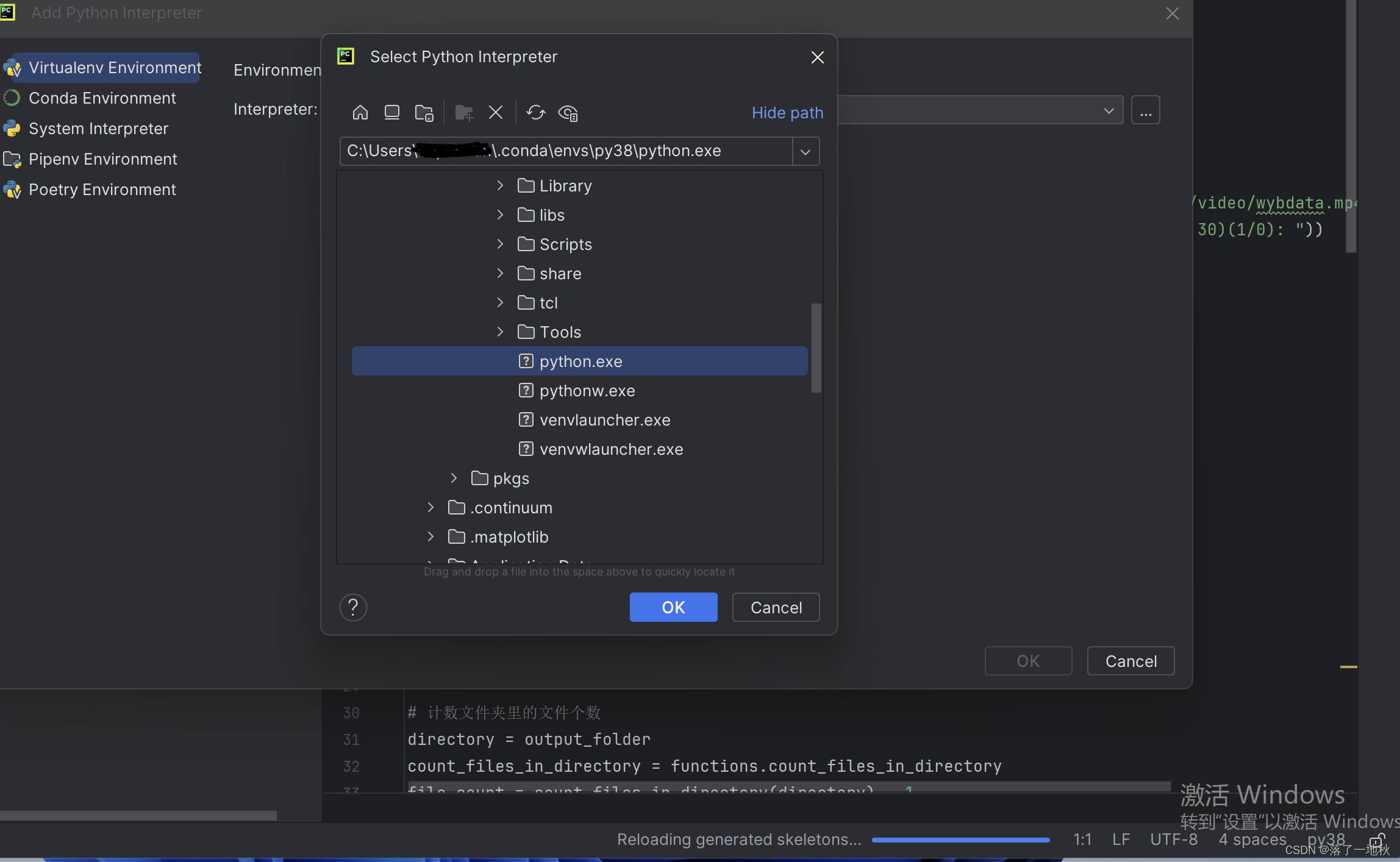
3.22

hw机试【双指针】

Leetcode674 最长连续递增序列

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

双指针

1. 一个慢指针一个快指针

2. 慢指针记录递增子序列起点，快指针去寻找还在当前递增子序列的最后一个数

 class Solution {public int findLengthOfLCIS(int[] nums) {if(nums.length == 1) return 1;int slow = 0;int maxDeep = 0;int tempDeep = 1;for(int fast = 1; fast < nums.length; fast++){if(nums[fast] > nums[fast - 1]){tempDeep++;}else{slow = fast;tempDeep = 1;}maxDeep = Math.max(maxDeep,tempDeep);}return maxDeep;}}

 class Solution {public int findLengthOfLCIS(int[] nums) {int ans = 0;int n = nums.length;int start = 0;for (int i = 0; i < n; i++) {if (i > 0 && nums[i] <= nums[i - 1]) {start = i;}ans = Math.max(ans, i - start + 1);}return ans;}}

NC17 最长回文子串

最长回文子串牛客题霸牛客网 (nowcoder.com)

对于长度为n的一个字符串A（仅包含数字，大小写英文字母），请设计一个高效算法，计算其中最长回文子串的长度。

输入："ababc"

返回值：3

说明：最长的回文子串为"aba"与"bab"，长度都为3

贪心

• step 1：遍历字符串每个字符。

• step 2：以每次遍历到的字符为中心（分奇数长度和偶数长度两种情况），不断向两边扩展。

• step 3：如果两边都是相同的就是回文，不断扩大到最大长度即是以这个字符（或偶数两个）为中心的最长回文子串。

• step 4：我们比较完每个字符为中心的最长回文子串，取最大值即可。

import java.util.*;​public class Solution {// 获取最长回文子串的方法public int getLongestPalindrome(String A) {// 初始最长回文子串长度为1，因为任何单个字符都是回文串int max = 1;// 遍历字符串，查找以当前字符为中心的回文子串for (int i = 0; i < A.length() - 1; i++) {// 更新最长回文子串长度，分别以当前字符及相邻字符为中心查找max = Math.max(max, Math.max(getNum(A, i, i), getNum(A, i, i + 1)));}return max;}​// 查找以指定位置为中心的回文子串的长度private int getNum(String s, int start, int end) {// 从指定位置向两端扩展，直到不再构成回文串while (start >= 0 && end < s.length() && s.charAt(start) == s.charAt(end)) {start--; // 向左移动指针end++;   // 向右移动指针}// 返回回文子串的长度，注意要减去1，因为start和end之间的距离包含了回文子串本身return end - start - 1;}}

• 时间复杂度：O n2

• 空间复杂度：O 1，常数级变量，无额外辅助空间

动态规划

解题思路：

维护一个布尔型的二维数组dp，dp[i][j]表示 i 到 j 的子串是否是回文子串

每次先判断边界字符是否相等，再取决于上个状态的判断结果

算法流程：

• 维护一个布尔型的二维数组dp，dp[i][j]表示 i 到 j 的子串是否是回文子串

• 从长度0到字符串长度n进行判断

• 选定起始下标 i 和终止下标 j， i 和 j 分别为要比较的字符串的左右边界指针

• 从左右边界字符开始判断，即 A.charAt(i) == A.charAt(j)

  • 当相等时，还要判断当前长度 c 是否大于1，不大于则表明只有两个字符的字符串，一个或两个字符肯定是回文串，如“11”

  • 判断的长度大于1时，因为最左右的字符已经相等，因此取决于上一次的子串是否是回文子串, 如 “12121”

• 更新回文串的最大长度

 import java.util.*;public class Solution {public int getLongestPalindrome(String A){// 初始化最长回文子串的长度为0int max = 0;// 获取字符串A的长度int n = A.length();// 创建一个二维布尔数组dp，用于记录字符串的某个子串是否为回文子串boolean[][] dp = new boolean[n][n];// 外层循环：遍历所有可能的子串长度for(int c = 0; c < n + 1; c++){// 内层循环：遍历字符串A，尝试找到所有长度为c的子串for(int i = 0; i < n - c; i++){// 计算当前子串的结束索引int j = i + c;// 判断当前子串的首尾字符是否相等if(A.charAt(i) == A.charAt(j)){// 如果子串长度为1或2，并且首尾字符相等，则标记为回文子串if(c <= 1){dp[i][j] = true;// 如果子串长度大于2，需要进一步判断去掉首尾字符后的子串是否为回文子串}else{dp[i][j] = dp[i+1][j-1];}}// 如果当前子串被标记为回文子串，则更新最长回文子串的长度if(dp[i][j]) max = c + 1;}}// 返回最长回文子串的长度return max;}}

想象一下，你有一串珍珠，每颗珍珠上都刻有一个字母，珍珠串代表给定的字符串。你的任务是找出这串珍珠中最长的那部分，使得从左边开始看和从右边开始看都是一样的顺序（即回文，如“level”或“radar”）。为了完成这个任务，你决定使用一个特殊的放大镜，这个放大镜可以覆盖珍珠串的任意一段，并且立即告诉你这一段是否是回文。

1. 初始化：你决定使用一个表格（二维数组dp）来记录每一段珍珠（子串）是否是回文。表格的行和列代表珍珠串的起始和结束位置，如果某一段是回文，相应的格子就标记为真（true）。

2. 寻找回文：你从珍珠串的一端开始，逐渐增加你检查的珍珠数量（这由变量c表示，它代表当前检查的子串长度减去1）。对于每一段可能的珍珠组合，你使用放大镜来检查：

   • 如果这段珍珠的两端字母相同，那么这可能是一个回文段。但是，要确认它确实是回文，还需要满足以下条件之一：

     • 这段珍珠非常短，长度为1或2，这意味着它们自动构成回文。

     • 如果这段珍珠更长，那么去掉两端的珍珠后，剩下的部分也必须是回文（即dp[i+1][j-1]是true）。

3. 更新最大回文长度：每次你发现一个新的回文段时，你会检查它的长度是否比你之前找到的任何回文段都要长。如果是，你就更新你记录的最大长度。

4. 返回结果：经过整个珍珠串的检查后，你将找到的最长回文段的长度作为结果返回。

这个过程就像是用一个智能放大镜在一串珍珠上寻找隐藏的宝藏，你要找到最长的那段，无论从哪头看都一样美丽的宝藏（回文）。

---

**dp[i+1][j-1]以及为什么它不会导致i+1 > j-1的情况。**

在代码的循环结构中，我们是从较短的子串开始检查的，逐步扩展到较长的子串。这意味着，当我们在查看dp[i][j]时，其基于的较短子串（即dp[i+1][j-1]）已经被检查过并赋值了。这是动态规划的一种常见策略，即解决小问题以帮助解决大问题。

现在，关于i+1 > j-1的疑问，让我们仔细看看for循环的控制变量c。

• c代表当前子串的长度减1。因此，当c = 2时，我们实际上是在处理长度为3的子串。

• 对于长度为3（即c = 2）的子串，i+1至j-1之间实际上没有空间，但因为我们是在检查首尾字符是否相同，所以这个条件在逻辑上是不需要考虑的。换句话说，对于长度为3的子串，dp[i+1][j-1]实际上是在检查一个单字符子串，它默认为真（因为我们在初始化dp数组时没有显式地处理这种情况，但这符合回文的定义）。

对于i+1 > j-1的担忧，这在循环的结构中是被自然避免的。我们从长度为1的子串开始检查，并且逐步增加长度。对于每个子串，我们都是基于已经计算好的更短子串的结果。当c较小时，我们不需要检查dp[i+1][j-1]，因为子串太短，不能构成长度大于3的子串。只有当子串长度至少为3时（即c >= 2），i+1 <= j-1的情况才会出现，并且这时dp[i+1][j-1]的值已经在之前的步骤中被确定了。

---

如何保证max每次都被赋值时是最大的？

代码中的逻辑是遍历所有可能的子串，并且每次找到一个回文子串时，就更新max的值。关键点在于我们是按照子串长度从小到大进行遍历的。这意味着，当我们更新max时，我们已经考虑了所有更短的子串。因为c代表的是当前子串结束索引和开始索引的差值，所以c + 1实际上代表的是子串的长度。每次我们发现一个新的回文子串时，都会检查这个子串的长度，并且只有当它比所有之前发现的回文子串的长度都要长时，才会更新max的值。

NC28 最小覆盖子串

最小覆盖子串__牛客网 (nowcoder.com)

最小覆盖子串 (Minimum Window Substring) - 力扣 (LeetCode)

1. 使用HashMap来统计字符串t中各字符的数量。

2. 使用两个指针表示滑动窗口的左边界和右边界。

3. 扩展右边界直到窗口包含了t中的所有字符。

4. 然后逐步移动左边界以缩小窗口，同时更新最小覆盖子串的长度和起始位置。

5. 注意处理字符计数和检查当前窗口是否覆盖了t中的所有字符。

   1. 如果全部数量满足

   2. 判断是否更新最小子串

      // 更新最小子串 if (ans[0] == -1 || r - l + 1 < ans[0]) {

   3. 移动left

   4. 移动right

import java.util.HashMap;import java.util.Map;​class Solution {public String minWindow(String s, String t) {// 如果s的长度小于t，则直接返回空字符串，因为s中不可能包含tif (s.length() < t.length()) return "";// 用于统计t中各字符的数量Map<Character, Integer> map = new HashMap<>();for(char c: t.toCharArray()) {map.put(c, map.getOrDefault(c, 0) + 1);}// required表示需要找到的唯一字符的数量int required = map.size();// formed用于跟踪当前窗口中满足要求的唯一字符的数量int formed = 0;// 用于跟踪当前窗口中各字符的数量Map<Character, Integer> windowCounts = new HashMap<>();// ans数组用于存储最小覆盖子串的长度和起始位置int[] ans = {-1, 0, 0}; // {window length, left, right}// l和r分别代表滑动窗口的左右边界int l = 0, r = 0;// 开始遍历swhile (r < s.length()) {char c = s.charAt(r);// 更新当前字符c在窗口中的数量windowCounts.put(c, windowCounts.getOrDefault(c, 0) + 1);// 如果当前字符c是t中的字符，并且在窗口中的数量达到了t中的数量，则增加formedif (map.containsKey(c) && windowCounts.get(c).intValue() == map.get(c).intValue()) {formed++;}// 当窗口包含了所有t中的字符时，尝试缩小窗口以找到最小覆盖子串while (l <= r && formed == required) {c = s.charAt(l);// 更新最小覆盖子串的信息if (ans[0] == -1 || r - l + 1 < ans[0]) {ans[0] = r - l + 1;ans[1] = l;ans[2] = r;}// 尝试移除左边界的字符，并更新窗口中的字符计数windowCounts.put(c, windowCounts.get(c) - 1);// 如果移除后导致某个必需的字符不再满足t中的要求，则减少formedif (map.containsKey(c) && windowCounts.get(c) < map.get(c)) {formed--;}// 缩小窗口l++;}// 扩大窗口r++;}// 根据ans数组返回最小覆盖子串，如果ans[0]为-1，则返回空字符串return ans[0] == -1 ? "" : s.substring(ans[1], ans[2] + 1);}}

hw机试【深度搜索】

HJ41 称砝码

递归

• weightSet.addAll(toAdd);

  • add(E e)：这个方法用于向集合中添加单个元素e。如果此集合因调用而改变（即，添加了一个新元素），则返回true；如果这个元素已经存在于集合中，则不会添加，返回false。

  • addAll(Collection<? extends E> c)：这个方法用于将参数集合c中的所有元素添加到当前集合中。如果当前集合因调用而改变，则返回true；如果指定集合中的所有元素都已经存在于当前集合中（即，没有添加任何新元素），则返回false。

•  for(int i = 0; i < m.length; i++){// 对每种砝码重量都遍历一遍​// 设置一个待加和的集合，也就是没统计到全部砝码，每统计一种砝码重量，就把可能的重量加和都放里面List<Integer> toAdd = new ArrayList<>();​// 对于当前砝码重量种类，要加上此前的砝码重量的 重量 组合，而之前的就已经放在set里面了// 所以，要计算当前种类的砝码，要遍历之前每种可能的重量for(int existingWeight: set){​// 添加遍历一种砝码重量的，所有数量构成的加和可能for(int j = 0; j <= x[i]; j++){

import java.util.*;​public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);while(in.hasNext()){int n = in.nextInt(); // 砝码种数int[] weights = new int[n]; // 每种砝码的重量int[] numbers = new int[n]; // 每种砝码的数量for(int i = 0; i < n; i++){weights[i] = in.nextInt();}for(int i = 0; i < n; i++){numbers[i] = in.nextInt();}// 调用动态规划方法System.out.println(countDifferentWeights(weights, numbers));}}private static int countDifferentWeights(int[] weights, int[] numbers) {Set<Integer> weightSet = new HashSet<>();weightSet.add(0); // 初始化，重量0总是可达for (int i = 0; i < weights.length; i++) {List<Integer> toAdd = new ArrayList<>();// 遍历集合中已有的每个重量for (int existingWeight : weightSet) {// 尝试添加0到numbers[i]个当前砝码，计算新的重量for (int j = 1; j <= numbers[i]; j++) {int newWeight = existingWeight + j * weights[i];toAdd.add(newWeight);}}// 将新计算出来的重量加入到集合中weightSet.addAll(toAdd);}return weightSet.size(); // 返回可达重量的数量}}

深度搜索（会超时）

 import java.util.*;​public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);while(in.hasNext()){int n = in.nextInt(); // 砝码的种数int[] m = new int[n]; // 每种砝码的重量int[] x = new int[n]; // 每种砝码对应的数量for(int i = 0; i < n; i++){m[i] = in.nextInt();}for(int i = 0; i < n; i++){x[i] = in.nextInt();}​Set<Integer> set = new HashSet<>();// 初始调用深度优先搜索，参数：当前考察的砝码索引0、当前总重量0、砝码重量数组、砝码数量数组、记录重量的集合dfs(0, 0, m, x, set);​System.out.println(set.size()); // 可称出的不同重量数}}​/*** 深度优先搜索函数* @param i 当前考察的砝码索引* @param sum 当前总重量* @param m 砝码重量数组* @param x 砝码数量数组* @param set 记录已经出现过的总重量*/private static void dfs(int i, int sum, int[] m, int[] x, Set<Integer> set) {// 当所有砝码都考察完时，将当前总重量加入集合if (i == m.length) {set.add(sum);return;}// 对于每种砝码，可以选择0到x[i]个for (int j = 0; j <= x[i]; j++) {// 递归调用，考察下一种砝码，总重量增加j个当前砝码的重量dfs(i + 1, sum + j * m[i], m, x, set);}}}​

---

二叉树

翻转二叉树

代码随想录 (programmercarl.com)

注意只要把每一个节点的左右孩子翻转一下，就可以达到整体翻转的效果

这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！建议拿纸画一画，就理解了

那么层序遍历可以不可以呢？依然可以的！只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的！

递归

1. 传入节点指针

2. 当 root == null

3. left -> temp; right -> left; temp -> right

class Solution {public TreeNode invertTree(TreeNode root) {// 基本情况：如果当前节点为空，则直接返回null。// 这是递归的终止条件，防止对null节点进行操作。if(root == null) return null;// 递归调用invertTree函数，先尝试反转当前节点的左子树。invertTree(root.left);// 接着，递归反转当前节点的右子树。invertTree(root.right);// 在左右子树都被反转后，调用change方法交换当前节点的左右子节点。change(root);// 最后，返回当前节点。注意，对于根节点来说，这意味着返回更新后的树的根。return root;}private void change(TreeNode root){  // 临时保存当前节点的左子节点。TreeNode temp = root.left;// 将当前节点的左子节点更新为其右子节点。root.left = root.right;// 最后，将保存的原左子节点赋值给当前节点的右子节点，完成交换。root.right = temp;}}​

BFS 广度优先搜索

• 一定要写这一句 if(root == null) return null;

 class Solution{public TreeNode invertTree(TreeNode root){// 如果根节点为空，则直接返回null，表示没有需要反转的树。if(root == null) return null;// 使用一个双端队列（在这里作为队列使用）来进行层序遍历。Deque<TreeNode> deque = new LinkedList<>();// 将根节点加入队列，作为遍历的起点。deque.offer(root);​// 只要队列不为空，就继续遍历。while(!deque.isEmpty()){// 当前层的节点数量。int size = deque.size();while(size-- > 0){// 从队列中取出一个节点。TreeNode temp = deque.poll();// 交换这个节点的左右子节点。change(temp);// 如果当前节点的左子节点不为空，则将左子节点加入队列。if(temp.left != null) deque.offer(temp.left);// 如果当前节点的右子节点不为空，则将右子节点加入队列。if(temp.right != null) deque.offer(temp.right);}}// 返回反转后的树的根节点。return root;}private void change(TreeNode root){  // 临时保存当前节点的左子节点。TreeNode temp = root.left;// 将当前节点的左子节点更新为其右子节点。root.left = root.right;// 将保存的原左子节点赋给当前节点的右子节点，完成交换。root.right = temp;}}

对称二叉树

给定一个二叉树，检查它是否是镜像对称的。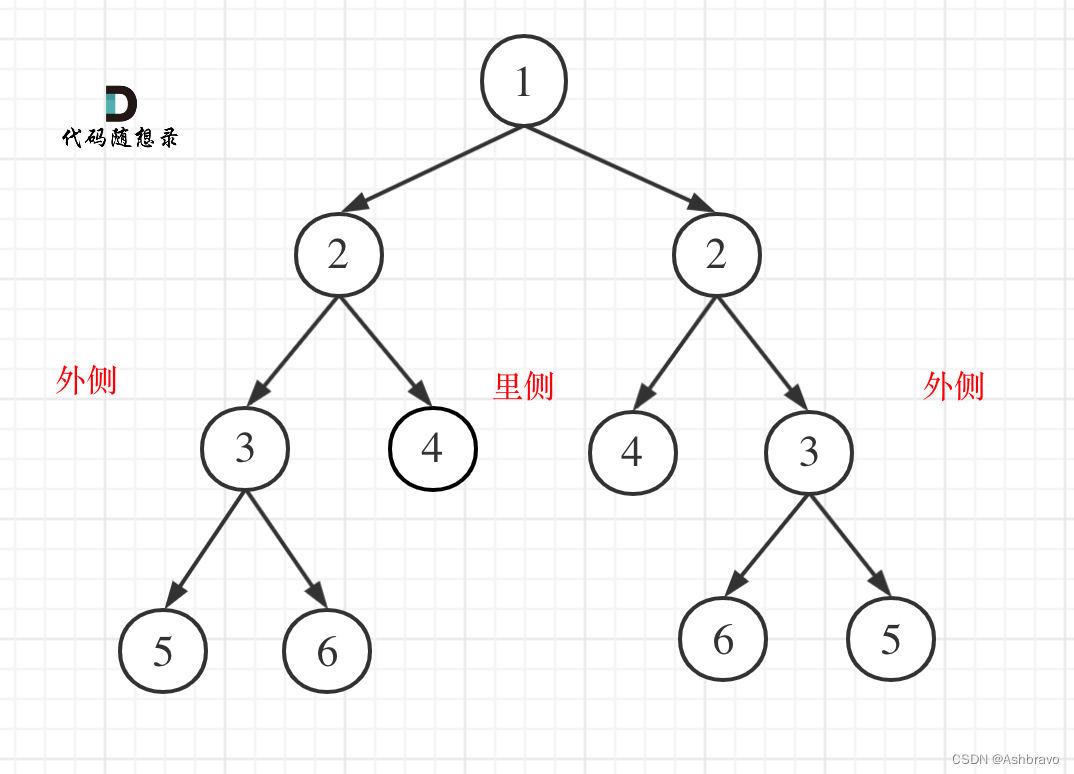

其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。正是因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。

递归三部曲

1. 确定递归函数的参数和返回值

因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。

返回值自然是bool类型。

代码如下：

 bool compare(TreeNode* left, TreeNode* right)

1. 确定终止条件

要比较两个节点数值相不相同，首先要把两个节点为空的情况弄清楚！否则后面比较数值的时候就会操作空指针了。

节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）

• 左节点为空，右节点不为空，不对称，return false

• 左不为空，右为空，不对称 return false

• 左右都为空，对称，返回true

此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：

• 左右都不为空，比较节点数值，不相同就return false

此时左右节点不为空，且数值也不相同的情况我们也处理了。

代码如下：

 if (left == NULL && right != NULL) return false;else if (left != NULL && right == NULL) return false;else if (left == NULL && right == NULL) return true;else if (left->val != right->val) return false; // 注意这里我没有使用else

注意上面最后一种情况，我没有使用else，而是else if， 因为我们把以上情况都排除之后，剩下的就是 左右节点都不为空，且数值相同的情况。

1. 确定单层递归的逻辑

此时才进入单层递归的逻辑，单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

• 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。

• 比较内侧是否对称，传入左节点的右孩子，右节点的左孩子。

• 如果左右都对称就返回true ，有一侧不对称就返回false 。

代码如下：

 bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左bool isSame = outside && inside;                    // 左子树：中、 右子树：中（逻辑处理）return isSame;

如上代码中，我们可以看出使用的遍历方式，左子树左右中，右子树右左中，所以我把这个遍历顺序也称之为“后序遍历”（尽管不是严格的后序遍历）。

递归

 class Solution {public boolean isSymmetric(TreeNode root) {// 如果根节点为空，则树不对称（按照定义空树不是对称的，但实际上空树通常被认为是对称的，这里根据题目要求调整）if(root == null) return true;// 调用比较函数，比较根节点的左子树和右子树return compare(root.left, root.right);}​private boolean compare(TreeNode left, TreeNode right){// 如果左节点为空而右节点不为空，或者左节点不为空而右节点为空，则不对称if(left == null && right != null) return false;if(left != null && right == null) return false;// 如果左右节点都为空，即在对称的位置上都没有子节点，则当前部分对称if(left == null && right == null) return true;// 如果左右节点的值不相同，则不对称if(left.val != right.val) return false;​// 比较外侧：比较左子树的左子节点和右子树的右子节点boolean outcompare = compare(left.left, right.right);// 比较内侧：比较左子树的右子节点和右子树的左子节点boolean incompare = compare(left.right, right.left);​// 只有当外侧和内侧都对称时，当前部分才对称return outcompare && incompare;}}

迭代

这里我们可以使用队列来比较两个树（根节点的左右子树）是否相互翻转，（注意这不是层序遍历）

1. 队列

2. 添加左右

3. 比较

4. 再添加左左，右右，左右，右左

• 注意 while(!deque.isEmpty()){

  if(left == null && right == null) continue; ，因为还要再向下迭代，所以要继续，直到所有都没有不对称

 class Solution{public boolean isSymmetric(TreeNode root){// 如果根节点为null，则树为空，按定义空树是对称的if(root == null) return true;​// 使用一个双端队列（Deque）来支持从两端插入和移除元素，// 但在这里主要作为普通队列使用，用于层序遍历二叉树Deque<TreeNode> deque = new LinkedList<>();​// 将根节点的左右子节点加入队列// 这是检查对称性的起始点deque.offer(root.left);deque.offer(root.right);​// 只要队列不为空，就继续遍历while(!deque.isEmpty()){// 从队列中取出两个节点，分别代表要比较的对称节点TreeNode left = deque.poll();TreeNode right = deque.poll();​// 如果两个节点都为null，说明这一部分是对称的，继续下一轮比较if(left == null && right == null) continue;​// 如果一个节点为null而另一个不为null，说明树不对称，返回falseif(left == null || right == null) return false;​// 如果两个节点的值不相等，也说明树不对称，返回falseif(left.val != right.val) return false;​// 将下一层的对称节点加入队列，以待后续比较// 注意加入队列的顺序，它决定了比较的对称性deque.offer(left.left);deque.offer(right.right);deque.offer(left.right);deque.offer(right.left);}​// 如果遍历完所有节点都符合对称性，说明整棵树是对称的，返回truereturn true;}}